Лекция 1(С.Т.О.). Лекция До сих пор мы предполагали, что источники, приемники и другие тела, относительно которых рассматривается распространение света
 Скачать 0.67 Mb. Скачать 0.67 Mb.
|
|
§6 Релятивистский закон сложения скоростей. Новым релятивистским представлениям о пространстве и времени соответствует новый закон сложения скоростей. Очевидно, что классический закон сложения скоростей не может быть справедлив, так как он противоречит утверждению о постоянстве скорости света в вакууме. Рассмотрим пример: если поезд движется со скоростью Мы получим закон сложения скоростей для частного случая: тело (частица) движется вдоль оси x’ системы отсчета К’, которая в свою очередь, движется со скоростью 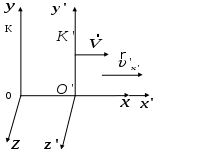 Обозначим скорость частицы в системе К через 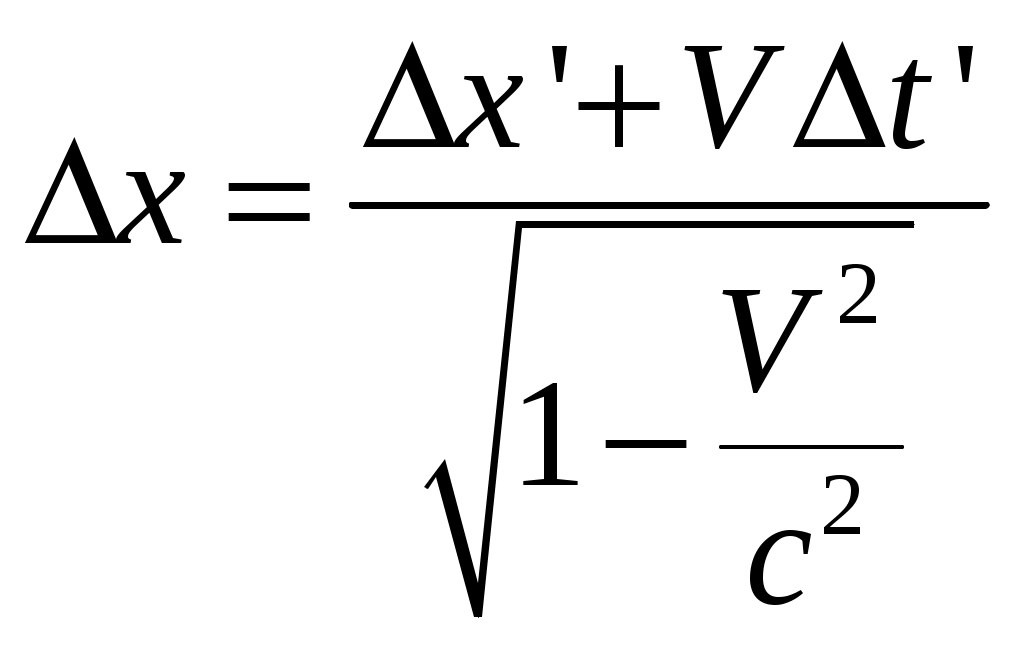 (1) (1)а интервалы 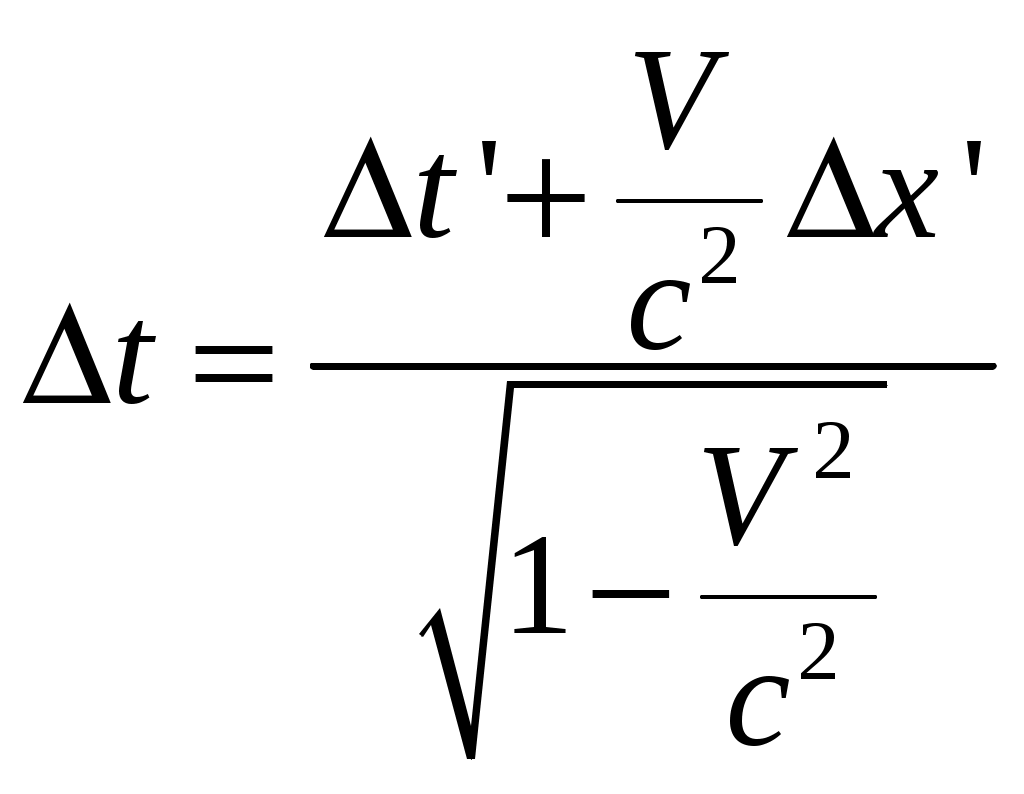 (2 (2Разделив почленно левые и правые части уравнений (1) и (2), получим: 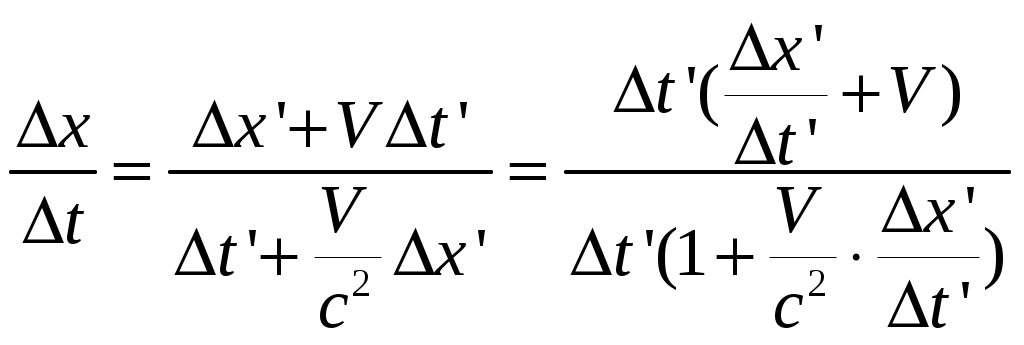 (3) (3)Здесь 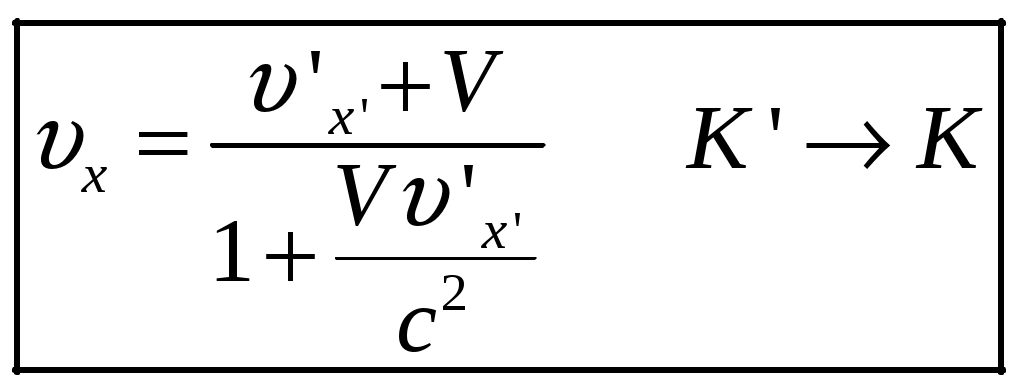 (4) (4)то есть по этой формуле (4) осуществляется преобразование скоростей при переходе от системы К’ к системе К . Воспользовавшись преобразованием Лоренца можно получить формулу для преобразования скоростей от при переходе от системы К к системе К’: 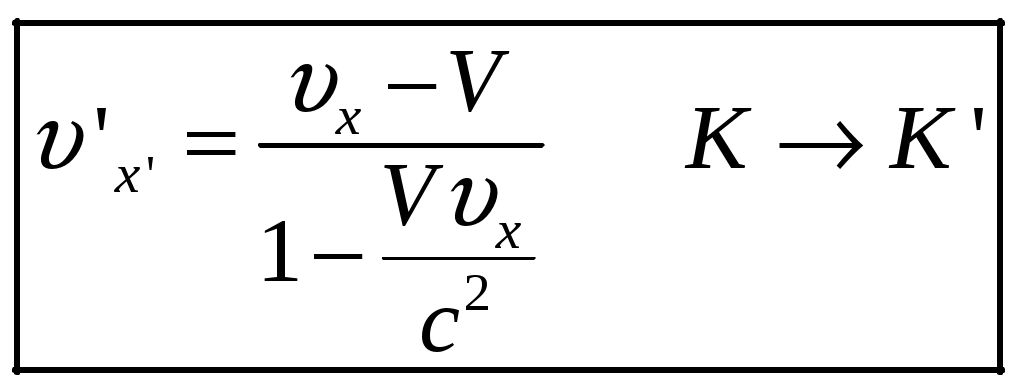 (5) (5)то есть формулы (4) и (5) отличаются только знаком перед V. Анализ этих выражений: 1) Если 2) При 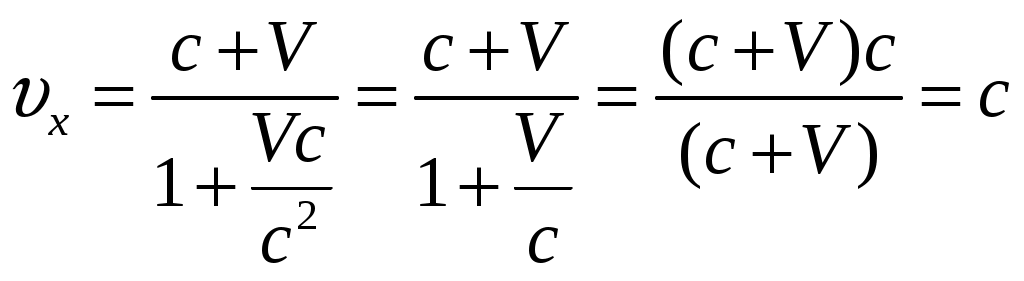 то есть Замечательным свойством релятивистского сложения скоростей (4) является то, что при любых значениях скоростей 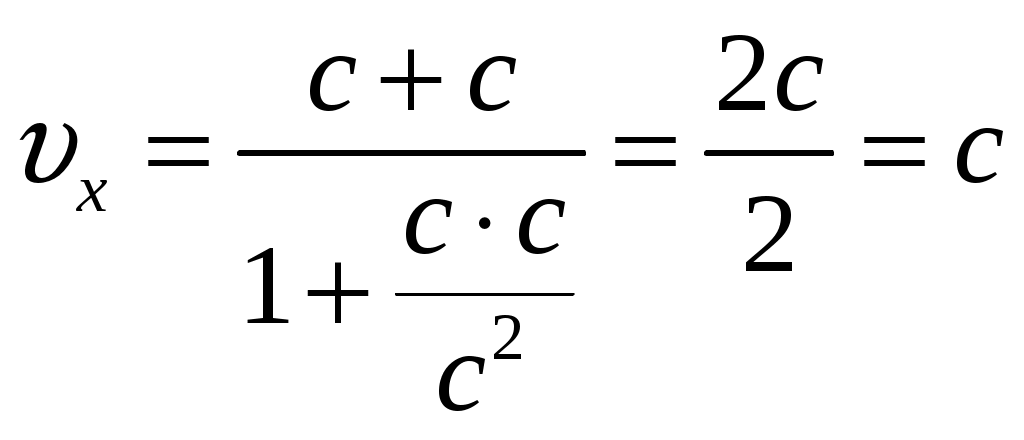 Скорости А теперь выпишем формулы преобразования и сложения скоростей в общем случае: а) в системе К компоненты скорости б) в системе K’ компоненты скорости Используя преобразования Лоренца и произведя соответствующие преобразования, получаем релятивистский закон сложения скоростей: 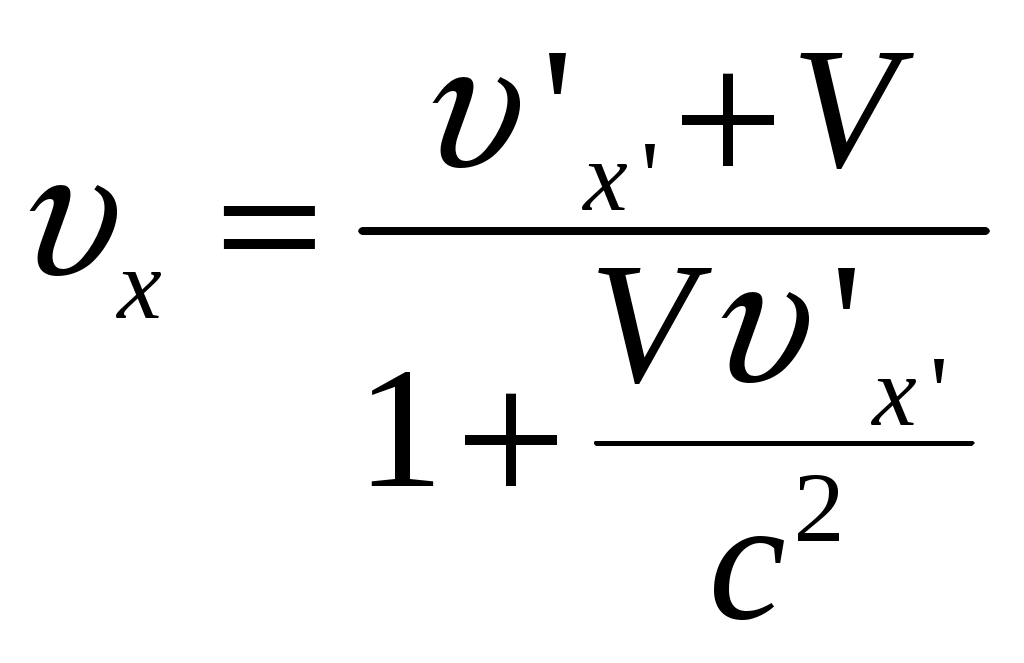 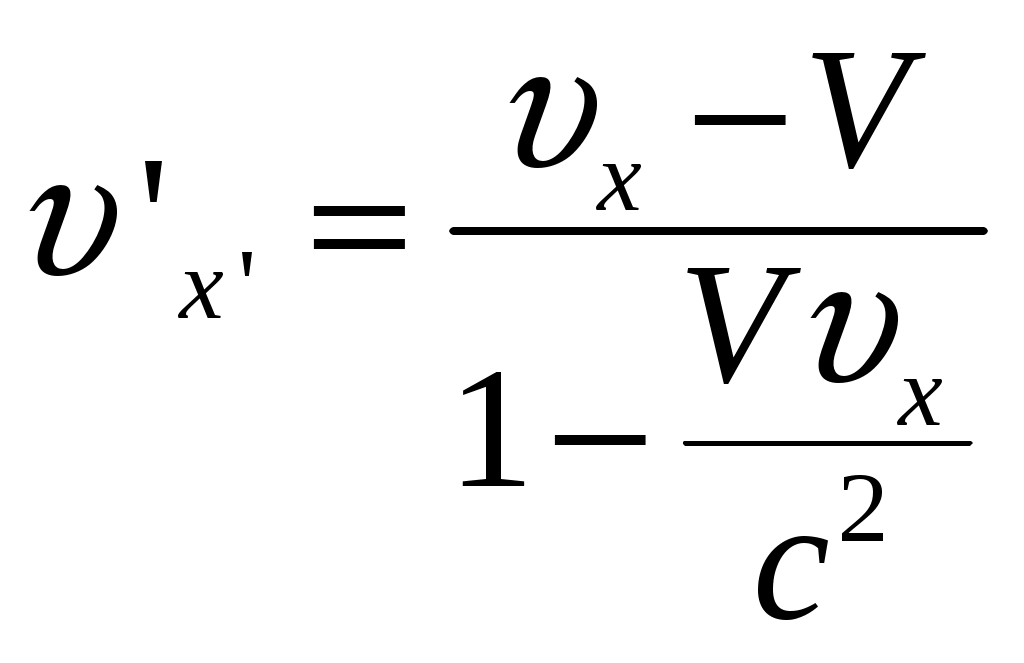 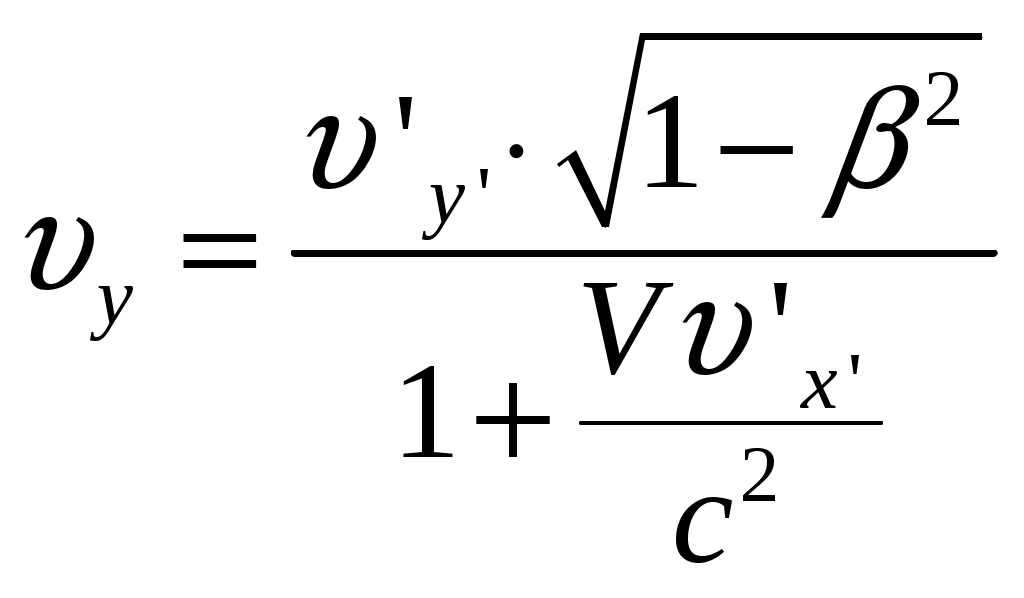 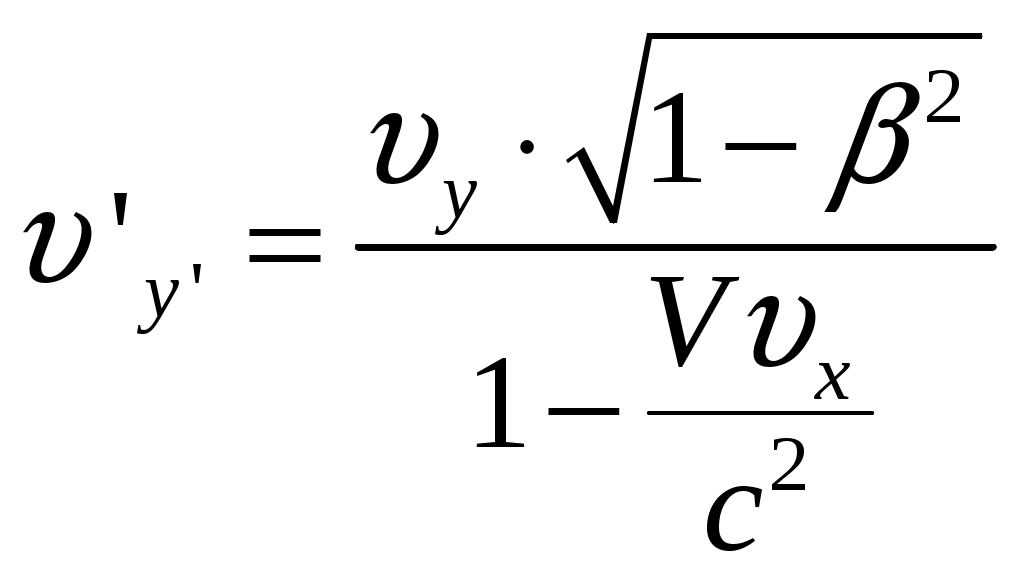 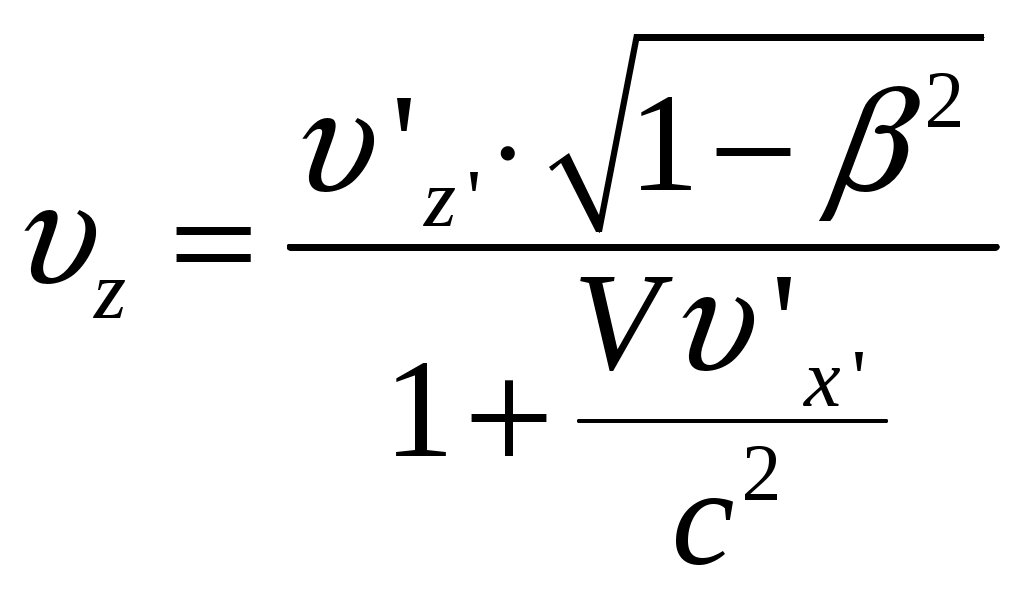 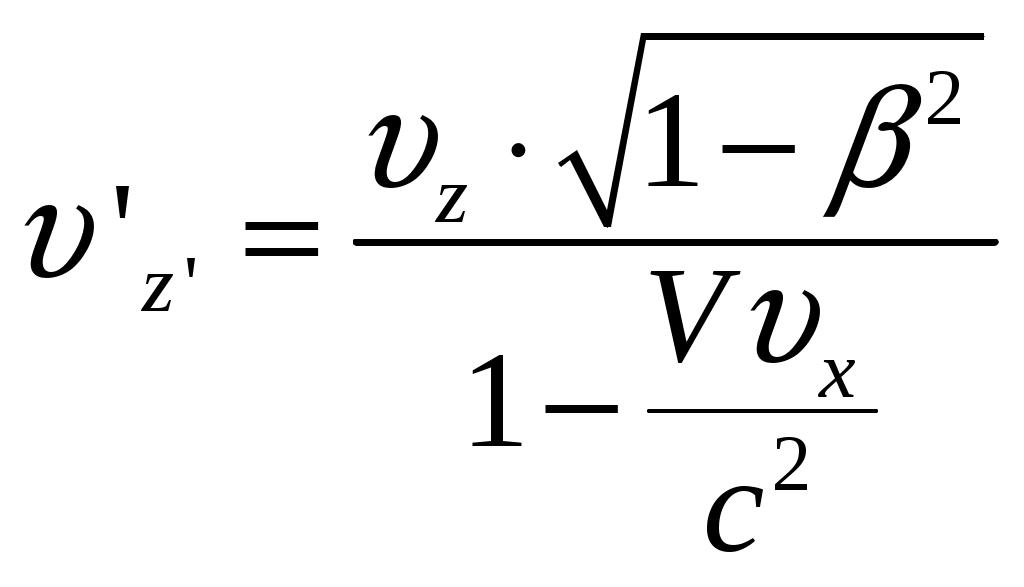 , где , где |
