Лекция 1(С.Т.О.). Лекция До сих пор мы предполагали, что источники, приемники и другие тела, относительно которых рассматривается распространение света
 Скачать 0.67 Mb. Скачать 0.67 Mb.
|
|
Специальная (частная) теория относительности. Лекция 1. До сих пор мы предполагали, что источники, приемники и другие тела, относительно которых рассматривается распространение света, неподвижны. Возникает вопрос - как скажется распространение света движение, например, источника или приемника световых волн. При этом необходимо указать - относительно чего происходит движение! В акустике движение источника и приемника звуковых волн рассматривается относительно среды, в которой эти волны распространяются - например, относительно воздуха. Выяснилось, что такое движение источника и приемника влияет на распространение звуковых волн, на протекание акустических явлений - эффект Доплера - и следовательно может быть обнаружено. А как быть в случае света (электромагнитных волн)? Волновая теория рассматривала распространение света в некой среде, называемой эфиром. Эфир - это особая среда, заполняющая все мировое пространство и пронизывающая все тела. Раз эфир представляет собой некую среду, можно было рассчитывать обнаружить движение тел - например, источников или приемников света - по отношению к этой среде, то есть к эфиру. В частности, следовало ожидать существование «эфирного ветра», обдувающего землю при ее движении вокруг солнца. Обнаружение движения тел относительно эфира привело бы к появлению абсолютной системы отсчета, по отношению к которой можно бы рассматривать движение всех других систем отсчета. §1 Преобразования Галилея. Принцип относительности Галилея. Обратимся к механике Ньютона, которая рассматривает движения тел со скоростями Для простоты выберем оси координат так, как показано на рис. 1. Отсчет времени начнем с того момента времени, когда начала координат O и O’ совпадают. Преобразованиями Галилея - называются преобразования координат и времени, применяемые в ньтоновской механике при переходе от одной инерциальной системы отсчета К (x,y,z) к другой K’ (x’, y’, z’), которая движется поступательно относительно К с постоянной скоростью Первая аксиома утверждает что ход времени (соответственно промежутков времени между какими-либо двумя событиями) одинаков во всех инерциальных системах отсчета. Вторая аксиома - размеры тела не зависят от скорости его движения относительно системы отсчета. Пусть {x, y, z} - координаты точки А в системе К (в момент времени t); {x’, y’, z’} - координаты точки А в системе К’ на ось Если в начальный момент времени (t=t’=0) начала координат О и О’ совпадают, то преобразования Галилея имеют вид: 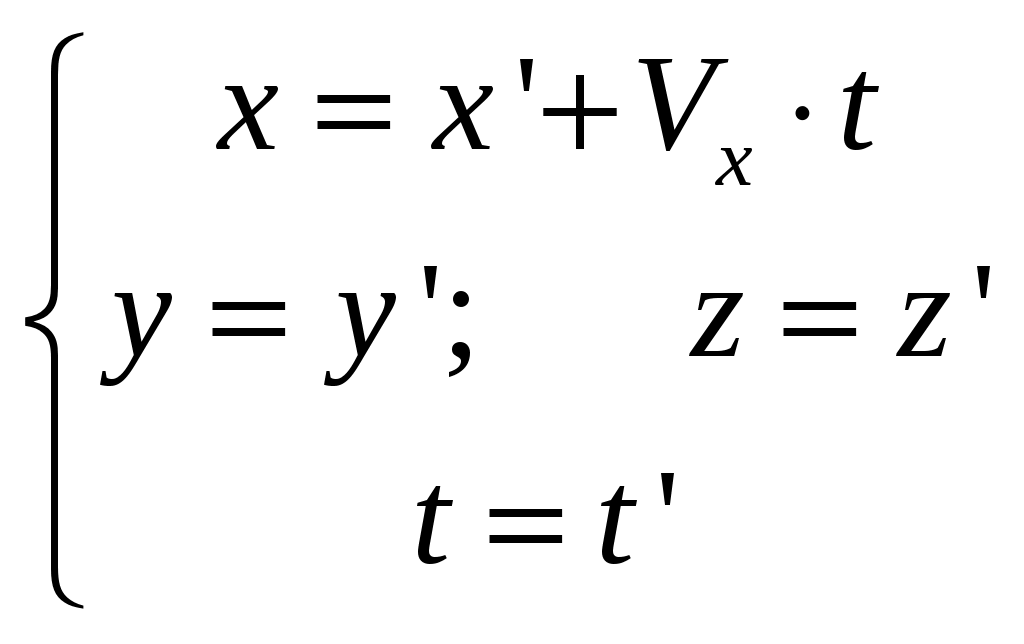 или в общем виде: 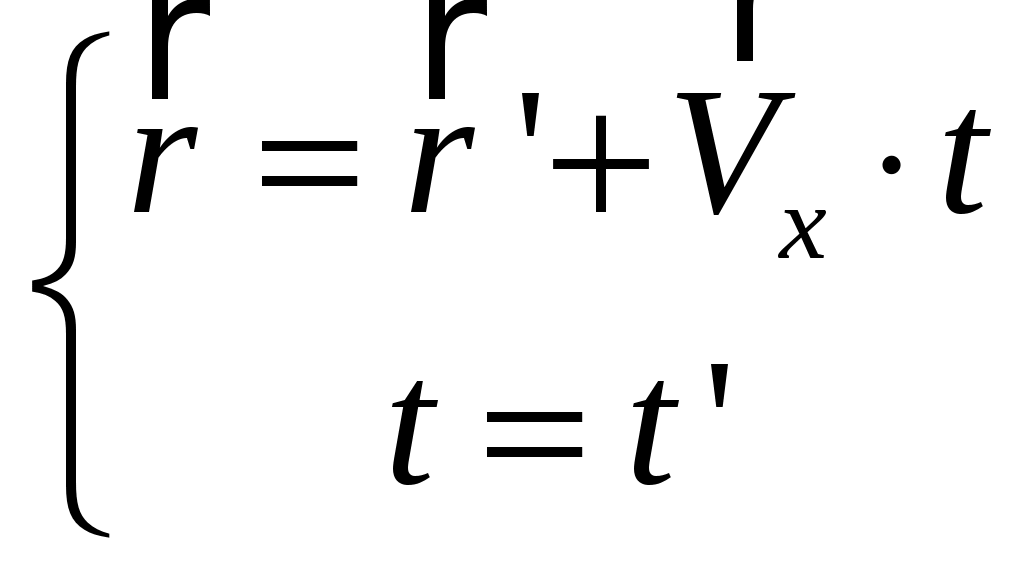 (1) (1)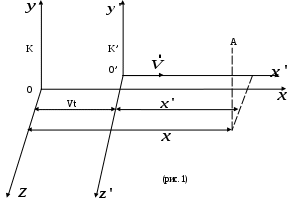 Эти уравнения позволяют перейти от координат и времени одной инерциальной системы отсчета к координатам и времени другой инерциальной системы отсчета. Продифференцировав (1) по времени, получим уравнение 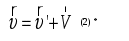 Это уравнение можно рассматривать как формулу преобразования скорости частицы при переходе от системы отсчета К’ к системе К, либо как закон сложения скоростей: скорость частицы относительно системы К (относительно неподвижной системы отсчета) равна сумме Дифференцируя уравнение (2) по времени, получаем (при 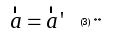 То есть ускорения частицы относительно систем К и К’ одинаковы! * * * Теперь сравним силу (4) То есть эти силы одинаковы. Почему? Это следует из того, что сила зависит от расстояний между данной частицей и взаимодействующими с ней частицами и, может быть, от относительных скоростей частиц. Но из формул преобразования Галилея следует (см. (1) и (2)), что эти величины одинаковы во всех инерциальных системах одинаковы: поэтому одинаковы и силы Масса m так же одинакова во всех системах отсчета. Из сказанного следует, что если выполняется равенство II закона Ньютона в системе К: то будет выполняться и равенство в системе К’: то есть уравнения динамки при переходе от одной инерциальной системы отсчета к другой не изменяется (то есть имеют одинаковую форму записи). Это утверждение называется принципом относительности Галилея: все законы механики одинаково формулируются (имеют одинаковую форму) для всех инерциальных систем отсчета. Галилей первый обратил внимание на то, что никакими механическими опытами, осуществленными в пределах данной ИСО (инерциальной системе отсчета), невозможно установить, находится ли она в состоянии покоя, или в состоянии равномерного прямолинейного движения. Он писал, что в закрытой каюте равномерно движущегося корабля мухи летают с одинаковой скоростью по всем направлениям; расстояние, на которое вы прыгнете, не зависит от направления прыжка; капли из отверстия в дне подвешенного ведерка будут падать так же, как они падали, когда корабль был неподвижен. То есть что бы определить, движется корабль или покоится, надо выглянуть в окно (так как никакие механические опыты не помогают). Все перечисленные процессы являются проявлением принципа относительности. Принцип относительности Галилея свидетельствует о том, что в механике все инерциальные системы отсчета равноправны. Среди них нельзя указать какую-то особую, «главную» инерциальную систему отсчета, по отношению к которой, покой и движение тел можно было бы считать абсолютными (то есть рассматривать, как «абсолютное движение» тел относительно этой «главной» инерциальной системы, так и «абсолютный покой»). Величины , которые имеют одно и то же числовое значение во всех системах отсчета, называются инвариантными (invariantis - неизменяющийся). Примерами таких величин могут служить электрический заряд, скорость света c в вакууме и другие. Введение понятия инвариантных уравнений - это уравнения, вид которых не изменяется по отношению к преобразованию координат и времени при переходе от одной инерциальной системы отсчета к другой. Сами величины, входящие в уравнение, могут меняться при переходе к другой системе отсчета. Однако формулы, выражающие связь между величинами, остаются неизменными. В качестве примера можно привести уравнение теоремы о кинетической энергии частицы (материальной точки) то есть изменение Используя понятие инвариантности, принцип относительности Галилея можем сформулировать так: уравнения механики инвариантны по отношению к преобразованиям Галилея. §2 Опыт Майкельсона. Принцип относительности Галилея касается только механики. По мере развития других разделов физики, в частности оптики и электродинамики, возник естественный вопрос - распространяется ли принцип относительности на другие явления? Если нет, то с помощью этих (немеханических) явлений можно в принципе различить инерциальные системы отсчета и в свою очередь поставить вопрос о существовании главной, или абсолютной, системы отсчета! Одно из таких явлений, которое, как ожидали, по-разному протекает в разных системах отсчет - это распространение света. Согласно господствовавшей в то время волновой теории, световая волна должна распространяться с определенной скоростью по отношению к некоторой гипотетической среде - «светоносному эфиру» (о природе этого эфира не было единого мнения). Далее рассуждали так - «светоносный эфир» не может покоиться во всех инерциальных системах отсчета сразу. Следовательно, выделяется одна из инерциальных систем отсчета - абсолютная - та самая, которая неподвижна относительно «светоносного эфира». Полагали, что только в этой системе отсчета свет распространяется с одинаковой скоростью С во всех направлениях. Далее - если некоторая инерциальная система отсчета движется по отношению к эфиру со скоростью Это предположение оказалось возможным проверить на опыте, который и был осуществлен в 1881 году Майкельсоном и 1887 году Майкельсоном совместно с Морли. Цель этого эксперимента заключалась в том, что бы обнаружить «истинное» движение Земли относительно эфира. Было использовано движение Земли по ее орбите со скоростью 30 км/с. Идея эксперимента состояла в следующем. Свет от источника S посылался в двух взаимно перпендикулярных направлениях, отражается от зеркал A и B, находящихся на одинаковом расстоянии 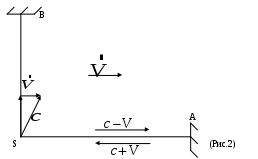 Предположим, что установка вместе с Землей движется так, что ее скорость (I) Если скорость света подчиняется обычному закону скоростей 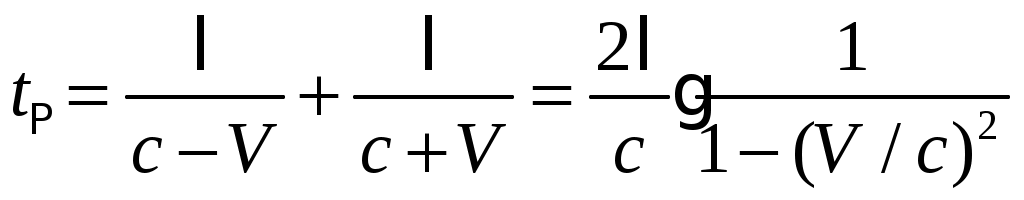 На пути SBS скорость света относительно установки равна 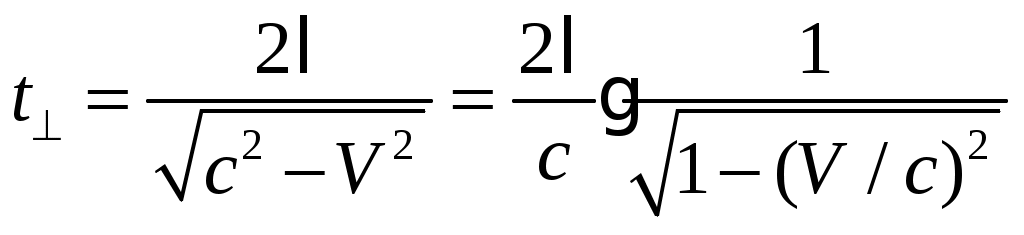 Из сравнения выражений для Несмотря на то, что ожидаемая разность времен была чрезвычайно мала, установка была чувствительной, что бы эту разность надежно обнаружить (это достигалось с помощью очень чувствительного интерференционного метода). Однако результат опыта оказался отрицательным - разность времен не была обнаружена! Опыты проводились не однократно в разное время года, но они не дали ожидаемого результата. Отрицательный результат опыта Майкельсона противоречил тому, что ожидалось на основании преобразований Галилея - преобразования скоростей. Он показал так же, что: 1) нельзя обнаружить движение относительно эфира; 2) скорость света не зависти от движения источника (ведь источник движется по-разному относительно эфира в разные времена года). Поставленные позже другие опыты показали также, что скорость света не зависит от скорости источника! §3 Постулаты специальной теории относительности. Глубокий анализ всего экспериментального и теоретического материала, имевшегося к началу XX века, привел Альберта Эйнштейна к пересмотру исходных положений классической физики, прежде всего представлений о свойствах пространства и времени. В результате чего была создана специальная теория относительности, которая явилась логическим заверением всей классической физики. В основе специальной теории относительности лежат два постулата Эйнштейна. I постулат - принцип относительности Эйнштейна: все законы природы и уравнения, их описывающие, инвариантны, то есть не изменяются при переходе от одной инерциальной системы отсчета к другой. Другими словами: все инерциальные системы отсчета эквивалентны (неразличимы) по своим физическим свойствам. II постулат - принцип инвариантности (независимости) скорости света от скорости источника: скорость света в вакууме одинакова во всех инерциальных системах отсчета и не зависит от движения источников и приемников света. Еще раз обратим внимание, что эти постулаты теории относительности противоречат представлениям о свойствах пространства и времени, которые приняты в классической механике и отражены в преобразованиях Галилея. В частности, это относится к считающемуся в механике Ньютона «само собой разумеющемуся» утверждению об одинаковости хода времени во всех ИСО и, следовательно, об абсолютности промежутка времени между какими-либо двумя событиями. Например, если два события происходят одновременно по часам в одной ИСО, то они, согласно классическим направлениям, совершаются так же одновременно по часам в любой другой инерциальной системе отсчета. Однако, легко убедится в том, что существование предельной скорости приводит к тому, что понятие одновременности, считающееся в ньютоновской механике абсолютным, в действительности является относительным. Рассмотрим следующий пример: пусть мимо неподвижного наблюдателя в К - системе (это покоящаяся ИСО) проносится со скоростью  Однако наблюдатель в неподвижной К - системе не согласится с нашими рассуждениями. С его точки зрения космонавт на носу ракеты удаляется вместе с ракетой от космонавта в центре - и поэтому свет, догоняя его, должен пройти больше половины длины ракеты и достичь этого космонавта позже, чем он достигнет космонавта на корме ракеты, который вместе с ракетой приближается к месту вспышки. Поэтому, что бы достичь космонавта на корме, свету надо пролететь расстояние меньше половины длины ракеты. Вывод: космонавт на корме ракеты должен увидеть вспышку света раньше, чем космонавт на носу! Наблюдатель в неподвижной К - системе отсчета прав - эти два события - момент достижения светом космонавтов на носу и корме ракеты не одновременны! Но правы и космонавты в ракете, то есть в К’ - системе - эти события как раз одновременны! Но это не означает, что существует две истины - истина одна. И вот она: события, одновременны в одной ИСО, неодновременные в другой ИСО, движущейся с иной, чем первая система отсчета скоростью. Другими словами - одновременность пространственно разнесенных событий относительна! |
