5 Геометрические характеристики. Лекция Геометрические характеристики плоских сечений
 Скачать 315.73 Kb.
|
|
Рис. 4.9 По формуле параллельного переноса  , откуда  .Круг Для любых центральных осей  , поэтому  .Как известно, полярный момент инерции круга равен  . Рис. 4.10 Следовательно,  .Кольцо (  ).Момент инерции относительно оси  (рис.4.11) можно определить как разность моментов инерции наружного и внутреннего круга: .Для тонкого кольца существует приближенная формула  , где dср – средний диаметр, t - толщина кольца. Рис. 4.11 Моменты инерции сечений сложной формы Момент инерции сечения сложной формы относительно некоторой оси равен сумме моментов инерций его составных частей относительно той же оси: , (13) что непосредственно следует из свойств определенного интеграла. Таким образом, для вычисления момента инерции сложной фигуры надо разбить ее на ряд простых фигур, вычислить моменты инерции этих фигур, а затем просуммировать их. Пример 3. Определить момент инерции сечения, показанного на рис. 4.12, относительно оси симметрии, a=10 см. 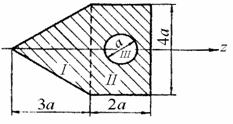 Рис.4.12 Решение. Разбиваем заданное сечение на простейшие элементы: I - Равнобедренный треугольник, II - прямоугольник, III - круг. Момент инерции сложной фигуры относительно оси z согласно формуле (13):  .Определяем моменты инерции слагаемых простейших элементов: Для равнобедренного треугольника:  ; для прямоугольника согласно формуле:  ; для круга согласно формуле:  .Окончательно получим: Iz=4,0a4+10,67a4-0,0491a4=14,6a4=14,6×104=1,46×105 см4. Пример 4. Определить момент инерции симметричного сечения, показанного на рис. 4.13, относительно вертикальной оси симметрии y. Двутавр №10 (ГОСТ 8239-56). Швеллер №5 (ГОСТ 8240-56). 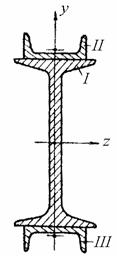 Рис.4.13 Решение. Разбиваем исходное сечение на простейшие элементы, моменты инерций которых приводятся в справочниках: I - двутавр, II и III - швеллеры. По сортаменту на стандартные прокатные профили имеем: Для двутавра №10 (ГОСТ 8239-56): H=10 см, B=7 см, F=14,2 см2, Ix=244 см4, Iy=35,3 см4. Для швеллера №5 (ГОСТ 8240-56): h=5 см, b=3,7 см, F=6,90 см2, Ix=26,1 см4, Iy=8,41 см4, x0=1,35 см. Момент инерции сечения относительно оси y согласно (13)  т.к. оба швеллера расположены идентично относительно оси y. Для двутавра  .Для швеллера  сортам.=26,1 см4.Окончательно имеем:  .Изменение моментов инерции сечения при повороте осей координат Найдем зависимость между моментами инерции относительно осей х, у и моментами инерции относительно осей х1, у1, повернутых на угол 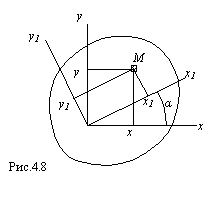 . Пусть Jx> Jy и положительный угол отсчитывается от оси х против часовой стрелки. Пусть координаты точки М до поворота – x,y, после поворота – x1, y1 (рис. 4.14). Рис.4.14 Из рисунка следует: Теперь определим моменты инерции относительно осей х1 и у1: 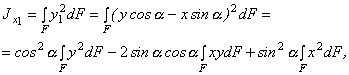 или  . (14)Аналогично:  . (15) (16)Сложив почленно уравнения (14), (15), получим:  ,т.е. сумма моментов инерции относительно любых взаимно перпендикулярных осей остается постоянной и не изменяется при повороте системы координат. Пример 5. Найти моменты инерции прямоугольника (рис.4.15) относительно осей 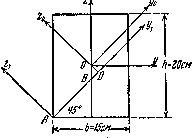 и  и центробежный момент его относительно тех же осей. Рис.4.15 Решение. Центральные оси у и z как оси симметрии будут главными осями; моменты инерции сечения относительно этих осей равны: Центральные моменты относительно повернутых осей  и  равны: Центробежный момент инерции относительно осей и равен: Координаты центра тяжести прямоугольника относительно осей 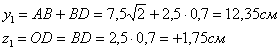и равны: Моменты инерции относительно осей 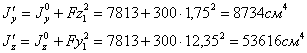и равны: Центробежный момент инерции равен:  Главные оси инерции и главные моменты инерции С изменением угла поворота осей каждая из величин  и  меняется, а сумма их остается неизменной. Следовательно, существует такое значение  , при котором моменты инерции достигают экстремальных значений, т.е. один из моментов инерции достигает своего максимального значения, в то время другой момент инерции принимает минимальное значение. Для нахождения значения  возьмем первую производную от (или ) и приравняем ее нулю: ,или , откуда . (17) Покажем, что относительно полученных осей центробежный момент инерции равен нулю. Для этого приравняем правую часть уравнения (16) нулю: , откуда , т.е. получили ту же формулу для .Оси, относительно которых центробежный момент инерции равен нулю, а осевые моменты инерции принимают экстремальные значения называются главными осями. Если эти оси являются также и центральными, то они называются главными центральными осями. Осевые моменты инерции относительно главных осей называются главными моментами инерции. Обозначим главные оси через  и  . Тогда ,  , . Если сечение имеет ось симметрии, то эта ось всегда является одной из главных центральных осей инерции сечения. В литературе главные оси иногда обозначаются через  и  .Главные моменты инерции  и  могут быть также определены по формулам:  При повороте осей координат удовлетворяется следующее равенство:  Моменты сопротивления относительно главных центральных осей uи vмогут быть подсчитаны по формулам:   где  ,  - координаты точек сечения, наиболее удаленных от главных центральных осей uи v. Эти координаты можно вычислить, используя связь между координатами в повернутых на угол  осях по формулам:  Понятие о радиусе и эллипсе инерции сечения Радиусом инерции плоской фигуры относительно какой-либо оси, называется длина перпендикуляра, отсчитываемая от этой оси и вычисляемая по формуле:   (18)   После определения моментов инерции относительно главных осей можно построить эллипс инерции – это эллипс, полуоси которого равны радиусам инерции относительно главных осей. Радиус инерции  откладывается вдоль главной оси  , а  – вдоль оси  (рис. 4.16). Построение эллипса инерции удобно использовать для анализа правильности определения моментов инерции. Эллипс инерции должен быть вытянут в том направлении, в котором вытянута фигура. Рис.4.16 |