5 Геометрические характеристики. Лекция Геометрические характеристики плоских сечений

• Название: Лекция Геометрические характеристики плоских сечений
• Дата: 02.05.2023
• Размер: 315.73 Kb.
• Имя файла: 5 Геометрические характеристики.docx
• Тип: Лекция; #1102309
• страница: 1 из 4

Лекция 4. Геометрические характеристики плоских сечений
В расчетах конструкций на механическую надежность очень часто приходится оперировать такими характеристиками плоских фигур, как статический момент, осевой и полярный моменты инерции. Хотя вычисление вышеназванных геометрических характеристик относится к числу простейших задач интегрального исчисления, тем не менее, в силу их узкого прикладного значения они практически не рассматриваются во втузовском курсе высшей математики. По установившейся традиции геометрические характеристики плоских фигур изучаются в курсе сопротивления материалов.

Геометрические характеристики – числовые величины (параметры), определяющие размеры, форму, расположение поперечного сечения однородного по упругим свойствам деформируемого элемента конструкции (и, как следствие, характеризующие сопротивление элемента различным видам деформации).
Площадь плоских сечений

Площадь сечения является одной из геометрических характеристик, используемых, главным образом, в расчетах на растяжение и сжатие. При расчетах на кручение, изгиб, а также на устойчивость используются более сложные геометрические характеристики: статические моменты, моменты инерции, моменты сопротивления и т.д.

Проектирование конструкций с оптимальными формами и размерами сечений является одним из путей снижения веса и стоимости машин и сооружений.

Площадь, ограниченная произвольной кривой, есть

(1)

Для вычисления геометрических характеристик сложных сечений, состоящих из простейших фигур, они разбиваются на конечное число n простейших частей. В этом случае

. (2)

Площадь является простейшей геометрической характеристикой сечения, имеет размерность L². Отметим два важных свойства: площадь всегда положительна и не зависит от выбора системы координат.

Для сечений, составленных из профилей стандартного проката, площадь каждого профиля и остальные необходимые для расчетов размеры принимаются по таблицам ГОСТов на прокатную сталь.


При расчетах на изгиб, кручение, сложное сопротивление и устойчивость используются более сложные геометрические характеристики: статические моменты, моменты инерции сечений, которые зависят не только от формы и размеров сечений, но также от положения осей и точек (полюсов), относительно которых они вычисляются.
Статические моменты сечения

Статическим моментом плоского сечения относительно некоторой оси называется, взятая по всей его площади А, сумма произведений площадей элементарных площадок dA на их расстояния от этой оси (рис. 4.1):


; (3)

(4)

(5)

где y_c– расстояние от центра тяжести всего плоского сечения до оси x; x_c – расстояние от центра тяжести всего сечения до оси y.

Статический момент сложного сечения относительно некоторой оси равен сумме статических моментов всех частей этого сечения относительно той же оси:



(6)

В формулах (6) введены обозначения: А₁, А₂, …, А_n – площади простых элементов, составляющих плоское сложное сечение; x₁, y₁, x₂, y₂, x₃,y₃, … , x_n, y_n – координаты центров тяжести простых составляющих сложного плоского сечения относительно выбранных осей х и у.

Из выражений (4) можно определить координаты центра тяжести плоского сечения:

(7)

Для сложного поперечного сечения формулы (7) можно представить в следующем виде

(8)

Зависимости между статическими моментами одного и того же сечения относительно двух параллельных друг другу осей х и х₁, а также у и у₁ имеют вид:

(9)

где параметры a, b показаны на рис. 4.2.



Рис.4.2
У к а з а н и я.

1. Изменение положительного направления оси у вызывает изменение знака статического момента S_x. Аналогично, изменение положительного направления оси х вызывает изменение знака статического момента S_y.

2. Статический момент сечения равен нулю относительно любой оси, проходящей через центр тяжести этого сечения.

3. Если плоское сечение имеет ось симметрии, то эта ось всегда проходит через центр тяжести плоского сечения, а поэтому, согласно п.2, статический момент сечения относительно оси симметрии всегда равен нулю.

4. Если плоское сечение имеет две оси симметрии, то центр тяжести сечения лежит на пересечении этих осей симметрии.
Пример 1.

Определить статический момент полукруга радиусом R (рис. 4.3) относительно горизонтальной оси z, совпадающей с диаметром, и координату центра тяжести y_c.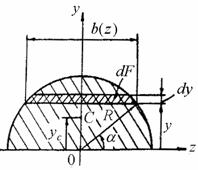



Рис.4.3
Решение.

По формуле (3) имеем . Выделим на рис. 4.3 на расстоянии y элементарную площадку dF с помощью двух хорд, параллельных оси z, на расстоянии dy друг от друга. Как следует из рис. 4.3



тогда

и



Подставляя найденные значения yи dF в выражение S_z, получим





Координата центра тяжести сечения y_c определяется по формуле (7):


Пример 2.

Определить положение центра тяжести неравнобокого уголка 160´100´10 (пренебрегая закруглениями его полок) относительно осей zи y, совпадающих с наружными сторонами контура (рис. 4.4). Найденные значения координат сравнить с табличными значениями по ГОСТ 8510-57.



Рис.4.4
Решение.

Пренебрегая загружением полок уголка, разбиваем фигуру на два прямоугольника, как показано на рис. 4.4. Для первого (1) прямоугольника







Для второго (2) прямоугольника







Координаты центра тяжести сечения определяем по формулам (8):





По данным сортамента с учетом закруглений координаты центра тяжести равны z_c=2,28см;y_c=5,23см.

Для проверки правильности вычислений определим статические моменты относительно центральных осей, которые должны быть равны нулю:



.

Графическая проверка: точка С должна находиться на отрезке С₁С₂.
Моменты инерции плоских сечений простой формы

В дополнение к статическим мо­ментам в системе координат x0y рассмотрим три интегральных выражения:

(10)

Первые два интегральных выраже­ния называются осевыми моментами инерции относительно осей x и y, а третье - центробежным моментом инерции сечения относительно осей x, y.

Для сечений, состоящих из n-числа областей (рис. 4.5), фор­мулы (10) будут иметь вид:





Рис. 4.5
Рассмотрим, как изменяются моменты инерции сечения при параллельном переносе координатных осей x и y (см. рис. 4.6). Преобразуя формулы (10), получим:

(11)



Рис. 4.6
Если предположить, что оси x₁ и y₁ (см. рис. 4.6) являются цен­тральными, тогда и выражения (11) упрощаются и принимают вид:

(12)

Оси называются центральными, если они проходят через центр тяжести фигуры, т. е. статические моменты относительно этих осей равны нулю. Главными осями инерции фигуры называются оси относительно которых центробежный момент инерции равен нулю. Если фигура имеет хотя бы одну ось симметрии, то эта ось является главной осью.

Определим осевые моменты инерции прямоугольника относительно осей x и y , проходящих через его центр тяжести (рис. 4.6). В качестве элементарной пло­щадки dА возьмем полоску шириной b и высотой dy (рис. 4.4). Тогда будем иметь:



Аналогичным образом можно установить, что .

Центробежный момент инерции сечения относительно осей, хотя бы одна из которых является осью симметрии, равен нулю.

Для систем, рассматриваемых в полярной системе координат (рис. 4.7, а), вводится также полярный момент инерции:

.

где - радиус-вектор точки тела в заданной полярной системе ко­ординат.


Рис. 4.7
Вычислим полярный момент инерции круга радиуса R. На рис. 4.7, a показана элементарная площадка, очерченная двумя ра­диусами и двумя концентрическими поверхностями, площадью

.

Интегрирование по площади заменим двойным интегрировани­ем:

.

Hайдем зависимость между полярным и осевыми моментами инерции для круга. Из геометрии видно (рис. 4.7, б), что

,

следовательно,

.

Так как оси x и y для круга равнозначны, то .

Полярный момент инерции кольца может быть найден как разность моментов инерции двух кругов: наружного (радиусом R) и внутреннего (радиусом r):

.

Размерность моментов инерции L⁴. Осевые и полярные моменты инерции всегда положительны, центробежный момент инерции может быть положительным, отрицательным, равным нулю.

Для фигур, имеющих более двух осей симметрии, осевые моменты инерции относительно всех центральных осей равны между собой. К таким фигурам относятся равносторонний треугольник, квадрат, круг и т.д.
Моменты инерции простых сечений

Вычислим моменты инерции простейших фигур.

Прямоугольник

Определим моменты инерции относительно осей, совпадающих со сторонами, и относительно центральных осей.

По определению .



Рис. 4.8
Элемент площади равен dA = bdy,

следовательно .

По формуле , откуда, учитывая что А = bh, y_c = 0,5h, находим

.

Аналогично получим и .
Треугольник

Момент инерции относительно оси х, cовпадающей с основанием,

.

Но dA = b(y)dy, b(y) = (b/h)(h-y).

Cледовательно,

.