5 Геометрические характеристики. Лекция Геометрические характеристики плоских сечений
 Скачать 315.73 Kb.
|
|
Пример 6. Определить радиусы инерции для сечения неравнобедренного уголка 160´100´10 (рис. 4.17). Построить эллипс инерции этого сечения. 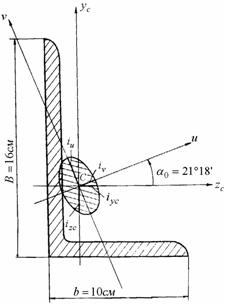 Рис.4.17 Решение. Осевые радиусы инерций сечения определяются по формулам:  Fуголка №16/10 =25,3 см2    Построенный эллипс инерции показан на рис. 4.17. Моменты сопротивления Осевой момент сопротивления относительно рассматриваемой оси – величина равная моменту инерции относительно той же оси отнесенному к расстоянию до наиболее удаленной от этой оси точки  ;  . Полярный момент сопротивления  Осевой и полярный моменты инерции имеют размерность м3. Стандартные прокатные профили В балках из металла обычно применяются сложные поперечные сечения, потому что в них материал может быть использован экономичнее, чем в таких сечениях, как прямоугольник и круг. Так, известно, что валы делают полыми, чтобы удалить ту часть материала, которая слабо работает. Известно также, что при изгибе балок материал около нейтральной оси принимает на себя малые нормальные напряжения и также не может быть использован полностью. Поэтому целесообразнее переделать прямоугольное сечение так, чтобы удалить материал у нейтральной оси и часть его сэкономить, а часть перенести в верхнюю и нижнюю зоны балки, где он будет работать более интенсивно. Так получается из прямоугольного сечения профиль двутавра, обладающего той же прочностью и меньшим весом. Применение двутавра целесообразно при материалах, одинаково сопротивляющихся растяжению и сжатию (большинство металлов). Сечения в виде тавра, применяются или в случаях, вызываемых специальными конструктивными обстоятельствами, или для таких материалов, как чугун, бетон, у которых сопротивления растяжению и сжатию резко разнятся между собой; последнее обстоятельство требует, чтобы напряжения в крайних волокнах были различными. Как видно из изложенного, при решении вопроса о наиболее экономичном проектировании сечения следует стремиться к тому, чтобы при одной и той же площади F получить наибольший момент сопротивления и момент инерции. Это ведет к размещению большей части материала подальше от нейтральной оси. Однако для некоторых сечений можно увеличить момент сопротивления не добавлением, а, наоборот, путем срезки некоторой части сечения, наиболее удаленной от нейтральной оси. Так, например, для круглого сечения срезка заштрихованных сегментов (рис.4.18) несколько увеличивает момент сопротивления, так как при этом мы уменьшаем момент инерции сечения в меньшей степени, чем расстояние до крайнего волокна  . Рис.4.18 Нашей промышленностью выпускаются стандартные прокатные профили (двутавр, швеллер, уголок равнобокий, уголок неравнобокий), которые могут быть использованы как готовые элементы конструкций (балки, стойки, элементы ферм и т.д.). Размеры прокатных профилей стандартизированы и сведены в таблицы сортаментов прокатной стали, которые приводятся в приложениях почти всех учебников и сборников задач по сопротивлению материалов. В этих таблицах приводятся все размеры сечений и основные геометрические характеристики прокатных профилей в соответствии с их номером. Алгоритм расчета геометрических характеристик плоских сечений При анализе геометрических характеристик плоских сечений любой сложности важнейшей задачей является определение положения главных центральных осей, величин главных центральных моментов инерции и моментов сопротивления сечений. Можно рекомендовать следующий порядок определения положения главных центральных осей, величин главных центральных моментов инерции и моментов сопротивления сложного профиля, состоящего из простых частей, характеристики которых либо известны, либо легко определяются. 1. Заданное сечение вычерчивается в определенном масштабе и разбивается на элементы геометрические характеристики которых представлены в сортаменте, либо могут быть вычислены по элементарным формулам, элементы нумеруются, номера элементов указываются на чертеже. 2. Проводим прямоугольную систему осей z, y. Начальные оси могут задаваться произвольно. Однако, для упрощения вычислений удобно, если начальные оси проходят через центр тяжести одного или нескольких элементов сечения, на которые разбито заданное сечение. Все начальные размеры, необходимые для вычисления геометрических характеристик элементов и определения координат центров тяжестей элементов указываются на чертеже. Для прокатных профилей на чертеже сечения указываются необходимые для расчета размеры, взятые из таблиц проката. 3. Определяемкоординаты центров тяжести элементов сечения относительно начальных осей zc, yc. и геометрические характеристики сечений относительно собственных осей элементов Аi,  ,  ,  . Собственные оси элементов – оси, параллельные начальным осям zc, yc. проходящие через центры тяжестей элементов сечения. Замечание.Необходимо проявлять внимательность при определении координат центров тяжестей элементов сечения и их геометрических характеристик, так как ошибки, допущенные на этом этапе не имеют алгоритма проверки и приводят к ошибочным результатам при дальнейших вычислениях. 4. Определяем координаты центра тяжести всего сечения по формулам:  ;  . Центральные оси х, у (оси проходящие через центр тяжести всего сечения), параллельные начальным осям показываются на чертеже. Для самостоятельной проверки правильности, определения координат центра тяжести сложного сечения делается проверка, согласно которой вычисляются статические моменты всего сечения относительно осей  ,  . Должны иметь место равенства  и  в пределах точности производимых вычислений.5. Проводим систему центральных осей , , таким образом, чтобы наиболее просто можно было вычислить моменты инерции частей фигуры относительно этих осей. Для этого определяем моменты инерции частей фигуры относительно собственных центральных осей, проведенных параллельно осям , , используя при этом формулы перехода к параллельным осям (12). Суммируя, получаем значения  ,  ,  .6. Определяем координаты центров тяжести элементов сечения относительно центральных осей сечения:  ;  . Замечание. Геометрические характеристики сечений, координаты центров тяжести сечений относительно начальных и центральных осей целесообразно оформить в виде таблицы (см. пример расчета), 7. Проводим контроль правильности определения координат центров тяжести сечения и его элементов. Для этого вычисляется статический момент сечения относительно центральных осей, которые при правильном расчете должны равняться нулю:  ;  . Замечание. Все расчеты проводятся с ограниченной точностью. Инженерные расчеты, обычно, проводят с учетом 3 – 4 значащих цифр. Оставлять большее число значащих цифр нецелесообразно, так как исходные данные (исходные размеры и значения геометрических характеристик) не обеспечивают большую точность и поэтому результаты с большим числом значащих цифр нельзя считать более достоверными. Точность результата оценивают, обычно, относя невязку (разность между приближенным и точным значением) к точному или приближенному значению. Однако, если результатом вычислений должен быть ноль, такой подход невозможен. В этом случае отдельно подсчитывают положительные  и отрицательные  слагаемые и абсолютное значение невязки и относят невязку к сумме положительных (или отрицательных) слагаемых: . Погрешность инженерных расчетов обычно не должна превышать 3%. 8. Определяем геометрические характеристики сечения – осевые, полярный и центробежный моменты инерции сечения относительно центральных осей  ; ;  ; . Заметим, что площадь, осевые и полярный моменты инерции являются строго положительными характеристиками сечений. Однако, для сечений с отверстиями бывает удобным считать отверстия элементами сечений с отрицательными характеристиками. 9. Определяем положение главных центральных осей. Положительный угол  откладывается против хода часовой стрелки, отрицательный - по ходу часовой стрелки.10. Определяем значения главных центральных моментов инерции  и  , причем ось, относительно которой имеет место максимальный, главный центральный момент инерции, обозначаем буквой u (Imax=Iu), а ей перпендикулярную ось, относительно которой имеет место минимальный, главный центральный момент инерции, обозначаем буквой v(Imin=Iv).Для самостоятельного контроля правильности решения задачи на данном этапе делаются следующие проверки: а) Определяется центробежный момент инерции относительно главных центральных осей  , который согласно определению должен быть равен нулю, Iuv=0.б) Также могут быть определены главные центральные моменты инерции сложного сечения Iu, Iv. в) Должно удовлетворяться равенство:  .11. Для определения моментов сопротивления сложного сечения необходимо определить точки, наиболее удаленные от главных центральных осей, координаты которых относительно главных центральных осей umax и vmax могут быть определены по формулам перехода к повернутым осям. Для проверки, координаты точек, наиболее удаленных от главных центральных осей, могут быть определены и графически непосредственно с чертежа, выполненного в масштабе. 12. Для определения радиусов инерции производятся вычисления по формулам (18). При построении эллипса инерции от центра тяжести сечения по осям uи v откладываем в масштабе чертежа величины iv и iu каждый соответственно перпендикулярно своей оси. На этих отрезках, как на полуосях, строится эллипс инерции. Для проверки (или более точного построения эллипса инерции) могут быть отложены величины  и  .Вопросы для самопроверки - Для чего необходимы геометрические характеристики плоских сечений? - Что такое полярный момент инерции? - Когда используют полярный момент сопротивления? - Для определения каких напряжений используют осевой момент сопротивления? - Что такое главные центральные оси инерции? - Какая геометрическая характеристика используется при определении прогиба? - Какая геометрическая характеристика используется при определении угла закручивания? - Какая геометрическая характеристика используется для определения максимальных касательных напряжений при кручении и максимальных нормальных напряжений при изгибе? - Назовите основные геометрические характеристики поперечных сечений. - Как определяется положение центра тяжести сечения ? - Какие оси называются центральными осями ? - Напишите зависимости между моментами инерции относительно параллельных осей. - Как изменяются моменты инерции при повороте координатных осей? - Какие оси и какие моменты инерции называются главными ? - Напишите значения моментов инерции для простых сечений: прямоугольника, треугольника, круга, полукруга. - В какой последовательности определяется положение главных центральных осей для составных сечений ? - Вставьте (устно) пропущенное слово: Статическим моментом площади сложного сечения называется сумма произведений площадей на расстояние от … до их центров тяжести. - Зависит ли статический момент сечения от расстояния фигуры до оси, относительно которой он вычисляется? - Чему равен статический момент сечения относительно оси yc, проходящей через центр тяжести сечения? 1.  2.  3. |