волс++3. Лекция Классификация и конструкция волоконнооптических кабелей

• Название: Лекция Классификация и конструкция волоконнооптических кабелей
• Дата: 23.01.2023
• Размер: 482.7 Kb.
• Имя файла: волс++3.docx
• Тип: Лекция; #901000
• страница: 2 из 5

Теорема Умова-Пойнтинга

Теорема Умова-Пойнтинга характеризует баланс энергии электромагнитного поля. Запас электромагнитной энергии в объеме V составляет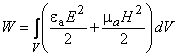

                                                    (4.10)

где   – энергия электрического поля в единице объема;

 – энергия магнитного поля в единице объема.

Используя уравнение Максвелла, получаем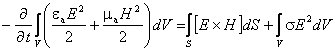

                                 (4.11)

где dS – элемент поверхности S, ограничивающий объемV.

Данное выражение носит название теоремы Умова-Пойнтинга. Левая часть выражения характеризует расход электромагнитной энергии за единицу времени, правая часть показывает, на что расходуется за единицу времени заключенная в объеме энергия.

Первый член правой части выражения (4.11) представляет собой поток энергии, за единицу времени через замкнутую поверхность объема V в окружающее пространство или в объем V от внешних источников.

Количество энергии, распространяющейся в единицу времени через единичную площадку, перпендикулярную направлению потока энергии, выражается векторной величиной

,

называемой вектором Умова-Пойнтинга (вектором Пойнтинга).

Второй член в соответствии с законом Джоуля-Ленца характеризует энергию внутри объема V, преобразованную в тепло за единицу времени.

Направление движения электромагнитной энергии в пространстве показывает направление вектора Пойнтинга. Теорема Пойнтинга позволяет установить связь между напряженностями полей Е и Н на поверхности какого-либо объема с потоком энергии, входящей в этот объем либо выходящей из него.

Уравнения Максвелла дают  возможность точно решить практически любую электродинами­ческую задачу, включая передачу сигналов связи по различным направляющим системам в разных диапазонах частот.

Лекция 5. Расчет параметров передачи двухпроводных направляющих систем

 

Цель лекции: дать основные понятия первичных и вторичных характеристик кабеля.

 

Количественно потери в проводниках можно определить нахождением составляющей вектора Пойнтинга, проникающей в толщу проводников через их поверхность:

                                      .                                          (5.1)

Для единицы длины цилиндрического проводника при синусоидальном изменении поля радиальная составляющая вектора Пойнтинга составляет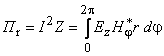

                                         .                                         (5.2)

Полное внутреннее сопротивление проводника Z, представляющее собой сумму активной (R) и реактивной (jωL_внутр) составляющих, определяется выражением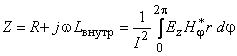

                                                                   (5.3)

где R – активное сопротивление проводника;

L_внутр – внутренняя индуктивность (jωL_внутр – реактивное сопротивление индуктивности);

E_z – продольная составляющая вектора E на поверхности проводника;

Н*_–комплексно–сопряженная величина тангенциальной составляющей вектора Н на поверхности проводника;

r – радиус проводника.  

                      

Следовательно, величины R и L могут быть определены из уравнения (5.2), если известны Е_z и Н_. Величины Е_z и Н_ находят путем решения уравнений Максвелла (4.8) и (4.9) для конкретной направляющей системы.

Полное сопротивление проводника определяется путем решения уравнений Максвелла и проведения соответствующих преобразований: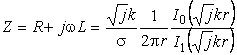

 

                                                                   (5.4)

где R иL – соответственно активное сопротивление и индуктивность проводника;

I₀  – видоизмененная функция Бесселя нулевого порядка первого рода;

I₁  – функция Бесселя первого порядка первого рода.

 

Обычно пользуются заранее рассчитанными таблицами [9], где бесселевы функции и их соотношения сведены в таблицу в виде соответствующих коэффициентов F(kr), G(kr), H(kr), Q(kr).

В симметричном кабеле проводники расположены в непосред­ственной близости друг к другу, поэтому при расчете приходится считаться с эффектом близости.

Таким образом, активное сопротивление симметричных кабелей (СК) состоит из сопротивления постоянному току (R₀), сопротивления за счет поверхностного эффекта (R_П), сопротивления за счет эффекта близости (R_Б) и сопротивления потерь в окружающих металлических массах (R_М) (соседние проводники, экран, оболочка, броня):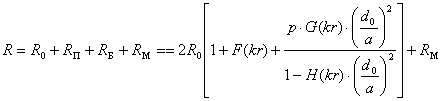

 

     (5.5)

 

где R₀ – сопротивление цепи постоянному току, Ом/км: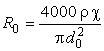

 

                                                                                                (5.6)

 

ρ=1/σ – удельное сопротивление материала жил, Ом·мм²/м;

d₀ – диаметр жил, мм;

R_П,R_Б,R_М – дополнительное сопротивление, соответственно за счет поверхностного эффекта, эффекта близости и потерь в окружающих металлических массах;

χ – коэффициент укрутки, учитывающий увеличение длины цепи за счет скрутки, принимается равным 1,02…1,07;

р – коэффициент, учитывающий потери на вихревые токи в жилах второй цепи элементарной группы, для звездной скрутки р=5; для парной скрутки р=1;

а – расстояние между центрами жил цепи, мм.

 

При звездной скрутке  , при парной скруткеа=d₁, где диаметр изолированной жилы, мм, для кордельной изоляции определяется по формуле:



где d₀ – диаметр токопроводящей жилы, мм;

d_к – диаметр корделя, мм, обычно принимаем 0,6…0,8 диаметра жилы;

Δ – общая толщина лент, наложенных поверх корделя, мм,

 

Δ=n∙t_л,

      n – число лент;

      t_л – толщина ленты.

диаметр изолированной жилы со сплошной или пористой изоляцией определяется:

                                             

где ∆ – радиальная толщина изоляционного слоя, мм;

r₀ – радиус токоподводящей жилы, мм;

k – коэффициент вихревых токов, 1/мм:

 

                                          ;

μ_а – абсолютная магнитная проницаемость,

μ_а=μ₀·μ,Гн/м;  μ₀=4π·10^-7, Гн/м;

μ – относительная магнитная проницаемость;

Индуктивность симметричной кабельной цепи

 

                                                                  (5.7)

где Q(kr) – коэффициент функции Бесселя, учитывающий явление поверхностного эффекта.

 

Коаксиальные кабели используются для высокочастотных систем передачи, поэтому их параметры рассчитывают для частот выше 60 кГц. В этом случае активное сопротивление (Ом/км) состоит из суммы сопротивлений внутреннего (R_а) и внешнего (R_b) проводников с учетом поверхностного эффекта и эффекта близости: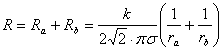

 

                                                                (5.8)

где R_a, R_b– активное сопротивление соответственно внутреннего и внешнего проводников, Ом/км;

r_a, r_b – диаметры соответственно внутреннего и внешнего проводников, мм;

f – частота, Гц.

Для медных проводников формула примет вид: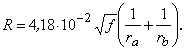

 



Для алюминиевых проводников: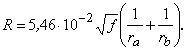

 

 

Индуктивность коаксиальной цепи, Гн/км,состоит из суммы внешней индуктивности между проводами L_внеш и внутренней индуктивности проводников L_A+L_B. Индуктивность медных проводников составляет: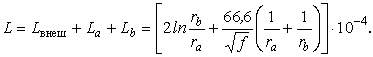

 

                                    (5.9)

 

Для алюминиевых проводников формула примет вид:

                                (5.10)

На рисунке 5.1 представлена частотная зависимость первичных параметров.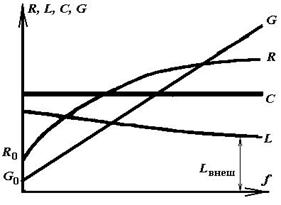



Рисунок 5.1- Частотная зависимость первичных параметров

 

Емкость направляющих систем, Ф/км, может быть рассчита­на как емкость конденсатора (плоский для воздушных линий свя­зи и симметричных кабелей и цилиндрический для коаксиальных кабелей), образованного определенной длины отрезком воздуш­ной линии связи:

 

для симметричного кабеля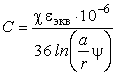

                                                                                 (5.11)

где ε_экв – эквивалентная относительная диэлектрическая прони­цаемость изоляции жил;

ψ – коэффициент, учитывающий близость соседних проводников и металлической оболочки;

 – коэффициент укрутки.

для коаксиального кабеля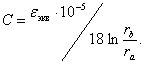

 

                                                                           (5.12)

Проводимость изоляции G, См/км, зависит от проводимости материала изоляции и диэлектрических потерь:

                                        G = G₀+G_пер.                                               (5.13)

Проводимость изоляции, обусловленная диэлектрическими потерями при переменном токе, определяется выражением:

                                         G_пер= ωC·tgδ.                                              (5.14)

 

Вторичные параметры направляющих систем

Вторичными параметрами направляющей системы часто пользуются на практике как наиболее просто поддающими­ся измерению. В свою очередь Z и γ полностью определяются первичными параметрами цепи R, L, C, G.

Волновое сопротивление – это сопротивление, которое встречает электромагнитная волна при распространении вдоль однородной линии без отражения.

                              .                                 (5.15)

 

В диапазоне относительно низких (тональных) частот волновое сопротивление, Ом, составляет

 

                               .                                                  (5.16)

 

 

В диапазоне высоких частот  волновое сопротивление, Ом, равно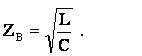

 

                                                                                 (5.17)

 

Коэффициент распространения (1/км) является комплексной величиной и может быть представлен в виде суммы ее действительной и мнимой частей:

                                 .                               (5.18)

 

Действительная часть α и мнимая часть β характеризуют соответственно затухание и изменение фаз тока и напряжения, а также мощности на участке цепи длиной 1 км и называются коэффициентом затухания и коэффициентом фазы.

В диапазоне высоких частот, когда ωL>>R, ωC>>G, формулы для расчета коэффициентов затухания и фазы примут вид: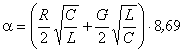

 дБ/км,

                                       рад/км                                       (5.19)

где   характеризует потери в металле, а   – потери в диэлектрике.

Характер частотной зависимости коэффициентов α и β приведен на рисунке 5.2.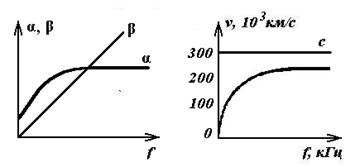



Рисунок 5.2-Частотная зависимость коэффициента затухания, коэффициента фазы и скорости распространения электромагнитной волны

Скорость распространения электромагнитной энергии по цепи связи. Скорость передачи зависит от параметров цепи и частоты тока. Она определяется выражением:

      .                                                 (5.20)

На рисунке 5.2 показана частотная зависимость скорости распространения электромагнитной волны по кабельной линии.

 

Лекция 6. Передача электромагнитной энергии по оптическим кабелям

 

Цель лекции: дать основные сведения О ВОЛС, типах световодов.

 

Волоконно-оптическая линия связи (ВОЛС) – это вид системы передачи, при котором информация передается по оптическим диэлектрическим волноводам, называемым «оптическое волокно».

Волоконно-оптическая сеть – это информационная сеть, связующими элементами между узлами которой  являются волоконно-оптические линии связи. Передача информации по ВОЛС имеет целый ряд достоинств перед передачей по медному кабелю.

Достоинства ВОЛС:

1)     широкая полоса пропускания  обусловлена высокой частотой несущей 10¹⁴ Гц. Это дает потенциальную возможность передачи по одному оптическому волокну потока информации в несколько терабит в секунду;

2)     низкий уровень шумов  в волоконно-оптическом кабеле позволяет увеличить полосу пропускания путем передачи различной модуляции сигналов с малой избыточностью кода;

3)     высокая помехозащищенность объясняется тем, что волокно изготовлено из диэлектрического материала, оно невосприимчиво к электромагнитным помехам со стороны окружающих медных кабельных систем и электрического оборудования. В многоволоконных кабелях также не возникает проблемы перекрестного влияния электромагнитного излучения;

4)     малое затухание светового сигнала в волокне позволяет строить участки линий без ретрансляции протяженностью до   100 километров и более;

5)     малый вес и объем – внешний диаметр оптического кабеля (1,5 см) в несколько раз меньше медного телефонного кабеля с такой же пропускной способностью;

6)     высокая защищенность от несанкционированного доступа обусловлена тем, что ВОК практически не излучает в радиодиапазоне, передаваемую по нему информацию трудно подслушать, не нарушая приемо-передачи. Системы мониторинга (непрерывного контроля) целостности ВОЛС могут мгновенно отключить «взламываемый» канал связи и подать сигнал тревоги;

7)     гальваническая развязка элементов сети – данное преимущество оптического волокна заключается в его изолирующем свойстве. Волокно позволяет избежать электрических «земельных» петель;

8)     взрыво- и пожаробезопасность – из-за отсутствия искрообразования оптическое волокно повышает безопасность сети на химических, нефтеперерабатывающих предприятиях;

9)     экономичность – волокно изготавливают из кварца, более распространенного, в отличие от меди, материала. При этом ВОК позволяет передавать сигналы на значительно большие расстояния без ретрансляции (уменьшается количество повторителей на протяженных линиях);

10)длительный срок эксплуатации – срок службы ВОК составляет 25 лет, за это время может смениться несколько поколений/стандартов приемо-передающей аппаратуры.

Наряду с преимуществами, волоконно-оптические системы имеют ряд недостатков, обусловленных главным образом дороговизной прецизионного монтажного оборудования и надежностью лазерных источников излучения. Высока стоимость интерфейсного оборудования (оптические приемники и передатчики, пассивное коммутационное оборудование, оптические соединители и разветвители). Стоимость работ по монтажу, тестированию и поддержке ВОЛС также остается высокой.

Несмотря на перечисленные недостатки, преимущества от применения ВОЛС значительны, поэтому дальнейшее развитие технологии ВОЛС в информационных сетях является перспективным.