волс++3. Лекция Классификация и конструкция волоконнооптических кабелей
 Скачать 482.7 Kb. Скачать 482.7 Kb.
|
|
Лекция 3. Классификация и конструкция волоконно-оптических кабелей Цель лекции: изучить маркировку и основные элементы волоконно-оптического кабеля. Оптическим кабелем (ОК) называется кабельное соединение, содержащее одно или несколько оптических волокон, объединенных в единую конструкцию, обеспечивающую их работоспособность в заданных условиях эксплуатации [5]. Оптические волокна, модули или жгуты заключают в общую оболочку, поверх которой в зависимости от условий эксплуатации может быть наложен защитный покров. По назначению оптические кабели делятся на магистральные, зоновые, городские, станционные (внутриобъектовые и монтажные). Магистральные ОК предназначены для передачи информации на большие расстояния, и поэтому они должны обладать малым затуханием, дисперсией и большой широкополосностью. Зоновые кабели предназначены для связи областного центра с районами и городами области. Дальность связи, как правило, составляет порядка сотни километров. Городские оптические кабели используются в качестве соединительных линий между районными АТС и узлами связи. Они рассчитаны на короткие расстояния (5...10 км) и большое число каналов. Эти линии, как правило, работают без промежуточных линейных регенераторов. Сельские ОК предназначены для организации сельской телефонной связи, имеют преимущественно четырех волоконную конструкцию и прокладываются в грунт или подвешиваются по опорам. Объектовые кабели служат для передачи различного рода информации внутри объекта. Сюда относятся кабели для информационных систем отдельных объектов (самолет, корабль и др.), а также для организации различных видов учрежденческой связи. Монтажные ОК предназначены для внутри- и межблочного монтажа аппаратуры. По условию прокладки кабели делятся на воздушные, подземные, подводные. Кабели воздушной подвески (см. рисунок 3.1) подвешиваются на опорах различного типа и делятся на: - самонесущие – с несущим тросом или без него, подвешиваемые на опорах ЛЭП и контактной сети железных дорог; - прикрепляемые – крепятся к несущему поводу с помощью диэлектрических шнуров или ленты, или же с помощью специальных зажимов, или спиралевидных отрезков металлической проволоки; - навиваемые – навиваются вокруг существующего, например, фазового провода или провода заземления (грозотроса); - встраиваемые в грозотрос. Кабели подземной прокладки делятся на: - кабели, прокладываемые в кабельной канализации и туннелях; - кабели, закапываемые в грунт; - кабели автоматической прокладки в специальных полиэтиленовых трубах. 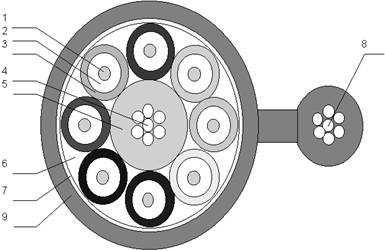 1 – оптическое волокно; 2 – гидрофобный заполнитель; 3 – полимерная трубка; 4 – центральный силовой элемент; 5 – полимерная трубка; 6 – гидрофобный заполнитель; 7 – скрепляющая лента; 8 – синтетическая нить. Рисунок 3.1 - Подвесной оптический кабель Подводные кабели делятся на: - кабели, укладываемые на дно несудоходных рек, неглубоких озер и болот (используются при прохождении водных преград небольшой длины); - кабели, укладываемые на дно морей и океанов (что может означать не только укладку на дно, но и закрепление на определенной глубине, или закапывание в донный грунт на определенную глубину). Основным элементом ОК является оптический волновод – круглый стержень из оптически прозрачного диэлектрика (направляющая среда, структура которой обеспечивает распространение оптического излучения вдоль нее [5]). Оптические волноводы из-за малых размеров поперечного сечения обычно называют волоконными световодами или оптическими волокнами (ОВ). Для изготовления ОВ используют однородные стекла высоких чистоты и качества. При этом в зависимости от назначения кабеля в конструкцию закладываются одномодовые (магистральные), многомодовые градиентные (зоновые и городские) или многомодовые ступенчатые волокна (городские и объектовые кабели). Стеклянное двухслойное волокно для защиты от механических и атмосферных воздействий и усиления конструкции снаружи имеет полимерное покрытие (см. рисунок 3.2). 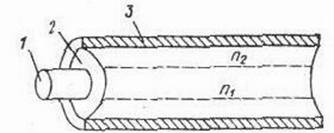 1 – сердцевина; 2 – оболочка; 3 – защитное покрытие. Рисунок 3.2 - Структура оптического волокна В некоторых конструкциях волокно свободно расположено в трубке из фторопласта – оптического модуля (см. рисунок 3.3). Пространство между волокном и модулем иногда заполняется синтетическими нитями. 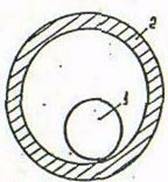 1 – оптоволокно; 2 – трубка. Рисунок 3.3 -Модуль оптический Кроме оптических волокон (модулей), ОК может состоять из следующих элементов: - силовых (упрочняющих) стержней, принимающих на себя продольное усиление; - заполнителей в виде сплошных пластмассовых нитей; - армирующих элементов, повышающих стойкость кабеля к механическим воздействиям; - наружных защитных оболочек, предохраняющих от проникновения влаги и внешних механических воздействий. В зависимости от конструкции сердечника наибольшее распространение получили 3 группы конструкций ОК: кабели повивной скрутки (модульная конструкция), с фигурным (профилированным) сердечником, ленточного типа (плоская конструкция) . Кабели первого типа имеют повивную скрутку сердечника по аналогии с электрическими кабелями (см. рисунок 3.4). 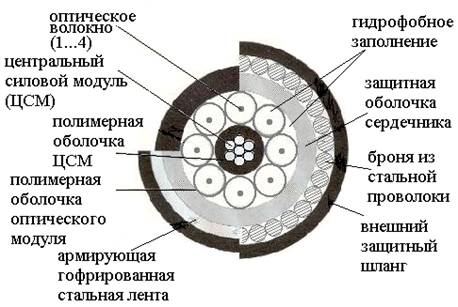 Рисунок 3.4- Модульная конструкция оптического кабеля ОК второй группы (см. рисунок 3.5) имеют в центре армированный силовыми элементами фигурный пластмассовый сердечник с пазами, в которых размещены оптические волокна. Пазы и соответственно волокна расположены по геликоиде, и поэтому волокна не испытывают продольного усиления на разрыв. Такие кабели содержат обычно 4, 6, 8, 10 волокон. Если необходим кабель большей емкости, то в сердечник закладывают несколько таких модулей. 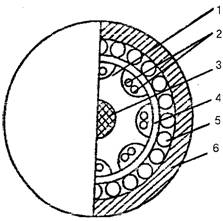 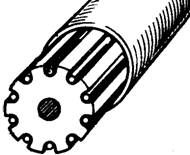 1 – профилированный сердечник; 2 – оптическое волокно; 3 – центральный силовой элемент из стеклопластикового стержня; 4 – внутренняя пластмассовая обмотка; 5 – стеклопластиковые стержни; 6 – наружная полиэтиленовая оболочка. Рисунок 3.5- Магистральный оптический кабель 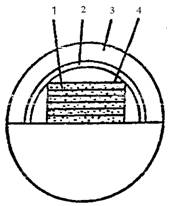 а) 1 – ОВ; 2 – демпфирующая оболочка; 3 – внешняя защитная оболочка; 4 – лентаю.  б) 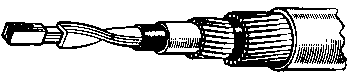 в) а – структура кабеля; б – лента с волокнами; в – вид кабеля сбоку. Рисунок 3.6- Кабель ленточного типа Кабель ленточного типа (см. рисунок 3.6) состоит из набора плоских пластмассовых лент, в которые вмонтировано определенное число (чаще всего 12) оптических волокон. В стопке расположено 6, 8 или 12 лент. Маркировка оптических кабелей Оптические кабели связи (ОКС) выпускаются многими компаниями, как зарубежными (Alcatel, AMP, BICCCablesCompany/BICCKWOKabelGmbH, Focas, Fujikura, Hellukabel, Lucent Technologies, Mohawk/CDT, NC Сables, Philips, Pirelli, Samsung, Siemens, Sumitomo), так и Российскими («Москабельмет», Москва (теперь «Москабель-Фуджикура»); «Оптен», Санкт-Петербург; «Оптика-кабель», Москва (теперь «Москабель-Фуджикура»); «Самарская оптическая кабельная компания (СОКК)», Самара. Российские компании, как правило, используют импортное оборудование и волокно (например, волокна фирмы Corning, Alcatel, Fujikura), их продукция соответствует мировому уровню качества и подтверждена соответствующими сертификатами, что позволяет использовать ее с выгодой для отечественного потребителя [6]. Как показывает практика, разные фирмы-производители используют различные обозначения для оптических кабелей, поэтому маркировка иногда различается.
Лекция 4. Электродинамика направляющих систем Цель лекции: изучить основные уравнения электромагнитного поля,уравнения Максвелла, теорема Умова-Пойнтинга. Основные уравнения электромагнитного поля, называемые уравнениями Максвелла, обобщают два основных закона электротехники: закон полного тока и закон электромагнитной индукции. Согласно закону полного тока линейный интеграл напряженности магнитного поля по любому замкнутому контуру равен полному току, протекающему через поверхность, ограниченную этим контуром. Полный ток складывается из токов смещения и токов проводимости: Уравнение (4.1) называется первым уравнением Максвелла. В соответствии с законом электромагнитной индукции, открытым Фарадеем, электродвижущая сила, возникающая в контуре при изменении магнитного потока Ф, пронизывающего поверхность, ограниченную контуром, равна скорости изменения этого потока со знаком минус: Это уравнение называют вторым уравнением Максвелла. Уравнения (4.1) и (4.2) представлены в интегральной форме. Для решения практических задач чаще используются уравнения Максвелла в дифференциальной форме: rotH = σE + εa (дЕ/дt) = σE + jωεaE, (4.3) rot Е = – μа(дН/дt) = – j ωμаH. (4.4) Здесь σ, εa, μа — соответственно проводимость, абсолютные диэлектрическая и магнитная проницаемости среды; σE – плотность тока проводимости (т.е. тока в металлических массах); jωεaE – плотность тока смещения (т.е. тока в диэлектрике). С физической точки зрения уравнение (4.3) показывает, что изменяющееся электрическое поле создает вокруг себя магнитное поле (вихрь Н), а уравнение (4.4) – что всякое изменение магнитного поля сопровождается появлением электрического поля (вихрь Е). В целом изменение одного поля приводит к появлению другого поля, в результате действует и распространяется комплексное электромагнитное поле, переносящее электромагнитную энергию в пространстве и направляющих системах. Среды могут существенно отличаться друг от друга по величине удельной проводимости σ. Чем больше удельная проводимость, тем больше плотность тока проводимости. Часто для упрощения анализа используются понятия идеального проводника и идеального диэлектрика. Идеальный проводник – это среда с бесконечно большой удельной проводимостью, а идеальный диэлектрик – среда, не обладающая проводимостью. В идеальном проводнике может существовать только ток проводимости Iпр=σE, а в идеальном диэлектрике – только токи смещения Iсм=jωεаE. При рассмотрении процессов в проводниках током смещения можно пренебречь и расчетные формулы приобретут вид: 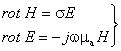 . (4.5) . (4.5)В диэлектрических направляющих системах (диэлектрические волноводы, световоды), а также в атмосфере преобладают токи смещения и для их анализа пользуются уравнениями: 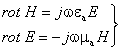 . (4.6) . (4.6)Так как направляющие системы имеют цилиндрическую конструкцию, то наиболее часто записывают уравнения Максвелла в цилиндрической системе координат (оси z, r, φ), при этом ось z совмещают с осью направляющей системы (см. рисунок 4.1). 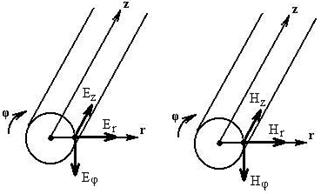 Рисунок 4.1- Компоненты электромагнитного поля в цилиндрической системе координат В цилиндрической системе координат уравнения Максвелла для проводников имеют вид: дEz/дr = j ω μаHφ , . (4.7) (дHφ/дr) + (Hφ/r) – 1/r (дHr/дφ) = σEz После дифференцирования Hr по φ и Hφ по r и подстановки полученных производных в указанные уравнения получим: д2Еz/дr2 + 1 /r (дEz/дr) + 1/r2 (дHr/дφ) = jk2Ez (4.8) где k = Решая данное уравнение, находим Ez, величина Hφ определяется из уравнения Hφ = [1/(jωμа)]·[дEz/дr]. (4.9) Зная компоненты электромагнитного поля E и Н,можно определить энергию, распространяющуюся вдоль проводника, а также энергию, поглощаемую или излучаемую им. | ||||||||||||||||||||||||||||||||||||
