Диск. Лекция 9. Лекция Комбинаторика. Размещения и сочетания
 Скачать 47.28 Kb. Скачать 47.28 Kb.
|
|
Лекция 9. Комбинаторика. Размещения и сочетания Цель: ознакомить студентов с основными комбинаторными формулами. Структура лекции: 1. Упорядоченные и неупорядоченные выборки. 2. Сочетания и размещения. Основная задача комбинаторики - пересчет и перечисление элементов в конечных множествах. Если нас интересует, сколько элементов заданного конечного множества обладает некоторым свойством или набором свойств, то это задача пересчета; если надо выделить все элементы множества, удовлетворяющие заданным свойствам, то это задача перечисления. Наиболее часто применяются в комбинаторике при доказательствах два правила: суммы и произведения. Пусть Х конечное множество, состоящее из n элементов; тогда говорят, что объект х из Х может быть выбран n способами и пишут Х=n. Если Х1, …, Хn – попарно непересекающиеся множества, т.е. Хi 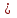 Хj= при i j, то Хj= при i j, то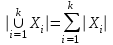 - это правило суммы. - это правило суммы.Для k=2 оно может быть сформулировано так: если объект х может быть выбран m способами, а у - другими n способами, то выбор "либо х, либо у" может быть осуществлен m+n способами (выборы элементов х и у взаимно исключены). Правило произведения формулируется так. Если объект х может быть выбран m способами и после каждого из таких выборов объект у в свою очередь может быть выбран n способами, то выбор упорядоченной пары (х, у) может быть осуществлен mn способами (выборы х, у - независимы). В общем случае, если объект х1 может быть выбран n1 способами, после чего объект х2 может быть выбран n2 способами и для любого 2 i m-1 после выбора объектов х1, х2, …, хi объект хi+1 может быть выбран ni+1 способами, то выбор упорядоченной последовательности из m объектов (х1, х2, …, хm) может быть осуществлен n1 n2 … nm способами. Набор элементов хi1, …, хir из множества Х={х1, …, хn} называется выборкой объема r из n элементов, или (n, r) - выборкой. Выборка называется упорядоченной, если порядок следования элементов в ней задан; если порядок не существенен, то она называется неупорядоченной. В выборках могут допускаться или не допускаться повторения элементов. Упорядоченная (n, r) - выборка, в которой элементы могут повторяться, называется (n, r)-размещением с повторениями; если все элементы упорядоченной (n, r)-выборки попарно различны, то она называется (n, r)-размещением без повторений, или просто (n, r)-размещением. (n, n)-размещения без повторений называются перестановками множества Х. Неупорядоченная (n, r)-выборка, в которой элементы могут повторяться, называется (n, r)-сочетанием с повторениями. Если элементы неупорядоченной (n, r)-выборки попарно различны, то она называется (n, r)-сочетанием без повторений, или просто (n, r)-сочетанием. Заметим, что любое (n, r)-сочетание можно рассматривать как r-элементное подмножество n-элементного множества. Например, пусть Х={1, 2, 3}. 1) (1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3) - (3, 2)-размещения с повторениями; 2) (1, 2), (1, 3), (2, 1), (2, 3), (3, 1), (3, 2) - (3, 2)-размещения без повторений; 3) (1, 2, 3), (1, 3, 2), (3, 2, 1), (2, 1, 3), (3, 1, 2), (2, 3, 1) - перестановки множества Х; 4) {1, 1}, {1, 2}, {1, 3}, {2, 2}, {2, 3}, {3, 3} - (3, 2)-сочетания с повторениями; 5) {1, 2}, {1, 3}, {2, 3} - (3, 2)-сочетания без повторений. Число (n, r)-размещений с повторениями обозначают 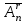 , без повторений , без повторений 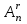 . Число перестановок n-элементного множества обозначается Pn (т.е. Pn = . Число перестановок n-элементного множества обозначается Pn (т.е. Pn =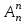 ). Число (n, r)-сочетаний с повторениями обозначается ). Число (n, r)-сочетаний с повторениями обозначается 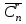 , а без повторений - , а без повторений - 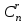 . .Утверждение 1. 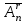 = nr. = nr.Действительно, каждое (n, r)-размещение с повторениями является упорядоченной последовательностью длины r, причем каждый член этой последовательности может быть выбран одним из n способов, отсюда по правилу произведения 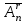 = n n … n = nr. = n n … n = nr.(В частности, это соотношение определяет количество различных чисел, записанных в r позициях, в системе счисления с основанием n). Утверждение 2. 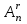 = n (n-1)(n-2) … (n-r+1) = = n (n-1)(n-2) … (n-r+1) = 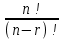 , при r n и , при r n и 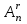 =0, r > n. =0, r > n.Действительно, первый член упорядоченной последовательности из r элементов может быть выбран n способами, второй - (n-1) способом, последний - (n – r + 1) способами. По обобщенному правилу произведения получаем требуемую формулу. Следствие 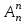 = Pn = n (n - 1) … (n – n + 1) = n! = Pn = n (n - 1) … (n – n + 1) = n!Утверждение 3. 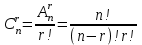 , при r n, , при r n, 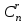 =0 при r>n. =0 при r>n.Действительно, каждое (n, r)-сочетание можно упорядочить r! способами, т.е. 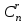 в r! раз меньше, чем в r! раз меньше, чем 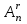 . Из этой формулы видно . Из этой формулы видно 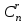 = = 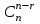 . .Утверждение 4. 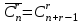 . .Действительно, каждому (n, r)-сочетанию В с повторениями, составленному из элементов множества Х = {x1, …, xn}, поставим в соответствие вектор (В) длины n+r-1 из r нулей и n-1 единиц такой, что число нулей, находящихся между (i-1)-ой и i единицами, где 2 i n-1 будет равно числу элементов xi, входящих в сочетание В, а число нулей, стоящих перед первой единицей (после (n-1)-ой единицы) равно числу элементов x1 (соответственно xn), входящих в В. Например, пусть Х={1, 2, 3, 4}, n=4, пусть r=6, тогда если В={2, 2, 3, 3, 3, 4} - (4, 6)-сочетание с повторением, то (В) = 100100010. С другой стороны, если (В1)=110010000, то В1 = {3, 3, 4, 4, 4, 4}. Это соответствие между (n, r)-сочетаниями с повторениями и векторами, содержащими n-1 единицу и r нулей, взаимно однозначны. Число векторов размерности n+r-1 с n-1 единицами и r нулями равно 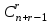 , что и доказывает утверждение. , что и доказывает утверждение.Заметим, что 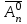 = = 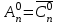 = = 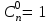 . .Размещения и функциональные отображения. Классической задачей комбинаторики является задача определения числа способов размещения некоторых объектов в каком-то количестве "ящиков" так, чтобы были выполнены заданные ограничения. Формально эта задача формулируется так: Пусть Х = r, Y = n. Обозначим через YХ множество всех отображений f : X Y. Сколько существует функциональных отображений f : X Y, удовлетворяющих заданным ограничениям? Если на эти отображения ограничений нет, то имеет место Утверждение 5. YХ = 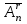 = nr = YX. = nr = YX.Действительно, пусть Х = {x1, …, xr}. Тогда любое отображение f : ХY можно представить в виде упорядоченной последовательности (f(x1), f(x2), …, f(xr)), где f(xi)Y, т.е. мы установили взаимно однозначное соответствие между множеством функциональных отображений и множеством упорядоченных выборок с повторениями объема r из множества Y объема n, а их число равно nr. (Если Х - объекты, а Y- "ящики", то функция f указывает для каждого объекта хХ "ящик" f(x)Y, в котором данный объект находится). Легко найти число размещений, для которых каждый "ящик" содержит не более одного объекта – такое размещение соответствует однозначным функциям (инъективным отображениям). Утверждение 6. Число инъективных отображений f : X Y (т.е. таких, что из f(x1)= f(x2) х1=х2 ) равно 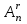 . .Действительно, в этом случае все члены упорядоченной последовательности (f(x1), f(x2), …, f(xr)) должны быть различны, то есть эта последовательность является размещением без повторений. Следствие. Если Sn - множество всех биективных отображений n-элементного множества в себя (т.е. осуществляющих взаимно однозначное отображение элементов множества в себя), то их количество | Sn | равно 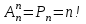 |
