Лекция Методы системной динамики
 Скачать 310.18 Kb. Скачать 310.18 Kb.
|
|
Лекция 5. Методы системной динамики Системная динамика – это метод имитационного моделирования, основанный на представлении системы на высоком уровне абстракции как совокупности потоков, накопителей, вспомогательных переменных и субмоделей со своими элементами. В основе концепции системной динамики лежит представление о функционировании системы как совокупности потоков информации, энергии, финансов, продукции и т.п. Начало развития системной динамики связывают с работами Джея Форрестера и Дэнниса Мидоуса (1950 г.), в которых рассматриваются модели глобального развития человечества. Этапы разработки модели системной динамики 1. Анализ статистических данных. Идентификация причинно-следственных связей. 2. Структуризация объекта. Разработка когнитивной модели в виде когнитивной карты причинно-следственных связей. 3. Построение системной диаграммы объекта, где указываются связи между элементами. 4. Разработка математической модели, представляемой системой динамических уравнений. Расчет коэффициентов модели с использованием методов статистики. 5. Реализация модели. 6. Проведение численных экспериментов. Калибровка модели. Верификация модели на статистических данных (подтверждение адекватности модели). 7. Поиск лучших управленческих решений с помощью модели системной динамики. Приведем «условную» классификацию моделей системной динамики. Модели системной динамики подразделяют на: 1) нелинейные модели, реализуемые в виде системы нелинейных уравнений; линейные модели, представляемые систему линейных уравнений; 2) устойчивые модели, параметры которых при незначительных изменениях внешней среды меняются незначительно; неустойчивые модели, параметры которых чувствительны к воздействиям внешней среды. 3) детерминированные, параметры которых не зависят от случайных факторов; стохастические, на параметры которых оказывают влияние случайные воздействия. Основные преимущества использования системно-динамического подхода в имитационном моделировании - моделирование сценариев – просчет различных вариантов будущего при изменении исходных данных; - выявление наиболее критичных факторов в моделируемой среде; - наглядность вводимых данных и получаемых результатов; возможность представления в виде графа причинно-следственных связей, таблиц и диаграмм; - интерактивность имитационной модели. Возможность управляющих воздействий в любом направлении в любой момент времени. Идентификация причинно-следственных связей Первым шагом разработки модели системной динамики является идентификация причинно-следственных связей, определение полярности и лаговой зависимости между переменными. Для определения причинно-следственных связей и лаговых характеристик можно использовать статистические тесты (например, тест Гренджера), позволяющие проверять гипотезы о причинно-следственной зависимости между показателями. Остановимся на понятиях причинности. Для этого приведем два определения – определение Кейнса и Чена, а также определение Гренджера. Определение Кейнса и Чена. Назовем 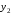 причиной причиной 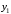 (обозначается: (обозначается: 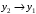 ), если точность предсказания ), если точность предсказания 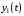 , полученного по наблюдениям , полученного по наблюдениям 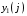 и и 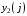 , где , где 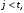 выше, чем по наблюдениям только выше, чем по наблюдениям только 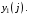 Определение Гренджера. Назовем 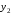 причиной причиной 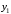 , если , если 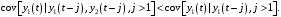 Тест на причинность Гренджера (нобелевская премия 2003 г.) – процедура проверки причинно-следственных связей между временными рядами. Основная идея теста: значения (изменения) временного ряда 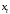 , являющегося причиной изменения временного ряда , являющегося причиной изменения временного ряда 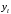 , должны предшествовать изменениям этого временного ряда и вносить значимый вклад в прогноз его значений. , должны предшествовать изменениям этого временного ряда и вносить значимый вклад в прогноз его значений.В тесте проверяются две нулевые гипотезы: «х не является причиной y по Гренджеру», «y не является причиной xпо Гренджеру». Для проверки гипотез строятся две регрессии: 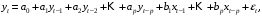 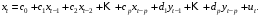 Для каждой регрессии нулевая гипотеза заключается в том, что коэффициенты при лагах второй переменной одновременно равны 0: 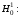 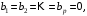 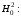 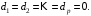 Гипотезы можно проверить с помощью F-теста. Если в результате F-теста: 1) 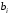 – статистически значимы как группа, а – статистически значимы как группа, а 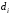 – нет, то направление причинности – нет, то направление причинности 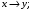 2) 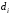 – статистически значимы как группа, а – статистически значимы как группа, а 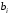 – нет, то направление причинности – нет, то направление причинности 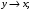 3) обе группы коэффициентов статистически значимы, то можно говорить о двунаправленной зависимостью или зависимостью с обратной связью; 4) обе группы коэффициентов статистически не значимы, то причинная связь отсутствует. После выявления причинно-следственных связей строится диаграмма причинно-следственных связей (когнитивную карту). Когнитивная карта Когнитивная карта ситуации представляет собой ориентированный взвешенный граф, в котором вершины взаимнооднозначно соответствуют базисным факторам ситуации, в терминах которых описываются процессы в ситуации. Множество первоначально отобранных базисных факторов может быть верифицировано с помощью технологии data mining, позволяющей отбросить избыточные факторы, слабо связанные с ядром базисных факторов; определяются непосредственные взаимосвязи между факторами путем рассмотрения причинно-следственных цепочек, описывающих распространение влияний одного фактора на другие факторы. Считается, что факторы, входящие в посылку “если…” цепочки “если…, то…”, влияют на факторы следствия “то…” этой цепочки, причем это влияние может быть либо усиливающим (положительным), либо тормозящим (отрицательным), либо переменного знака в зависимости от возможных дополнительных условий. При этом один элемент оказывает усиливающее влияние на другой 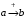 , если увеличение (уменьшение) первого ведет к большему увеличению (уменьшению) второго, чем в случае, когда первый элемент остался бы неизменным. , если увеличение (уменьшение) первого ведет к большему увеличению (уменьшению) второго, чем в случае, когда первый элемент остался бы неизменным.При этом один элемент оказывает уравновешивающее влияние на другой 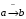 , если увеличение (уменьшение) первого ведет к большему уменьшению (увеличению) второго, чем в случае, когда первый элемент остался бы неизменным. , если увеличение (уменьшение) первого ведет к большему уменьшению (увеличению) второго, чем в случае, когда первый элемент остался бы неизменным.В результате могут быть обозначены контуры обратной связи: - балансирующие (отрицательные) (B); - усиливающие (положительные) (R). Пример усиливающей обратной связи:  +   Количество клиентов Новые клиенты    R  + Пример балансирующей обратной связи:  -   Спрос Цена  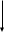   B   + +  Предложение Когнитивная карта отображает лишь факт наличия влияний факторов друг на друга. В ней не отражается ни детальный характер этих влияний, ни динамика изменения влияний в зависимости от изменения ситуации, ни временные изменения самих факторов. Учет всех этих обстоятельств требует перехода на следующий уровень структуризации информации, отображенной в когнитивной карте, т. е. к когнитивной модели. На этом уровне каждая связь между факторами когнитивной карты раскрывается до соответствующего уравнения, которое может содержать как количественные (измеряемые) переменные, так и качественные (не измеряемые) переменные. При этом количественные переменные входят естественным образом в виде их численных значений. Каждой же качественной переменной ставится в соответствие совокупность лингвистических переменных, отображающих различные состояния этой качественной переменной (например, покупательский спрос может быть “слабым”, “умеренным”, “ажиотажным” и т. п.), а каждой лингвистической переменной соответствует определенный числовой эквивалент в шкале [0,1]. По мере накопления знаний о процессах, происходящих в исследуемой ситуации, становится возможным более детально раскрывать характер связей между факторами. Здесь существенную помощь может оказать использование процедур data mining. Формально когнитивная модель ситуации может быть, как и когнитивная карта, представлена графом, однако каждая дуга в этом графе представляет уже некую функциональную зависимость между соответствующими базисными факторами, т. е. когнитивная модель ситуации представляется функциональным графом. Построение когнитивной (графовой) модели проблемной ситуации 1. Выделение факторов, характеризующих проблемную ситуацию: 1.1. Выделение базисных (основных) факторов, описывающих суть проблемы. Выделение в совокупности базисных факторов целевых факторов. Например, суть проблемы неплатежей налогов можно сформулировать в факторах “Неплатежи налогов”, “Доходы бюджета”, “Расходы бюджета”, “Дефицит бюджета” и др. 1.2. Определение факторов, влияющих на целевые факторы. Эти факторы в модели будут являться потенциально возможными рычагами воздействия на ситуацию. Например, при решении проблемы неплатежей налогов это будут факторы “Собираемость налогов”, “Политическая стабильность региона”, “Финансовое состояние региона”, “Инвестиционный рейтинг региона” и др. 1.3. Определение факторов-индикаторов, отражающих и объясняющих развитие процессов в проблемной ситуации и их влияние на различные сферы (экономическую, социальную, политическую и др.). 2. Группировка факторов по блокам. Объединяются в один блок факторы, характеризующие данную сферу проблемы и определяющие процессы в этой сфере. Здесь возможны варианты в зависимости от специфики проблемы, целей анализа, количества субъектов ситуации и т. д. Например, геополитический, макро- и микроэкономический блок, социальные, демографические, отраслевые. федеральные и региональные блоки: 2.1. Выделение в блоке группы интегральных показателей (факторов), по изменению которых можно судить об общих тенденциях в данной сфере. Например, фактор “Дефицит бюджета” обобщенно характеризует ситуацию в бюджетной сфере. 2.2. Выделение в блоке показателей (факторов), характеризующих тенденции и процессы в данной сфере более детально. Например, факторы “Государственные закупки”, “Государственные трансфертные платежи” и др. более конкретно характеризуют ситуацию в бюджетной сфере. 3. Определение связей между факторами: 3.1. Определение связей и взаимосвязей между блоками факторов. Это позволит определить основные направления влияния факторов разных блоков друг на друга. 3.2. Определение непосредственных связей факторов внутри блока: 3.2.1. Определение направления влияний и взаимовлияний между факторами. Например, фактор “Уровень налогового бремени” влияет на “Неплатежи налогов”. 3.2.2. Определение позитивности влияния (положительное, отрицательное, +\-) Например, увеличение (уменьшение) фактора “Уровень налогового бремени” увеличивает (уменьшает) “Неплатежи налогов” – положительное влияние, а увеличение (уменьшение) фактора “Собираемость налогов” уменьшает (увеличивает) “Неплатежи налогов”. 3.2.3. Определение силы влияния и взаимовлияния факторов (слабо, сильно). Например, увеличение (уменьшение) фактора “Уровень налогового бремени” “значительно” увеличивает (уменьшает) “Неплатежи налогов”. 3.3. Определение связей между факторами различных блоков. 4. Проверка адекватности модели, т. е. сопоставление полученных результатов с характеристиками системы, которые при тех же исходных условиях были в прошлом. Если результаты сравнения – неудовлетворительны, то модель корректируется и переходят к п.  Системная диаграмма Структурно модель системной динамики включает следующие элементы: 1) Уровни (накопители) 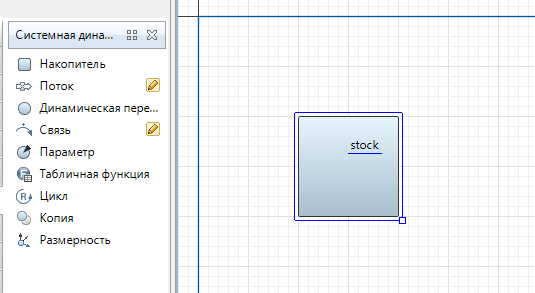 Уровни характеризуют накопленные значения величин внутри системы (заготовки, товары, банковская наличность, уровень оптимизма и т.д.) Уровни представляют собой значения переменных, накопленные в результате разностей между входящими и выходящими потоками. Каждый уровень описывается переменной величиной 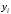 , зависящей от разностей. , зависящей от разностей.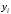   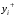 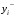  Уравнение уровня: Новый уровень= Текущий уровень+ Входящий поток-Выходящий поток. 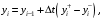 в дифференциальной форме:  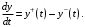 2) Потоковая связь ( ) – дуга потоковой диаграммы, связывает уровни с уровнями, истоками и стоками. Проходит через темп. 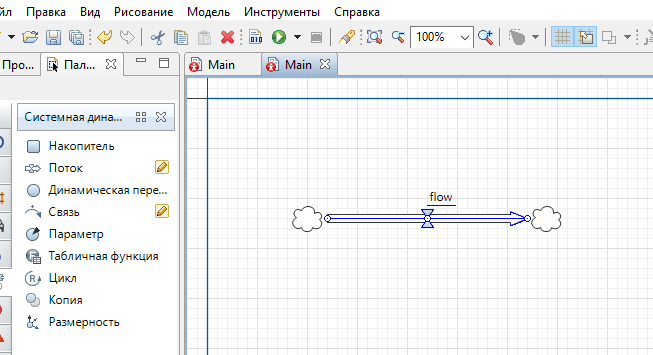  3) Темп ( ) – обозначает скорость потока, проходящего по соответствующей дуге потоковой сети. 3) Темп ( ) – обозначает скорость потока, проходящего по соответствующей дуге потоковой сети.  4) Озеро ( ) – нулевой уровень потоковой сети. 4) Озеро ( ) – нулевой уровень потоковой сети.5)Информационная связь – может соединять параметры, переменные и уровни с темпами, переменными и выходами 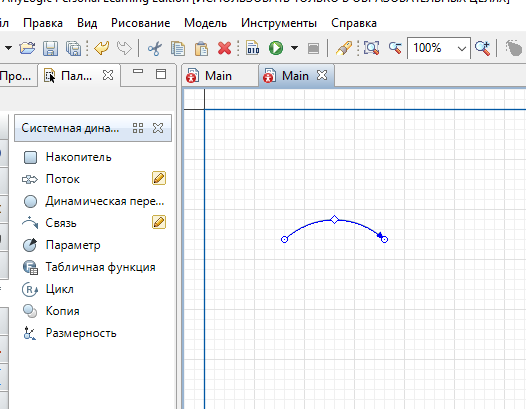 6) Переменная и параметр  Модель развития эпидемии В современном здравоохранении одной из актуальных проблем является профилактика и предотвращение массового распространения инфекционных заболеваний различной природы. Скорость распространения эпидемии зависит от принимаемых в здравоохранении мер (в том числе вакцинации), влияющих на параметры процессов инфицирования и выздоровления. Поэтому исследование процесса развития эпидемии в целях предотвращения массовых заражений, является в настоящий момент социально значимой задачей. В своих исследованиях мы опирались на классическую математическую модель развития эпидемии, описанную в работе [3]. В данной модели исследуется зависимость динамики числа заболевших (например, гриппом) и выздоровевших после болезни. Постановка задачи. Рассмотрим сложную систему – общество, элементами которого являются люди. Выделим следующие группы (подсистемы) людей: ● инфицированные (заболевшие гриппом к определенному моменту времени); ● выздоровевшие (выздоровевшие после болезни гриппом); ● не вакцинированные (восприимчивые к гриппу); ● вакцинированные (невосприимчивые к гриппу). Параметрами процесса развития эпидемии выступают: ● infection_rate (темп заболевания) – доля заболевающих гриппом в единицу времени (от 0 до 1) среди восприимчивых к гриппу людей; ● recovery_rate (темп выздоровления) – доля выздоравливающих в единицу времени (от 0 до 1) среди всех людей, заболевших гриппом. Требуется: провести исследование динамики численности группы инфицированных и группы выздоровевших людей в зависимости от параметров процесса развития эпидемии и начальной численности всех групп населения. Построение модели. Имитационная модель развития эпидемии относится к классу моделей системной динамики. Для наглядного представления такого типа моделей принято строить потоковые диаграммы. Элементами потоковой диаграммы для данного примера являются: 1) Уровни (узлы сети, обозначающие переменные состояния модели): ● susceptible (не вакцинированные) – общее число людей, восприимчивых к гриппу; ● infected (инфицированные) – общее число людей, заболевших гриппом; ● recovered – общее число людей, выздоровевших после болезни. 2) Постоянныепараметры: infection_rate; recovery_rate; 3) Темпы (скорость потока, проходящего по дуге потоковой сети): ● 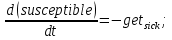 ● 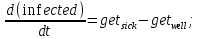 ● 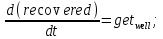 где темпы ● get_sick – число людей, заболевших в единицу времени, get_sick = infected*susceptible*infection_rate; ● get_well – число людей, выздоровевших в единицу времени, get_well = infected*recocery_rate. Потоковая диаграмма модели изображена на рис.11.  Susceptible         Recovered Infected             get_sick get_well    Recovery_rate Infection_rate Потоковая диаграмма развития эпидемии Реализация модели в системе AnyLogic-ple-7.3.6: 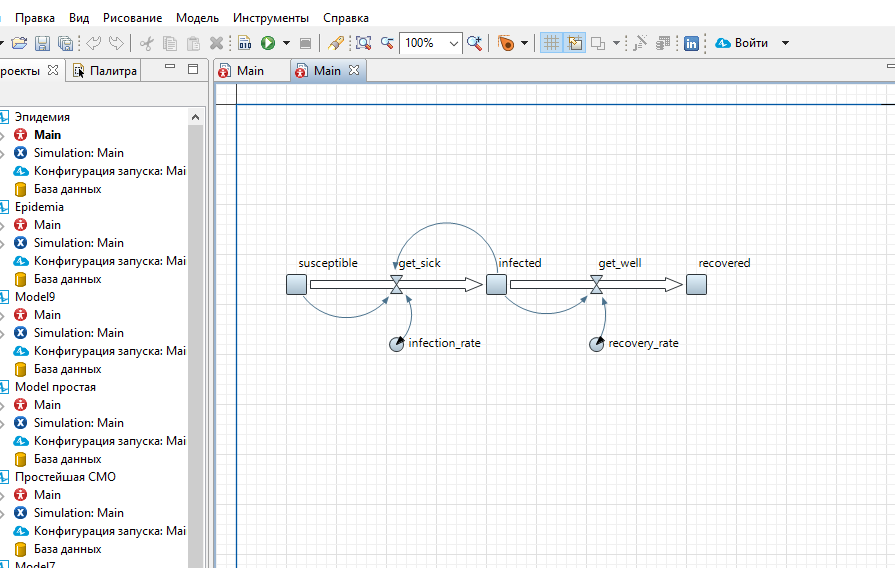 |
