3_Лекции_по_ТОЭ_11-15. Лекция n 11. Особенности составления матричных уравнений при наличии индуктивных связей и ветвей с идеальными источниками
 Скачать 0.74 Mb. Скачать 0.74 Mb.
|
|
Линейные соотношения в линейных электрических цепях При изменении в линейной электрической цепи ЭДС (тока) одного из источников или сопротивления в какой-то ветви токи в любой паре ветвей m и n будут связаны между собой соотношением
где А и В – некоторые в общем случае комплексные константы. Действительно, в соответствии с (1) при изменении ЭДС в k – й ветви для тока в m – й ветви можно записать
и для тока в n – й ветви –
Здесь и - составляющие токов соответственно в m – й и n – й ветвях, обусловленные всеми остальными источниками, кроме . Умножив левую и правую части (10) на , вычтем полученное соотношением из уравнения (9). В результате получим
Обозначив в (11) Отметим, что в соответствии с законом Ома из уравнения (8) вытекает аналогичное соотношение для напряжений в линейной цепи. В 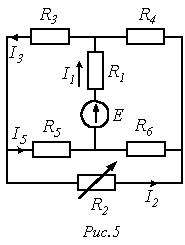 качестве примера найдем аналитическую зависимость между токами и в схеме с переменным резистором на рис. 5, где ; качестве примера найдем аналитическую зависимость между токами и в схеме с переменным резистором на рис. 5, где ; Коэффициенты А и В можно рассчитать, рассмотрев любые два режима работы цепи, соответствующие двум произвольным значениям . Выбрав в качестве этих значений и , для первого случая ( ) запишем 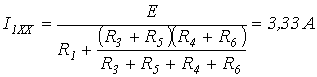 . .Таким образом, При (режим короткого замыкания) 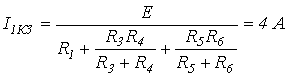 , ,откуда 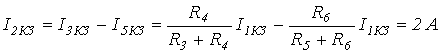 . .На основании (8) 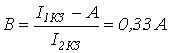 . .Таким образом, Принцип компенсации Принцип компенсации основан на теореме о компенсации, которая гласит: в любой электрической цепи без изменения токов в ее ветвях сопротивление в произвольной ветви можно заменить источником с ЭДС, численно равной падению напряжения на этом сопротивлении и действующей навстречу току в этой ветви. Для доказательства теоремы выделим из схемы произвольную ветвь с сопротивлением , по которой протекает ток , а всю остальную часть схемы условно обозначим некоторым активным двухполюсником А (см. рис. 6,а). 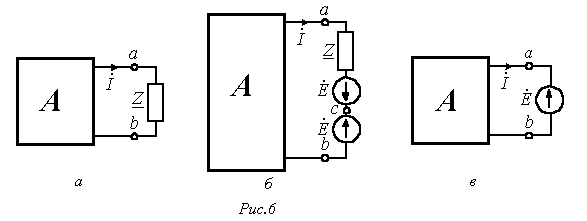 При включении в ветвь с двух одинаковых и действующих навстречу друг другу источников ЭДС с (рис. 6,б) режим работы цепи не изменится. Для этой цепи
Равенство (12) позволяет гальванически соединить точки а и c, то есть перейти к цепи на рис. 6,в. Таким образом, теорема доказана. В заключение следует отметить, что аналогично для упрощения расчетов любую ветвь с известным током можно заменить источником тока . Литература
Контрольные вопросы и задачи
Ответ:
Ответ: ; |
| Теория / ТОЭ / Лекция N 13. Метод эквивалентного генератора. |
| Метод эквивалентного генератора, основанный на теореме об активном двухполюснике (называемой также теоремой Гельмгольца-Тевенена), позволяет достаточно просто определить ток в одной (представляющей интерес при анализе) ветви сложной линейной схемы, не находя токи в остальных ветвях. Применение данного метода особенно эффективно, когда требуется определить значения тока в некоторой ветви для различных значений сопротивления в этой ветви в то время, как в остальной схеме сопротивления, а также ЭДС и токи источников постоянны. Теорема об активном двухполюснике формулируется следующим образом: если активную цепь, к которой присоединена некоторая ветвь, заменить источником с ЭДС, равной напряжению на зажимах разомкнутой ветви, и сопротивлением, равным входному сопротивлению активной цепи, то ток в этой ветви не изменится. Ход доказательства теоремы иллюстрируют схемы на рис. 1. 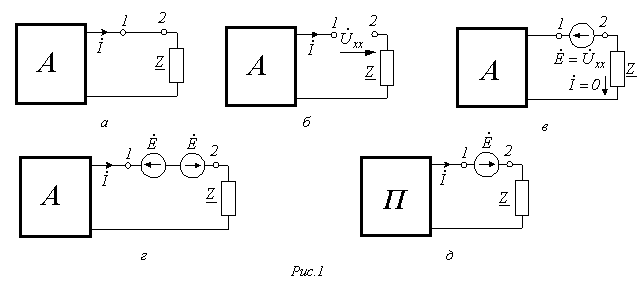 Пусть в схеме выделена некоторая ветвь с сопротивлением Z, а вся оставшаяся цепь обозначена как активный двухполюсник А (рис. 1,а). Разомкнем эту ветвь между точками 1 и 2 (рис. 1,б). На зажимах этой ветви имеет место напряжение . Если теперь между зажимами 1 и 2 включить источник ЭДС с направлением, указанным на рис. 1,в , то, как и в цепи на рис.1,б ток в ней будет равен нулю. Чтобы схему на рис. 1,в сделать эквивалентной цепи на рис. 1,а, в рассматриваемую ветвь нужно включить еще один источник ЭДС , компенсирующий действие первого (рис. 1,г). Будем теперь искать ток по принципу наложения, т.е. как сумму двух составляющих, одна из которых вызывается источниками, входящими в структуру активного двухполюсника, и источником ЭДС , расположенным между зажимами 1 и 2 слева, а другая – источником ЭДС , расположенным между зажимами 1 и 2 справа. Но первая из этих составляющих в соответствии с рис. 1,в равна нулю, а значит, ток определяется второй составляющей, т.е. по схеме на рис. 1,д, в которой активный двухполюсник А заменен пассивным двухполюсником П. Таким образом, теорема доказана. Указанные в теореме ЭДС и сопротивление можно интерпретировать как соответствующие параметры некоторого эквивалентного исходному активному двухполюснику генератора, откуда и произошло название этого метода. Т 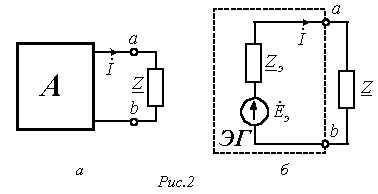 аким образом, в соответствии с данной теоремой схему на рис. 2,а, где относительно ветви, ток в которой требуется определить, выделен активный двухполюсник А со структурой любой степени сложности, можно трансформировать в схему на рис. 2,б. аким образом, в соответствии с данной теоремой схему на рис. 2,а, где относительно ветви, ток в которой требуется определить, выделен активный двухполюсник А со структурой любой степени сложности, можно трансформировать в схему на рис. 2,б.Отсюда ток находится, как:
где - напряжение на разомкнутых зажимах a-b. Уравнение (1) представляет собой аналитическое выражение метода эквивалентного генератора. Параметры эквивалентного генератора (активного двухполюсника) могут быть определены экспериментальным или теоретическим путями. В первом случае, в частности на постоянном токе, в режиме холостого хода активного двухполюсника замеряют напряжение на его зажимах с помощью вольтметра, которое и равно . Затем закорачивают зажимы a и b активного двухполюсника с помощью амперметра, который показывает ток (см. рис. 2,б). Тогда на основании результатов измерений . В принципе аналогично находятся параметры активного двухполюсника и при синусоидальном токе; только в этом случае необходимо определить комплексные значения и . При теоретическом определении параметров эквивалентного генератора их расчет осуществляется в два этапа: 1. Любым из известных методов расчета линейных электрических цепей определяют напряжение на зажимах a-b активного двухполюсника при разомкнутой исследуемой ветви. 2. При разомкнутой исследуемой ветви определяется входное сопротивление активного двухполюсника, заменяемого при этом пассивным. Данная замена осуществляется путем устранения из структуры активного двухполюсника всех источников энергии, но при сохранении на их месте их собственных (внутренних) сопротивлений. В случае идеальных источников это соответствует закорачиванию всех источников ЭДС и размыканию всех ветвей с источниками тока. Сказанное иллюстрируют схемы на рис. 3, где для расчета входного (эквивалентного) сопротивления активного двухполюсника на рис. 3,а последний преобразован в пассивный двухполюсник со структурой на рис. 3,б. Тогда согласно схеме на рис. 3,б 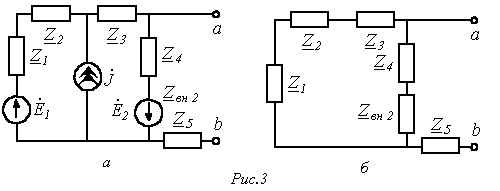 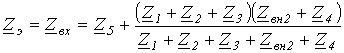 . .В качестве примера использования метода эквивалентного генератора для анализа определим зависимость показаний амперметра в схеме на рис. 4 при изменении сопротивления R переменного резистора в диагонали моста в пределах . Параметры цепи Е=100 В; R1=R4=40 Ом; R2=R3=60 Ом. 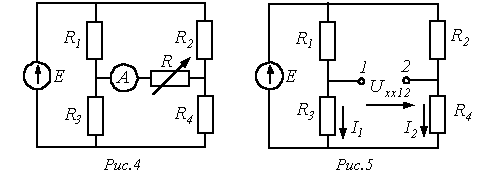 В соответствии с изложенной выше методикой определения параметров активного двухполюсника для нахождения значения перейдем к схеме на рис. 5, где напряжение на разомкнутых зажимах 1 и 2 определяет искомую ЭДС . В данной цепи 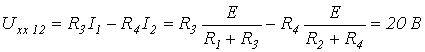 . .Для определения входного сопротивления активного двухполюсника трансформируем его в схему на рис. 6. 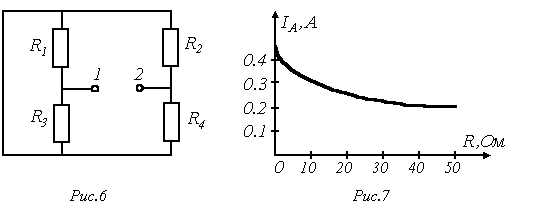 Со стороны зажимов 1-2 данного пассивного двухполюсника его сопротивление равно: 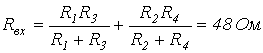 . .Таким образом, для показания амперметра в схеме на рис. 4 в соответствии с (1) можно записать
Задаваясь значениями R в пределах его изменения, на основании (2) получаем кривую на рис.7. В качестве примера использования метода эквивалентного генератора для анализа цепи при синусоидальном питании определим, при каком значении нагрузочного сопротивления в цепи на рис. 8 в нем будет выделяться максимальная мощность, и чему она будет равна. П 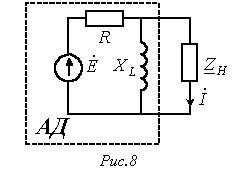 араметры цепи: ; . араметры цепи: ; .В соответствии с теоремой об активном двухполюснике обведенная пунктиром на рис. 8 часть схемы заменяется эквивалентным генератором с параметрами 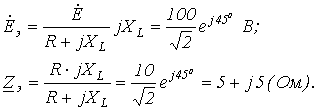 В соответствии с (1) для тока через можно записать 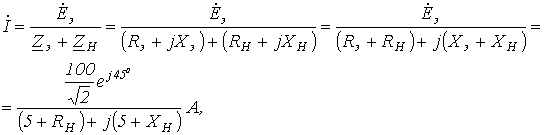 откуда для модуля этого тока имеем 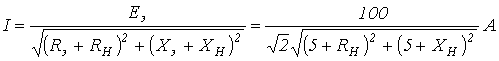 . (3) . (3)Анализ полученного выражения (3) показывает, что ток I, а следовательно, и мощность будут максимальны, если ; откуда , причем знак “-” показывает, что нагрузка имеет емкостный характер. Таким образом, 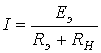 и и 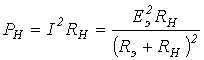 . .Данные соотношения аналогичны соответствующим выражениям в цепи постоянного тока, для которой, как известно, максимальная мощность на нагрузке выделяется в режиме согласованной нагрузки, условие которого . Таким образом, искомые значения и максимальной мощности: Теорема вариаций Теорема вариаций применяется в тех случаях, когда требуется рассчитать, насколько изменятся токи или напряжения в ветвях схемы, если в одной из ветвей этой схемы изменилось сопротивление. Выделим на рис. 9,а некоторые ветви с токами и , а остальную часть схемы обозначим активным четырехполюсником А. При этом, полагаем что проводимости и известны. 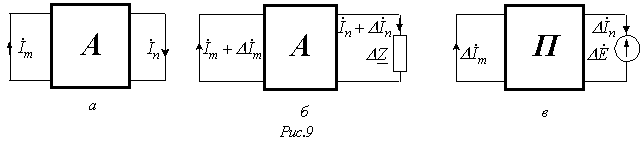 Пусть сопротивление n-й ветви изменилось на . В результате этого токи в ветвях схемы будут соответственно равны и (рис. 9,б). На основании принципа компенсации заменим источником с ЭДС Для этой цепи можно записать 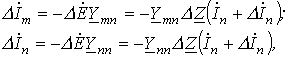 откуда 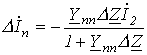 и и 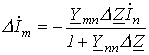 . .Полученные соотношения позволяют определить изменения токов в m-й и n-й ветвях, вызванные изменением сопротивления в n-й ветви. Литература
Контрольные вопросы и задачи
Ответ: .
Ответ: |
| Теория / ТОЭ / Лекция N 14. Пассивные четырехполюсники. |
| При анализе электрических цепей в задачах исследования взаимосвязи между переменными (токами, напряжениями, мощностями и т.п.) двух каких-то ветвей схемы широко используется теория четырехполюсников. Четырехполюсник – это часть схемы произвольной конфигурации, имеющая две пары зажимов (отсюда и произошло его название), обычно называемые входными и выходными. Примерами четырыхполюсника являются трансформатор, усилитель, потенциометр, линия электропередачи и другие электротехнические устройства, у которых можно выделить две пары полюсов. В общем случае четырехполюсники можно разделить на активные, в структуру которых входят источники энергии, и пассивные, ветви которых не содержат источников энергии. Ниже будут рассмотрены элементы теории пассивных четырехполюсников. Для записи уравнений четырехполюсника выделим в произвольной схеме ветвь с единственным источником энергии и любую другую ветвь с некоторым сопротивлением (см. рис. 1,а). 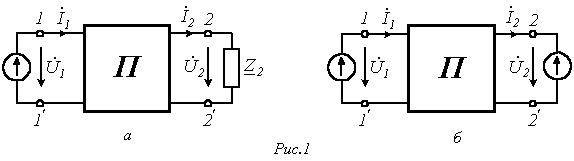 В соответствии с принципом компенсации заменим исходное сопротивление источником с напряжением (см. рис. 1,б). Тогда на основании метода наложения для цепи на рис. 1,б можно записать
Решая полученные уравнения (1) и (2) относительно напряжения и тока на первичных зажимах, получим 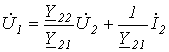 ; ;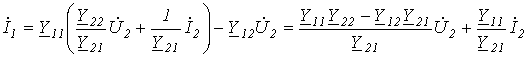 или
где ; ; Учитывая, что в соответствии с принципом взаимности , видно, что коэффициенты четырехполюсника связаны между собой соотношением
|

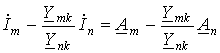 .
. 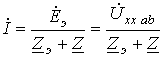 ,
, 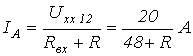 .
. 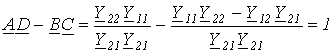 .
.