Лекция 2 Определители. Лекция определители
 Скачать 291 Kb. Скачать 291 Kb.
|
|
Лекция 2. определители
1. Определители второго порядка Понятие определителя вводится только для квадратной матрицы. Определитель – это число, которое считается по определенным правилам. Порядок определителя – это порядок квадратной матрицы. Если для задания матриц использовались круглые скобки, то в теории определителей используют прямые скобки. Каждой квадратной матрице поставим в соответствие некоторое число, которое будем называть определителем матрицы, и укажем правило его вычисления. Обозначения:
Пример 1. 2. Определители третьего порядка
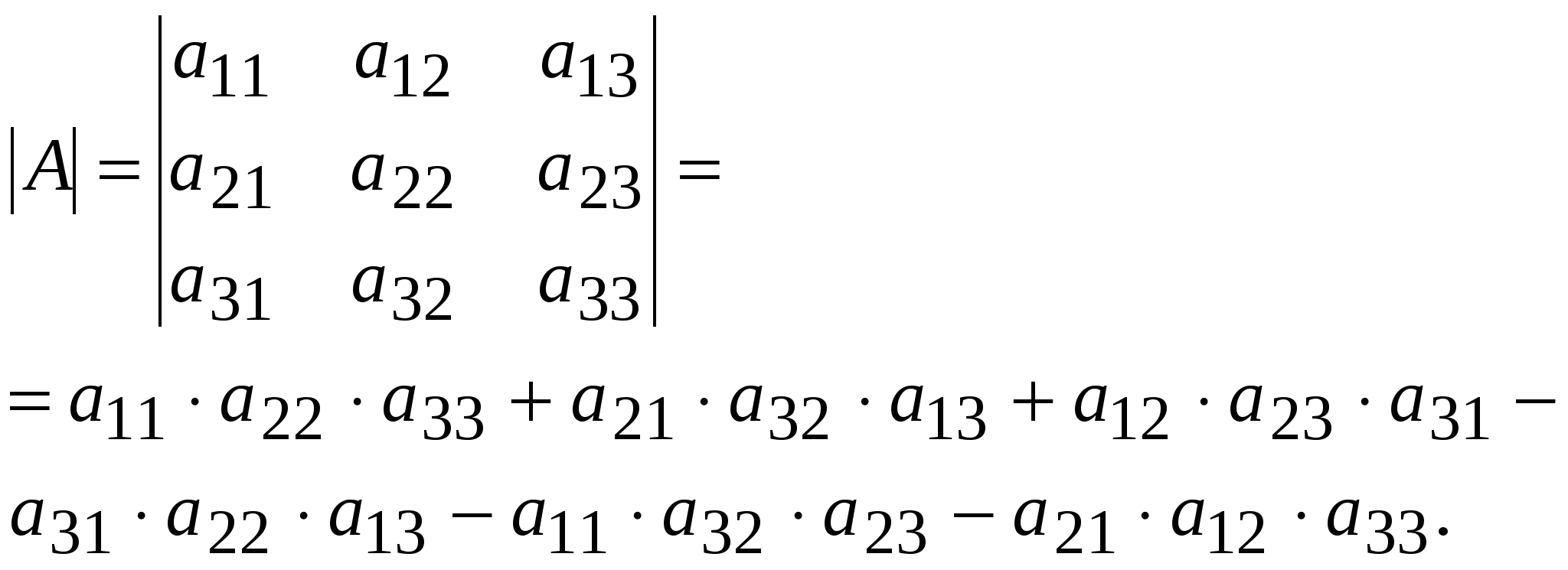 В каждом произведении нет чисел из одного столбца или одной строки. Приведем схему для запоминания порядка получения слагаемых в определителе. 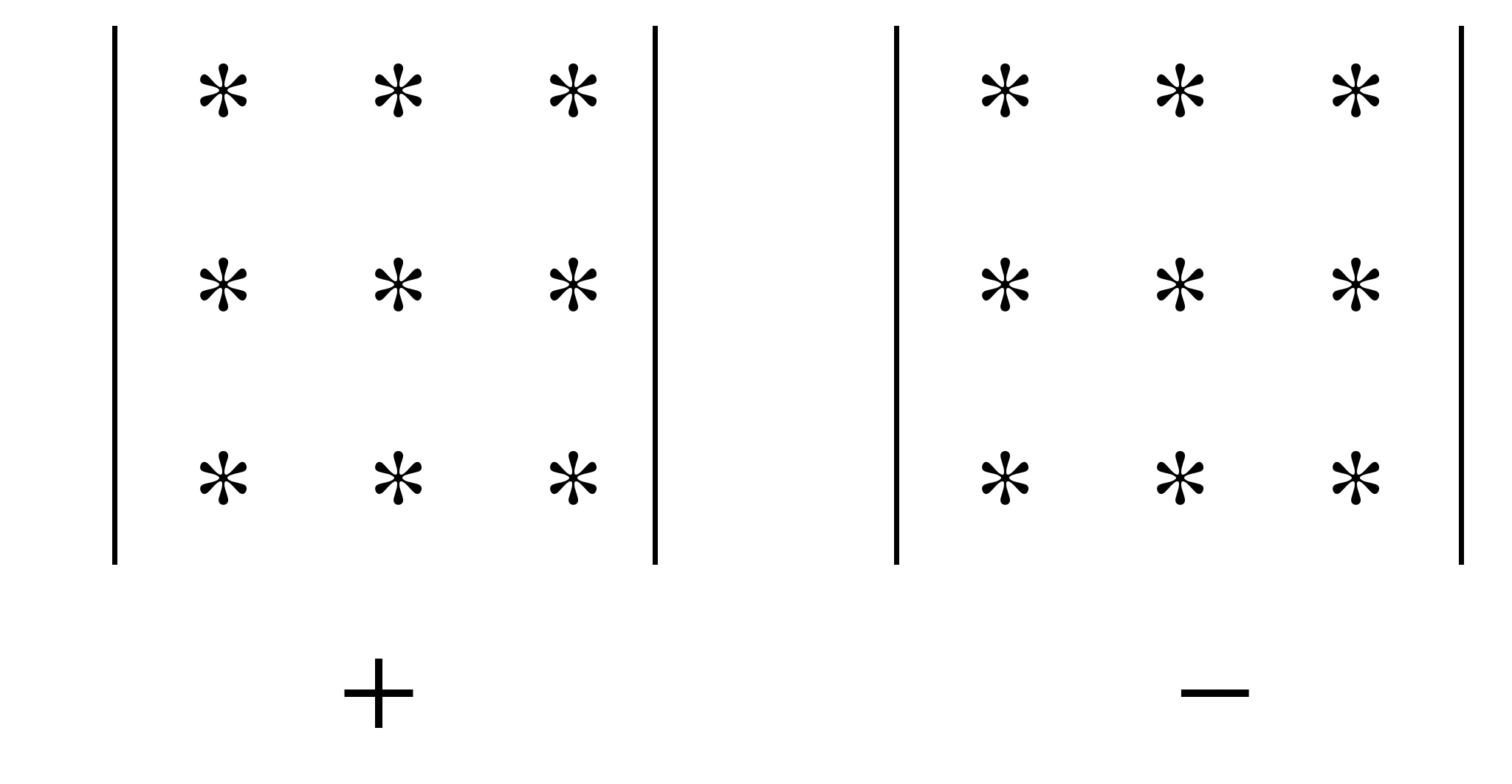   Произведение чисел на одной диагонали берется со знаком «+» (это главная диагональ матрицы), а на другой – с противоположным знаком. Пример 2. 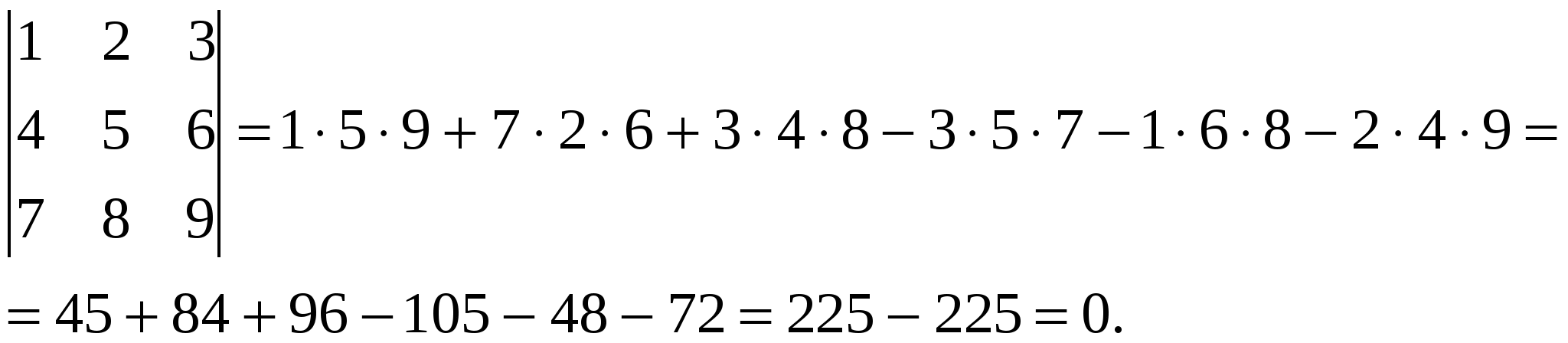 3. Алгебраические дополнения и миноры Для вычисления определителей порядка больше третьего применяют другие способы вычисления.
Пример 3. Минор  есть есть
Полезно запомнить, что Пример 4. В примере 3 алгебраическое дополнение 4. Разложение определителя по строке или столбцу Вычисление определителя
Это число равно сумме произведений элементов любой Пример 5. Вычислить определитель третьего порядка 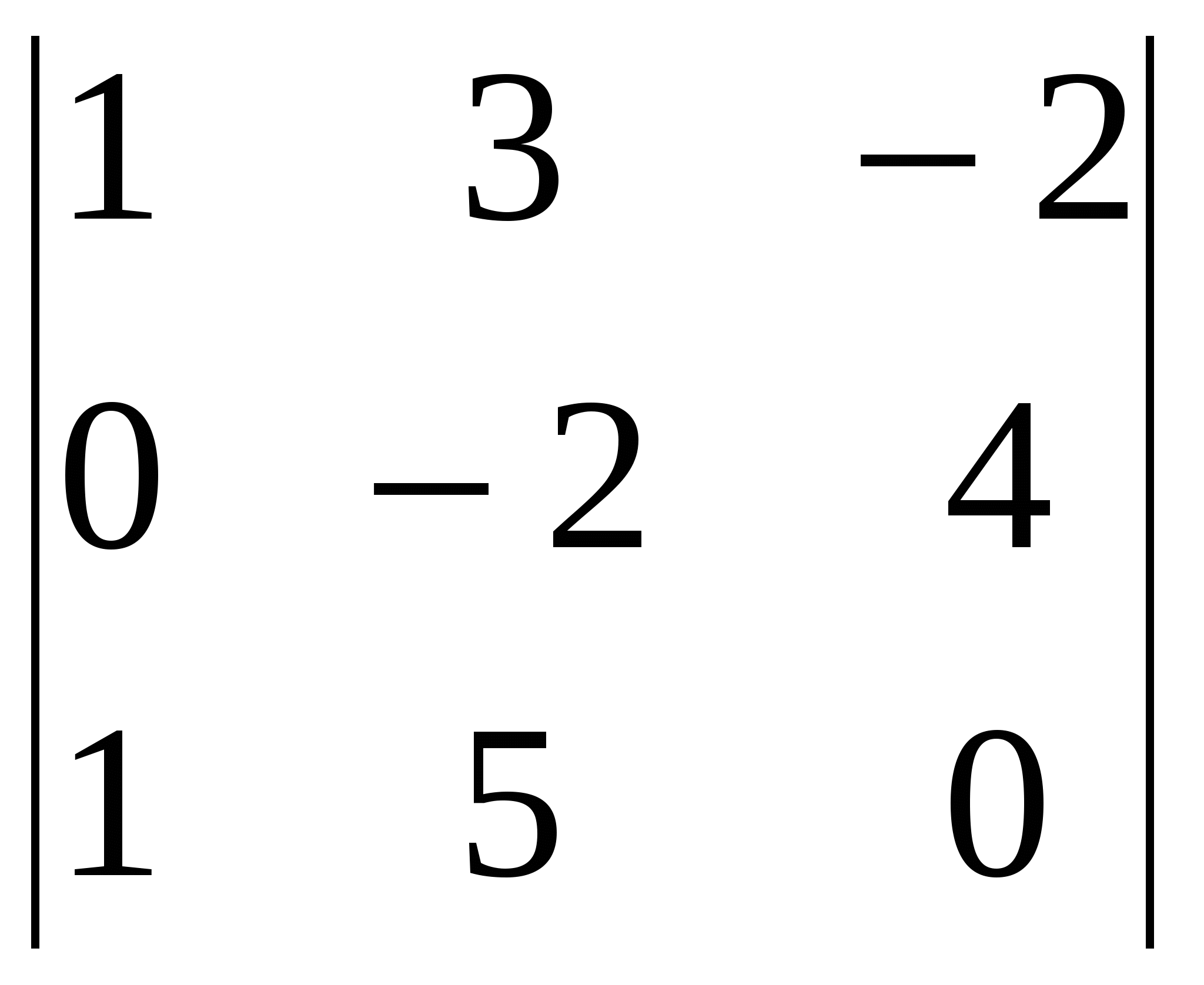 разложением по первой строке. разложением по первой строке. Решение 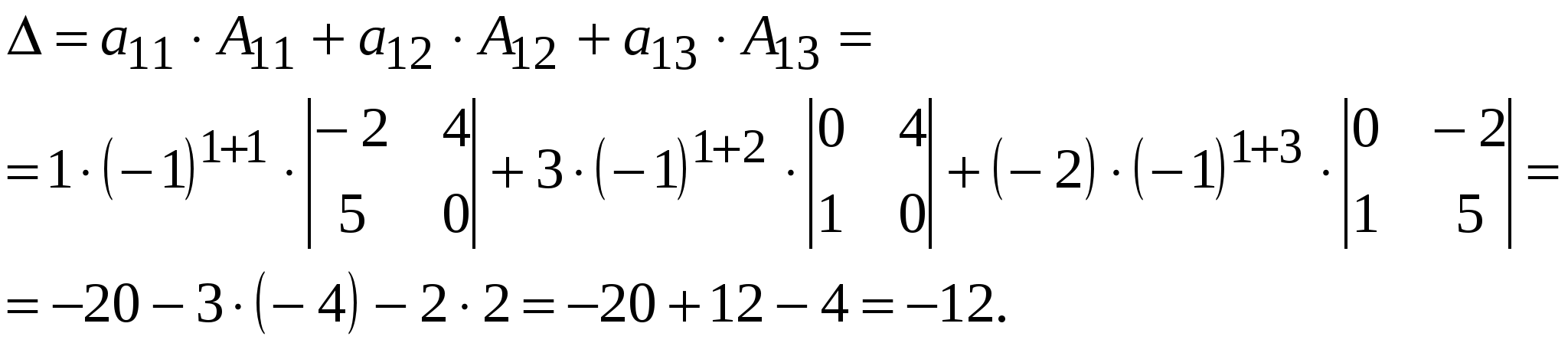
Это число равно сумме произведений элементов любого Независимо от способа разложения всегда получается один и тот же ответ. 5. Свойства определителей 1. При транспонировании квадратной матрицы ее определитель не меняется: Вывод. Свойства определителей, сформулированных для строк, справедливы и для столбцов. 2. При перестановке двух строк (столбцов) определитель меняет знак на противоположный. Например, 3. Определитель равен нулю, если: а) он имеет нулевую строку (столбец) б) он имеет пропорциональные (одинаковые) строки (столбец) 4. Общий множитель в строке (столбце) можно выносить за знак определителя. Например, 5. Определитель не изменяется, если к элементам какой-либо строки прибавить (вычесть) соответствующие элементы другой строки, умноженные на любое число. Например, 6. Если в определителе каждый элемент строки есть сумма двух слагаемых, то этот определитель равен сумме двух определителей: 7. Определитель произведения двух квадратных матриц одного и того же порядка равен произведению определителей этих матриц: 8. Определитель квадратной матрицы треугольного вида равен произведению элементов, стоящих на главной диагонали: 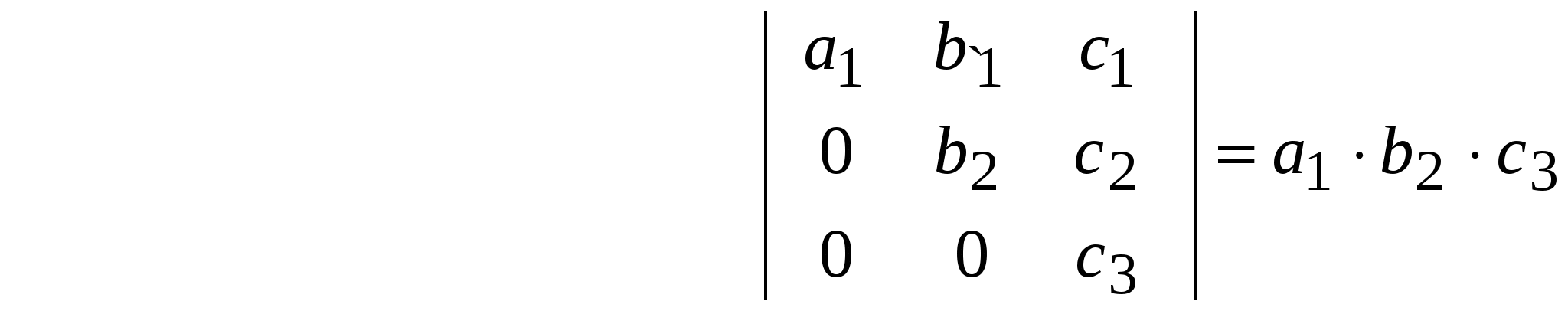  . .6. Обратная матрица Вместо операции деления матриц вводится понятие обратной матрицы.
Обозначается обратная матрица Очевидна аналогия с числами: для числа 2 число ½ есть обратное, так как Теорема «Необходимое и достаточное условие существования обратной матрицы». Для того чтобы квадратная матрица Правило нахождения обратной матрицы 0) Смотрим, является ли матрица квадратной. Если нет, то обратной матрицы не существует; если квадратная, то переходим к пункту 1. 1) Вычисляем определитель матрицы 2) Для каждого элемента матрицы 3) Составляем матрицу из алгебраических дополнений, которая затем транспонируем: 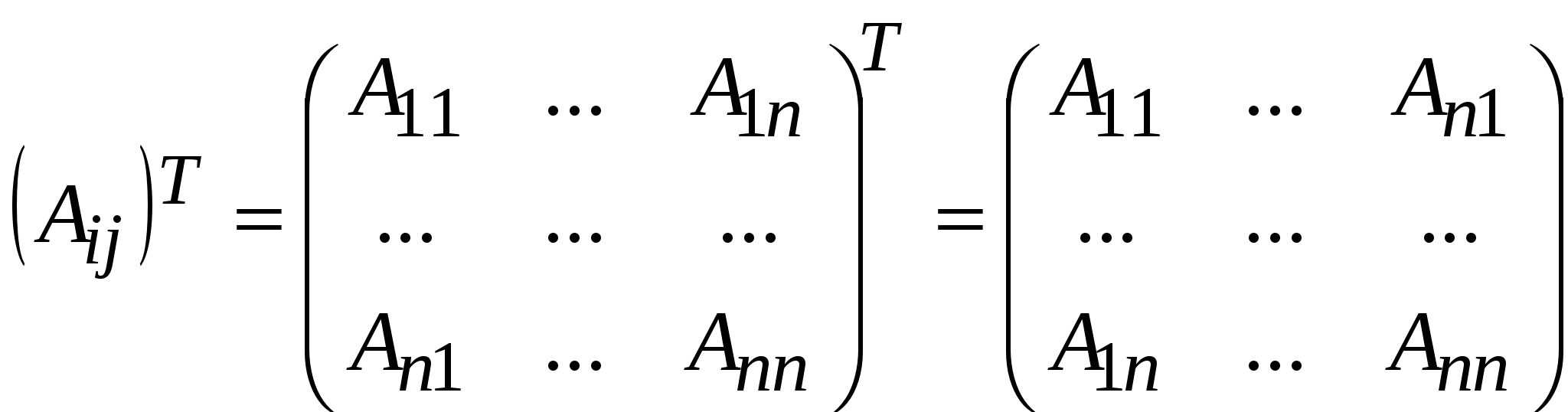 . .4) Каждый элемент матрицы 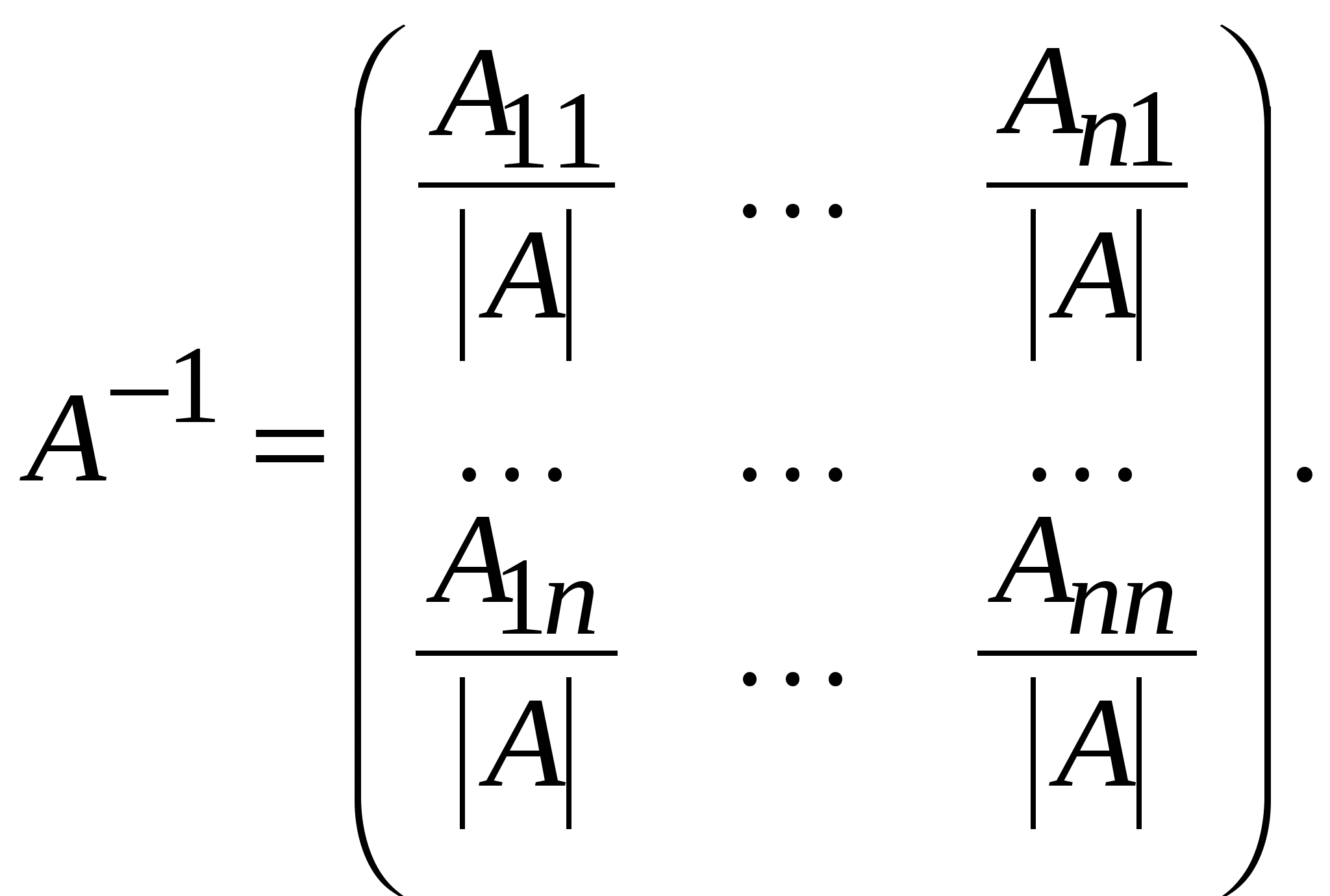 Получаем матрицу, обратную данной. Получаем матрицу, обратную данной.7. Нахождение обратной матрицы для матриц второго порядка Пример 6. Дана матрица Решение. 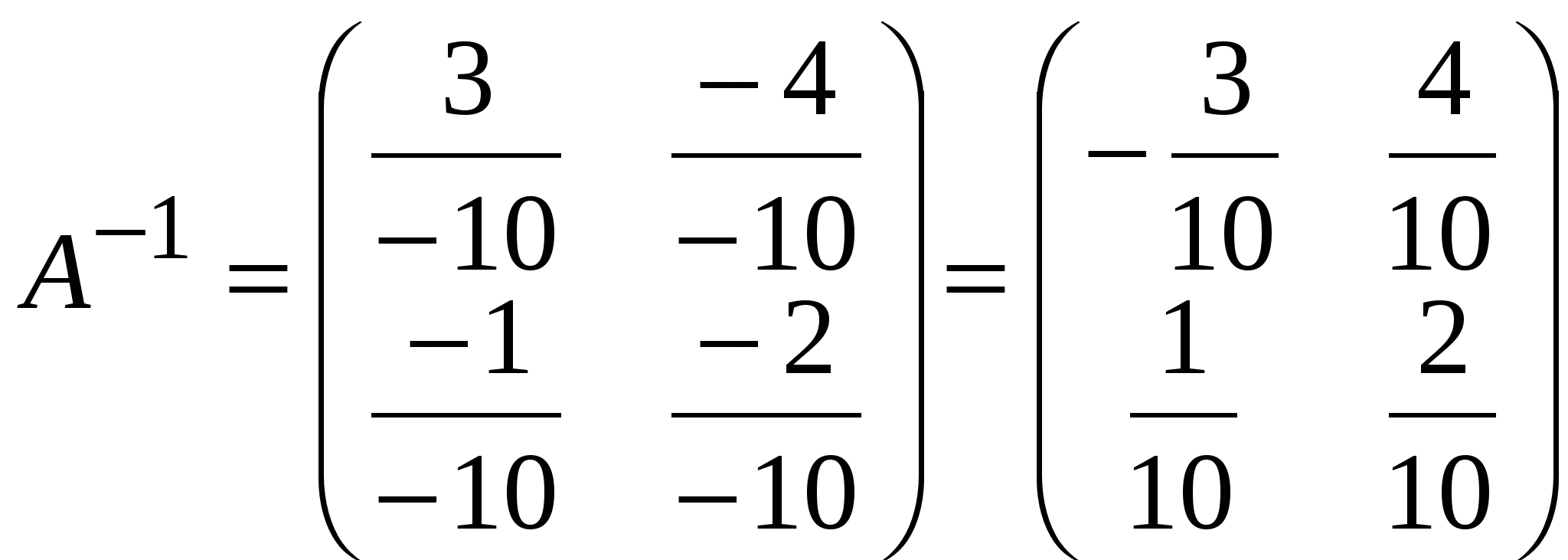 Проверка. Убедимся, что найдена действительно обратная матрица. Найдем произведение матриц 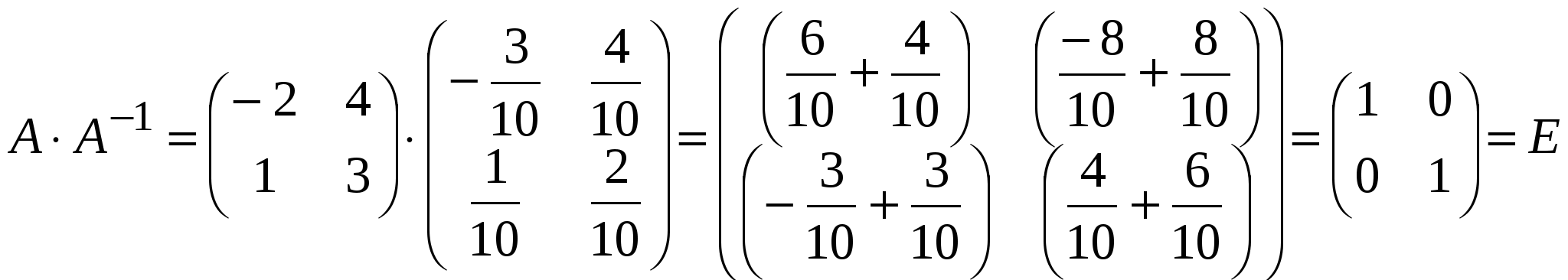 8. Свойства обратной матрицы 1. где А и В – невырожденные квадратные матрицы одинакового порядка. 2. 3. 4. Контрольные вопросы
|

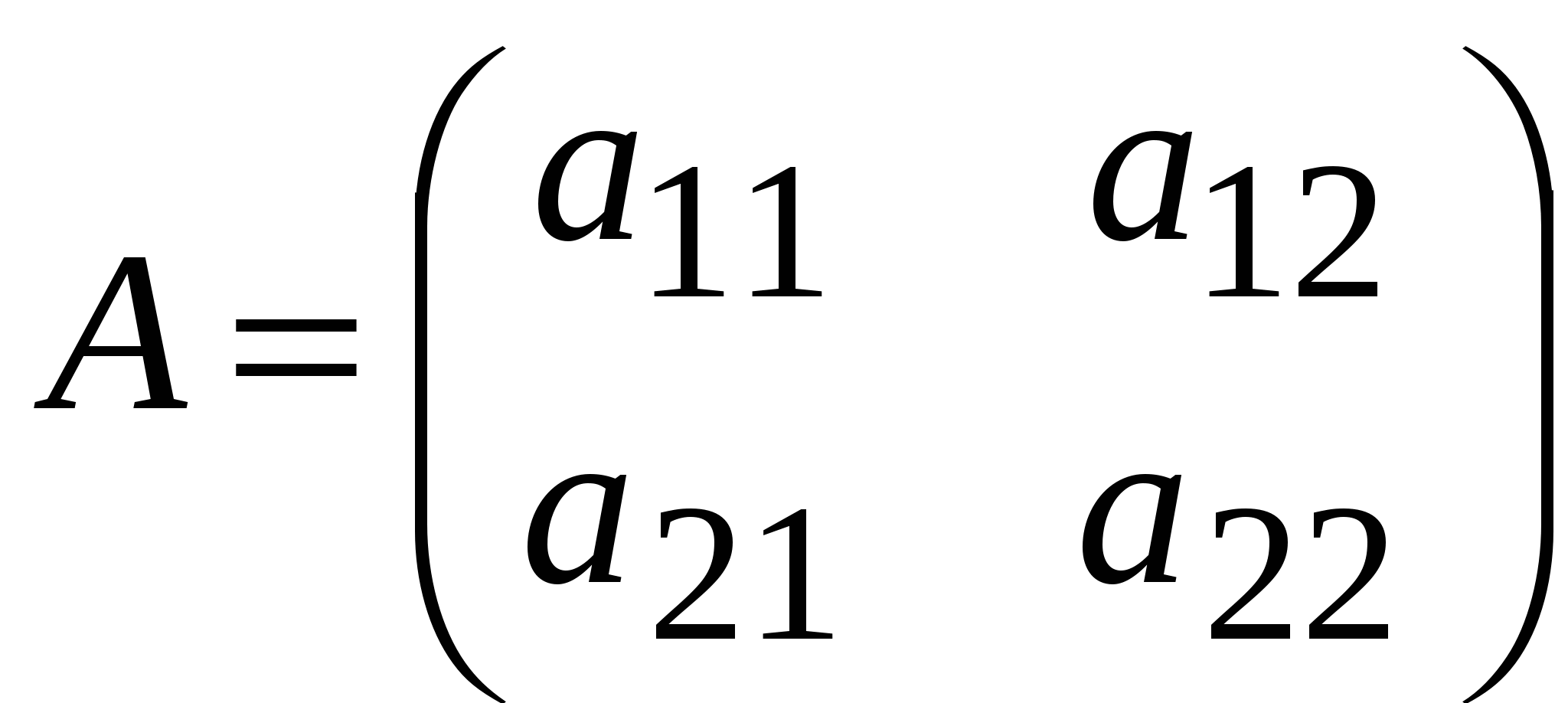 . Определителем второго порядка называется число, вычисляемое по правилу:
. Определителем второго порядка называется число, вычисляемое по правилу: 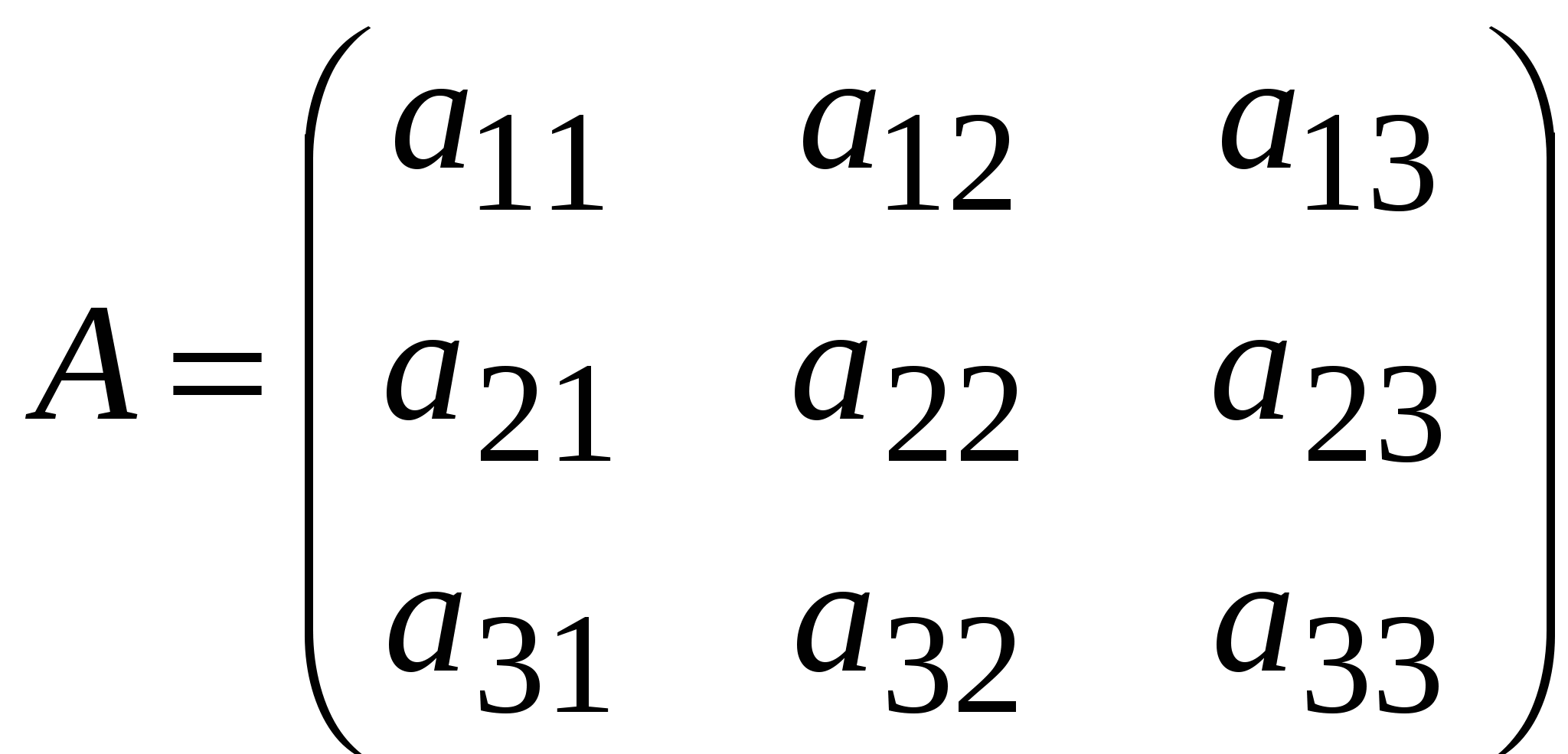 . Определителем третьего порядка называется число, вычисляемое по правилу:
. Определителем третьего порядка называется число, вычисляемое по правилу: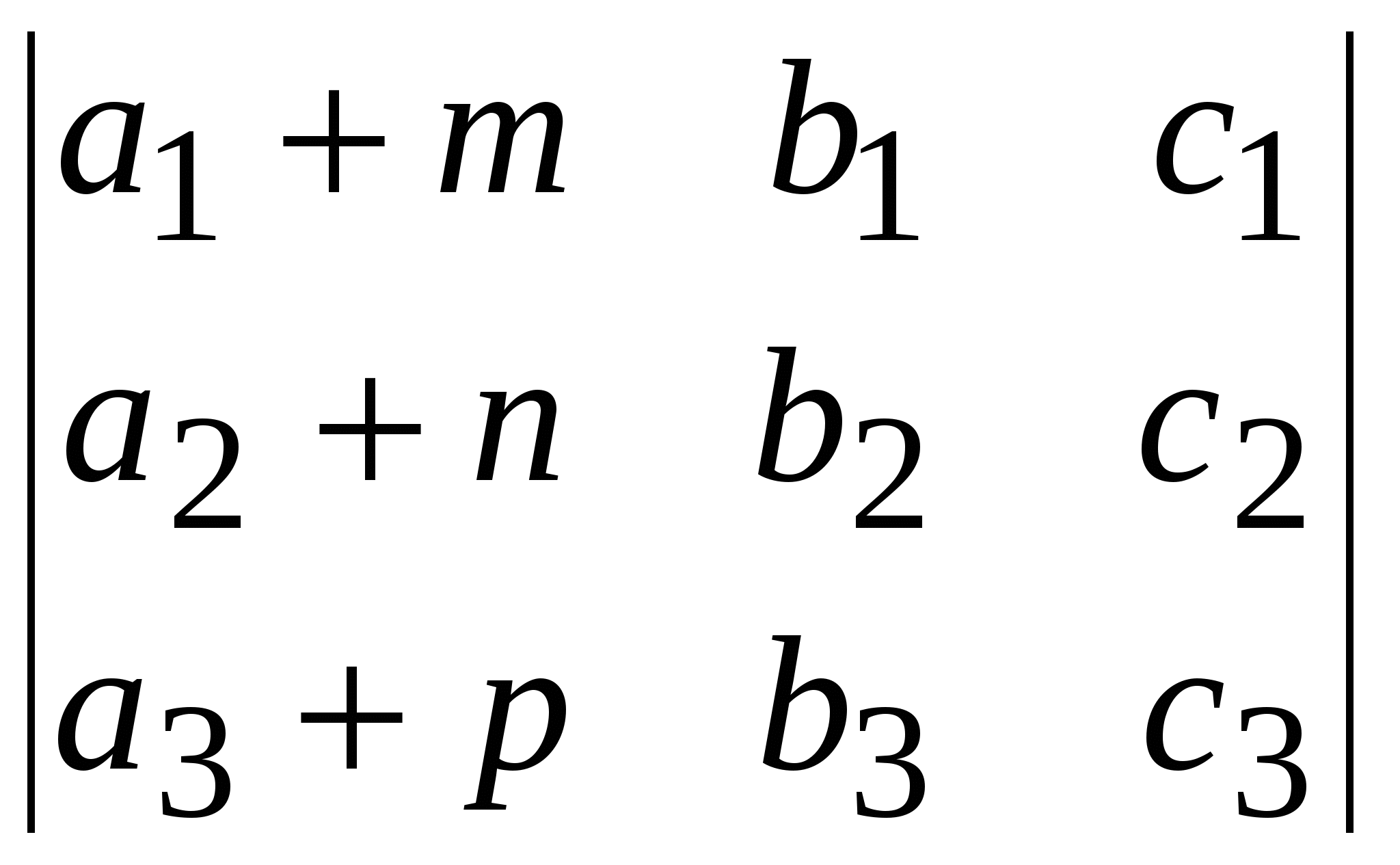 в виде суммы двух определителей.
в виде суммы двух определителей.