|
|
2_понятия и определения. Лекция Основные понятия графов, элементы графов
                     Лекция 2 . Основные понятия графов, элементы графов Лекция 2 . Основные понятия графов, элементы графов
и их определения
ГрафомG=(V,X)называется пара двух конечных множеств: множество точек и множество линий, соединяющих некоторые пары точек.
Точки называются вершинами (узлами) графа, линии – ребрами графа.
Если задан граф G= (V,X),тоV–конечное непустое множество его вершин, X– множествоего ребер.
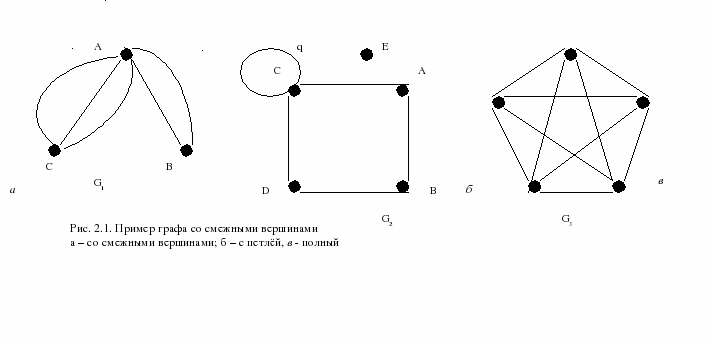
Примеры графов:
г
G4
Пусть дан граф G= (V,X), где V ={A,B,C,D…} - конечное непустое множество его вершин, X(A,B) –его ребра.
Порядок графа - это число вершин в графе.
Размер графа - это число его рёбер.
Ребро называется инцидентнымпо отношению к тем вершинам, которые оно соединяет.
Две вершины графа на�зываются смежными,если существует инцидентное им ребро.
Два ребра называются смежными,если они имеют общую вершину.
Ребро называется петлёй, если его начало и конец совпадают.
A
Задача 1: дан граф G
Х4
Х2
Х3
Х1
B
D
C
Множество вершин - V ={A,B,C,D}
Множество инцидентных ребер – X1(A,D), X2(A,B), X3 (B,C)
Смежные вершины – A и D, A и B, B и C
Смежные ребра X1 и X2, X2 и X3
Ребро-петля X4(С,С)
Порядок графа – 4
Размер графа - 4
Ребра, соединяющие одну и ту же пару вершин, называются кратными или параллельными ребрами.
Количество одинаковых пар вида X(A,B) называется кратностью ребра (A,B).
Степенью вершины называется число, равное числу ребер, инцидентных этой вершине. Степень вершины обозначается символом обозначается deg(A) (от англ.degree - степень).
Если вершине инцидентна петля, то степень ее равна двум: оба конца такого ребра приходят в эту вершину.
Вершина называется изолированной, если степень ее равна нулю.
Граф называется нуль-графом, если он состоит из изолированных вершин.
Вершина графа называется висячей, если степень ее 1.
Задача 2: дан граф G
Множество вершин - V ={A,B,C,D,E,F}
Множество инцидентных ребер – X1(A,B) X2(A,B), X3(C,E), X4(C,D), X5(C,C), X6(D,B) X7(D,F)
Смежные вершины – A и C , A и B, B и D, C и D, D и F.
Смежные ребра X1 и X3, X1 и X6, X2 и X3, X2 и X6, X4 и X6, X4 и X3, X7 и X4, X7 и X6
E
Х5
E
A
C
Х21
Х1
Х4
Х3
Х7
D
Х6
В
Ребро-петля X5(С,С)
Кратные ребра X1(A,B) X2(A,B).
Кратность ребра AB равна 2.
Изолированная вершина Е.
Висячая вершина F.
Степени вершин: Deg(A)=3, Deg(B)=3, Deg(C)=4, Deg(D)=3, Deg(E)=0, Deg(F)=1
Размер графа – 7
Порядок графа - 6
Теорема1. В графе G(V,X) сумма степеней всех его вершин – число четное, равное удвоенному числу ребер графа.
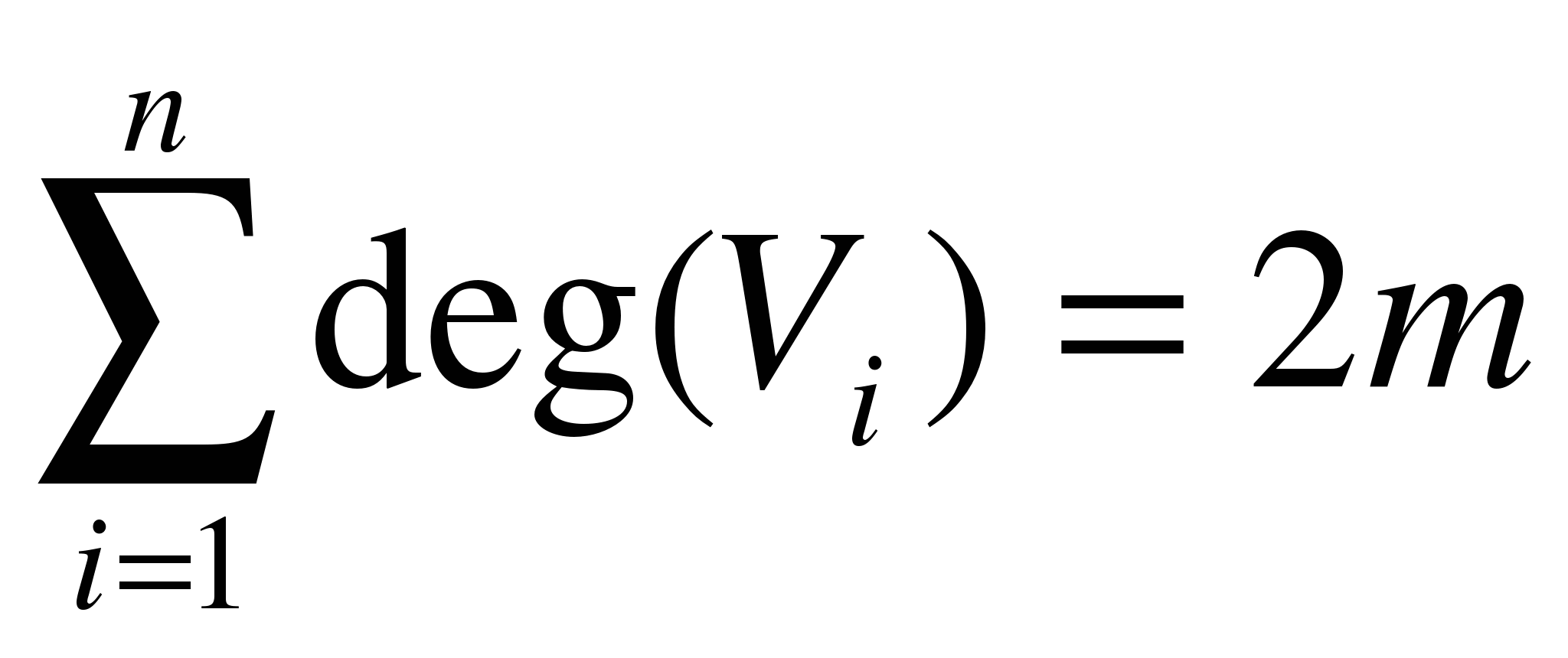
где n- число вершин; m - число рёбер графа.
Пример. Пусть граф содержит 5 ребер, тогда степень этого графа равна r=5·2=10
Вершина называется четной, если ее степень есть четное число и нечетной, если степень ее есть нечетное число.
Теорема 2.Число нечетных вершин любого графа – четно.
Следствие.Невозможно начертить граф с нечетным числом нечетных вершин.
Задача 3. В графе G(V,X) определить: висячие вершины; число ребер; -
доказать, что Теорема 1 верна на данном примере. Проверить теорему 2 на данном примере
C
D
F
H
G
E
B
A
V={A,B,C,D,E,F,G,H}
Висячие: A, B, E, G, H
число ребер m=7
Нечетные вершины:
Deg(A)=1, Deg(B)=1, Deg(E)=1, Deg(G)=1, Deg(F)=3, Deg(H)=1
Четные вершины:
Deg(C)=4, Deg(D)=2
∑ Deg(Vi)=1*5+3+4+2=14, а число ребер m= 7. По теореме1 ∑ Deg(Vi)=2* m, т.е. 2*7=14. Теорема верна.
Число нечетных вершин 6 – четное число.
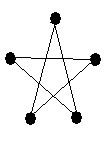
Граф G называется полным, если любые две его различные вершины соединены одним и только одним ребром.
Пример
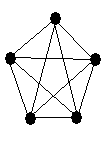
Задача 4. Изобразить полный граф G(V,X), где: V=3;4;6. Определить количество ребер каждого графа и степени вершин.
Таким образом, полный граф определяется только своими вершинами. Пусть число вершин полного графа равно n. Тогда степень любой вершины Deg(V)=n-1. Это понятно из примера, т.к. каждая вершина соединяется с остальными.
Теорема 3Число ребер в полном графе порядка  равно равно  . .
Доказательство
Из каждой вершины в полном графе выходит  ребро. Всего вершин ребро. Всего вершин  штук, но, чтобы не считать каждое ребро дважды, нужно разделить произведение штук, но, чтобы не считать каждое ребро дважды, нужно разделить произведение  на два. на два.
Дополнением графа 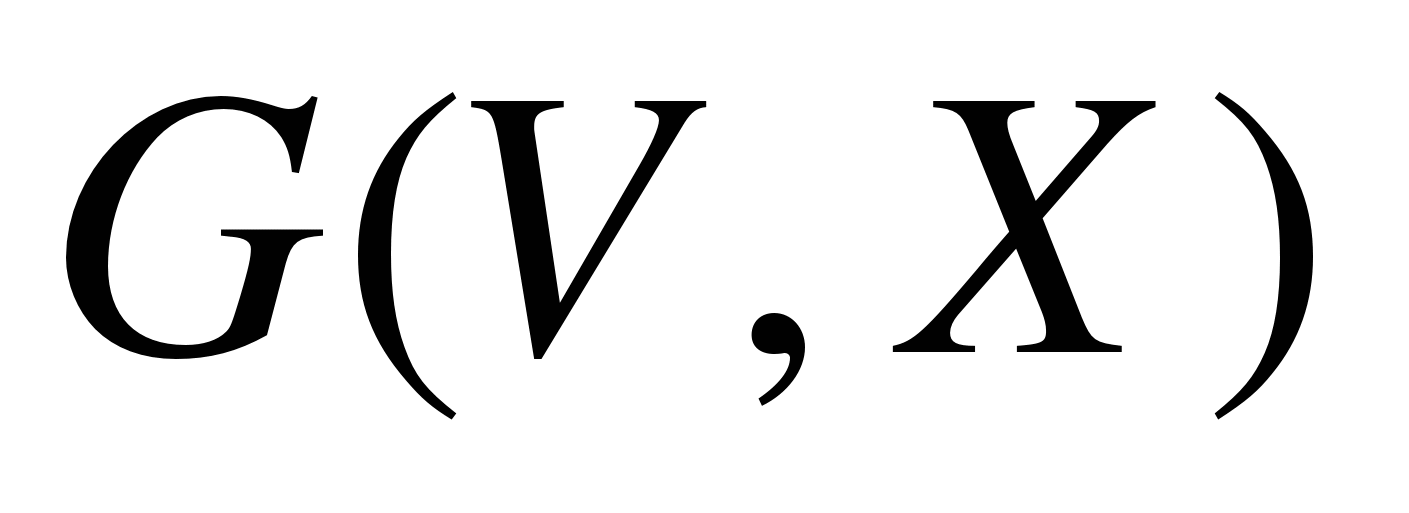 называется граф называется граф 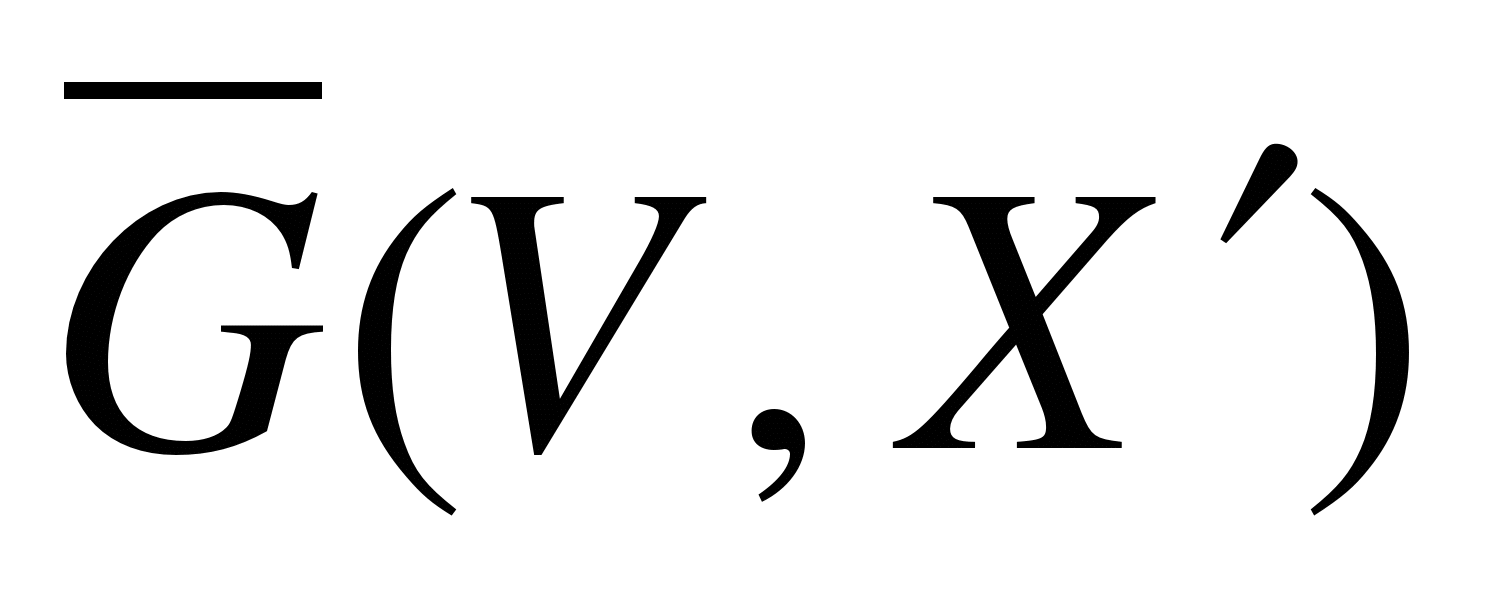 с теми же вершинами V, что и граф G, и имеющий те и только те рёбра с теми же вершинами V, что и граф G, и имеющий те и только те рёбра 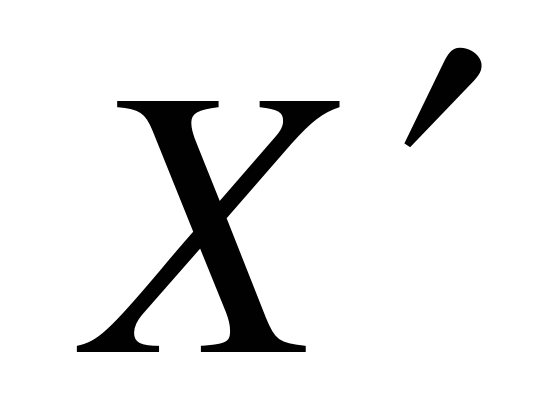 , которые необходимо добавить к графу G, чтобы он стал полным. , которые необходимо добавить к графу G, чтобы он стал полным.
Пример. Дан граф G1. Изобразить его дополнение до полного графа G2 
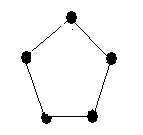
G2
G1
G1
Следствие. Дополнением полного графа будет являться нуль-граф и наоборот. |
|
|
 Скачать 112.91 Kb.
Скачать 112.91 Kb.