количественные отношения. Лекция Освоение детьми количественных отношений, чисел и цифр
 Скачать 63.89 Kb. Скачать 63.89 Kb.
|
|
§ 2. Способы сравнения множеств детьми разного возраста Влияние пространственных факторов на восприятие множества детьми дошкольного возраста. Маленькие дети очень рано начинают сравнивать численности множеств, определяя боль меньшую из них, когда у них возникает в этом реальная необходимость. Например, мать дала старшему сыну три конфеты, а младшему (1 год 6 мес.) лишь две такие же. Малыш, зорко взглянув на конфеты брата, тянется к ним, выражает свое недовольство. Как он узнал, что у брата конфет больше, чем он руководствовался, сравнивая множества? Три конфеты занимают большую площадь, чем две конфеты, если они одинакового размера,-— это один признак. Малыш может поэлементно сравнить конфеты и обнаружить, что у него недостает одной,— это другой способ сравнения. Но попробуйте разместить две конфеты на большей площади, а три — на меньшей, и ребенок уже сбит со своей позиции, склонен думать, что он неправ в своих притязаниях. Исследования, проведенные Н. А. Менчинской, А. М. Леушиной и другими, убеждают, что на восприятие множеств оказывают влияние различные качественно-пространственные факторы. При несвоевременном развитии умений четко вычленять элементы множества у детей часто создается привычка оценивать «величину» множества не по количеству образующих его элементов, а по разным пространственно-качественным признакам, например, по размерам образующих его элементов, по величине площади, занимаемой множеством. Эта тенденция у некоторых детей сохраняется даже в младшем школьном возрасте. Однако с возрастом стремление определять величину множества по пространственно-качественным признакам уменьшается, но оно сохраняется достаточно длительно, потому что количественная сторона остается еще долгое время слабодифференцированной, если на это не обращается внимания. Отсюда следует вывод: важно своевременно развивать у детей умение дифференцировать элементы множества, не ограничиваясь лишь восприятием его как структурно-целостного единства, и еще в дочисловой период учить детей производить сравнение численностей множеств путем практического установления соответствия между их элементами. О способах обучения поэлементному сравнению множеств и умению видеть все элементы множества Выше указывалось, что при воспроизведении линейно расположенного множества дети на накладывают пуговицы, заполняя пространство сравнению между конечными его элементами, но не в равном количестве. Чтобы научить детей правильно воспроизводить множество, изображенное на карточке, необходимо, чтобы они видели каждый элемент совокупности и, пользуясь приемом наложения, воспроизводили данное множество. Исследования и массовый опыт убедительно показали, что уже детей двух-трех лет можно научить приему наложения предметов одной совокупности на рисунки предметов другой совокупности. Детям предлагалась карточка с тремя — пятью нарисованными в ряд пуговицами, указывался прием движения правой рукой слева направо. Дети повторяли это движение на своей карточке, как бы обследуя данное направление. Затем им указывалось, что пуговицами надо закрыть все рисунки, не пропуская ни одного. Этот прием оказался вполне доступным детям уже на третьем году жизни, а в некоторых случаях даже на втором году (1 год 6 мес.). Особую роль при этом играет последовательность движения руки и следящих за нею и рисунками глаз ребенка. То и другое способствует развитию видения элементов множества. В результате подобных упражнений все дети к трем годам свободно овладевают приемом наложения и воспроизводят множество соответственно предъявленному им образцу (см. гл. IX). Следующим приемом, еще более значимым для развития умений воспринимать количественную сторону элементов множества, является прием приложения. Однако предварительное изучение возможностей детей в усвоении этого приема вскрыло ряд его особенностей. Прием приложения более сложный для детей, чем прием наложения, так как он требует более четкой дифференцировки элементов внутри множества и большей самостоятельности. Дети, которые хорошо овладели приемом наложения, испытывают значительные затруднения, когда им предлагается на нижней полоске под нарисованными на карточке пуговицами разложить такое же количество пуговиц, что на образце. Малыши до двух лет шести месяцев раскладывают пуговицы, прижимая их друг к другу и не обращая внимания на количество, нарисованное на карточке. Даже на четвертом году жизни из детей, хорошо владеющих приемом наложения, примерно лишь одна треть пользуется приемом приложения. Испытывают затруднения в овладении этим умением даже дети на шестом году жизни (рис. 2). Рис. 2. Как же ведут себя дети при наличии множества, расположенного не линейно, а в виде числовой фигуры? Дети до трех лёт почти не принимают этого задания, если даже инструкция сопровождается показом того, как надо делать. Часть детей трех лет все же пытается подложить пуговицы, но делает это своеобразно: они выкладывают пуговицы вокруг всей карточки, при этом тесно прижимают их друг к другу (рис. 3). Между тем почти все дети владели приемом наложения. Рис. 3. Следует отметить, что малышей затрудняет не только сам прием, но и смысл слов подложить, приложить (некоторые дети прятали взятые ими пуговицы под карточку). Отсюда следует вывод, что детям второго и третьего года жизни необходимо практически разъяснять различия смысла слов наложить, приложить, подложить. Рис. 4 Рис. 5 Даже старшие дети (пять лет), выполняя задание уложить на полоске столько пуговиц, сколько их было в числовой фигуре, раскладывают их или вокруг четырех сторон квадрата, или вокруг трех сторон, или по двум сторонам, или конструируют форму числовой фигуры прямо на столе, причем не в равном количестве (рис. 4 и 5). Внимание детей сосредоточивается на самом способе нового действия приложения, а восприятие количества вытесняется. В чем же общая причина затруднений в овладении способом приложения элементов одного множества к элементам другого и почему именно этот способ является наиболее значимым в формировании количественного восприятия множества? Чтобы подложить в совокупности пуговиц одну пуговицу под другой, необходимо дифференцировать пространственные отношения между всеми элементами множества, точно воспринять их количество как при линейном расположении, так и в виде числовой фигуры. Почему же дети сравнительно легко овладевают приемом наложения при восприятии тех же множеств? Решая задание способом наложения, ребенок накладывает пуговицу на ее изображение, закрывает ее, и ведущими для него являются сами изображения; пространственные же отношения между нарисованными пуговицами не играют в решении данного задания еще существенной роли, и ребенок не замечает их. Ему важно последовательно закрыть все рисунки совокупности. Таким образом, прием наложения способствует, с одной стороны, формированию представления о множестве как структурно замкнутом целом, а с другой — усиливает внимание детей к тому, что множество состоит из отдельных элементов. Общее же количество элементов еще мало интересует ребенка. В чем же причина затруднений при подкладывании элементов, какие новые задачи возникают перед ребенком при овладении данным способом? Ребенку надо точно воспроизвести то количество элементов, которое образует данное множество. Для этого необходимо воспринять не только изображения пуговиц, но и пространственные отношения между ними. Только при этом условии можно выделить количественную сторону множества. Учитывать же расстояния между изображениями ребенок еще не научился. Если при наложении ребенок руководствуется самим изображением, то для использования приема приложения он должен подняться на новый уровень восприятия множества — научиться видеть пространственные отношения между рисунками, т. е. элементами внутри множества, что подведет его к точному количественному их восприятию. Не владея еще умением анализировать пространственные отношения между элементами как при линейном их расположении, так и в числовой фигуре, ребенок заполняет площадь в границах множества, тесно прижимая пуговицы друг к другу, а тем самым воспроизводит неадекватное образцу количество. И если в процессе обучения на пространственную дифференцировку элементов внутри множества не обращается должного внимания, то отсутствие такой дифференцировки влечет за собой значительные ошибки в восприятии количественной стороны совокупности даже на том этапе, когда ребенок, казалось бы, научился считать с помощью слов-числительных. Приведем один из многочисленных примеров такого поведения. Юра П. 5 лет 1 мес. Юра свободно называет числительные до 13. На предложенной карточке он считает семь пуговиц, расположенных в ряд, затем отсчитывает пуговицы по одной, укладывая их в ряд на нижней полоске, не руководствуясь, однако, тем, чтобы пуговицы точно располагались под их рисунками 1:1. Положив шесть пуговиц, Юра останавливается, считая задание законченным, поскольку он заполнил, как ему кажется, всю площадь в границах множества. Когда по просьбе воспитательницы он пересчитывает оба множества, то обнаруживает свою ошибку, так как не слышит соответствия при назывании последних числительных в обоих множествах. В процессе пересчитывания Юра случайно несколько отодвинул пуговицы. Увидев свободное место под последней пуговицей образца, он еще теснее сдвинул их и добавил еще две пуговицы. Уже по собственной инициативе Юра пересчитал снова обе совокупности и вновь убедился в том, что сделал неверно. «Не так»,— говорит Юра. Он вновь еще теснее сдвигает пуговицы, добавляя одну. На образце семь пуговиц, а у него девять. Пересчитав снова, говорит: «Неверно у меня. Не получается что-то, еще передвинуть надо». Сдвинув еще теснее, он добавил еще одну, десятую, пуговицу и вновь убедился, что сделал неверно. «Что-то опять не получается. Вот работу потруднее дали. Но ведь получится как-то». Попытку помочь Юра решительно отверг: «Я сам. Потруднее работу дали, чтобы гадать. Как же это?» — раздумывает Юра. «А ты попробуй наложить пуговицы на кружки»,—советует все же педагог. Юра воспользовался советом. «Семь! — обрадовался он.— Вот сколько лишних я взял. Не получилось. Лишние пуговицы были». Таким образом, только при наводящем указании Юра смог сопоставить элементы одного множества с элементами другого, один к одному. Выполняя задание воспроизвести множество, расположенное в виде числовой фигуры, и трансфигурировать его линейно, Юра сосчитал на карточке пять пуговиц затем взял пуговицы по одной, не считая, и разложил по две пуговицы по трем сторонам квадрата: верхней, правой и нижней. Юра внимательно смотрит на выложенные им пуговицы, сопоставляет их одна с другой, рассуждает при этом вслух: «Эта к этой, эта не к этой идет, а к этой» и т. д., потом снимает одну пуговицу и пересчитывает оба множества. Но он не слышит при счете в последних называемых числительных соответствия. «Как же это правильно сделать?» Вновь сопоставляет элементы один к одному. «Эта к этой, эта к этой (пауза), так, эта не к этой идет, а к этой»,— рассуждает вслух Юра. Вновь все считает и радостно заявляет: «Здесь пять и здесь пять, теперь верно». Итак, Юра не усвоил еще подлинного значения счета; он знает лишь одно: равенство множеств бывает тогда, когда последние числительные при их назывании совпадают, а когда он не слышит этого совпадения, считает, что допустил какую-то ошибку, но в чем она состоит, для него остается неясным. Это можно продемонстрировать еще на одном примере. 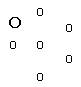 Рис. 6. Юра считает семь кружков, выложенных на карточке, как показано на рис. 6, и ошибается, говоря «шесть». «Ты неверно считал».— «Нет, все верно»,— возражает Юра, однако вновь пересчитывает: «Ой, нет, не все верно. Семь». Юра начинает раскладывать пуговицы вокруг формы, но педагог напоминает ему, что надо раскладывать в ряд. Юра кладет пуговицы одна за другой, называя числительные, но считает не пуговицы, а свои движения. Например, положив четвертую пуговицу в ряд, говорит «пять», так как, взяв ее из коробки, сказал «четыре». Выложив еще одну пуговицу и назвав число шесть, Юра говорит: «Все», считая задание выполненным; он уже забыл количество пуговиц на карточке. «Посчитай, верно ли ты положил». Юра считает кружки на карточке, но пропускает один и говорит, что кружков шесть. Снова пересчитав, он находит, что их семь: «Семь, а эту я забыл. Ой, чего это я все забываю!» Еще раз считает рисунки пуговиц и убеждается, что их семь. «Семь»,— утверждает он и начинает считать выложенные им пуговицы. «Шесть,— говорит он,— опять неверно». Подумав, добавляет одну пуговицу и заявляет довольный: «Теперь уже семь. Вот какую трудную задачу даете». На что же следует обратить особое внимание, анализируя поведение детей? Счетом дети пользуются не как средством определения количества элементов множества: называя числительные по порядку, они ждут, когда появится в этой цепочке слово-числительное, то, которое будет соответствовать по звучанию числительному, названному при счете другой совокупности. Тем самым число для этих детей не является еще показателем количества элементов множества. Констатируя при пересчитывании двух множеств их несоответствие, дети обнаруживают его лишь по разноименному звучанию последних слов-числительных. Дети эти не владеют еще в подлинном смысле деятельностью счета как деятельностью установления взаимно-однозначного соответствия между предметами и числами натурального ряда. Они легко сбиваются при счете, небрежно соотносят слова-числительные с объектами совокупности: то пропускают слова-числительные, то пропускают объекты при счете, то сразу называют два числительных, соотнеся с ними один объект. Дети, казалось бы, проявляют активность в счете, однако они еще не поднялись до уровня понимания значения счета. Приведенный пример свидетельствует, что дети преждевременно перешли к счетной деятельности с помощью слов-числительных. У них не сформировалось еще четкое восприятие всех элементов множества. Они не научились практически сравнивать множества, сопоставляя их элементы один к одному. Отсутствие этих знаний не позволило им четко усвоить операцию счета «..подняться к более глубокому пониманию значения числа как показателя равночисленности множеств. Естественно, что для этих детей остается неясным и значение последовательности чисел, которую они легко нарушают, поскольку запоминание порядка слов-числительных у них сформировалось лишь на основе речедвигательных ассоциаций. Приведенные факты свидетельствуют об огромной важности и значении формирования представлений о множестве и о различных операциях с множествами еще в дочисловой период обучения. Отсюда следует сделать вывод: необходимо уже с раннего возраста не только учить детей различать «много и один», но и формировать представление о множестве как структурно-целостном единстве, а также четкое восприятие отдельных элементов, образующих множество. Все это и будет подводить ребенка к умению считать элементы множества с помощью слов-числительных. Предварительная работа с множествами позволит детям в последующем скорее и глубже осмыслить понятие числа и овладеть деятельностью счета. Значение операций с множествами в дочисловой период Уже в дочисловой период могут проводиться с множествами различные операции с множествами. Выше указывалось на тенденцию восприятия детьми множества как единого целого, если все его элементы качественно однородны. Если такая тенденция является вполне оправданной в период перехода от восприятия множественности к восприятию множества как структурно-целостного единства (в 2—4 года), то позднее она становится препятствием к дальнейшему развитию. Например, на столе лежат четыре рыбки и в коробке — шесть рыбок. Ребенок шести лет воспринимает их только раздельно. На вопрос, сколько всего рыбок, он отвечает, что, если из коробки выложить на стол и остальные рыбки, их будет десять. Или другой пример: девочка нарисовала по обе стороны реки по два домика. На вопрос, сколько всего домиков по обе стороны реки, она ответила: если эти два домика перенести на другую сторону, тогда их будет четыре. Различное пространственное расположение элементов множества мешает восприятию их в единстве. Поэтому необходимо предлагать детям производить различные операции с множествами: составлять единое множество из двух групп, каждая из которых обладает своими качественными особенностями, несущественными для всего множества в целом. Например, объединить несколько красных и синих флажков в единое множество флажков или, наоборот, разделить единое множество (кружков) на подмножества по тому или иному признаку (цвета, размера, формы, вида и др.). Таким образом, одно и то же множество, составленное по родовому признаку, может быть упорядочено в подмножества по разным признакам. И все эти выделенные подмножества могут сопоставляться, сравниваться друг с другом, при этом выявляться количественные отношения между ними, равенства, неравенства, не выражаемые еще числом. Обследования, проведенные среди первоклассников, показали, что далеко не все дети, перешедшие из детского сада в школу, умеют упорядочивать множества по разным признакам, понимать различные отношения между ними. Из этого вытекает следующий вывод: на протяжении всего дошкольного возраста необходимо работать с детьми над множествами. Особое внимание уделять формированию представлений о множестве как структурно-целостном единстве и в то же время учить видеть каждый отдельный элемент множества. При этом нет необходимости спешить обучать детей счету с помощью слов-числительных. Значительно важнее научить детей приемам поэлементного сравнения двух множеств, установления соответствия между их элементами. В среднем и старшем дошкольном возрасте целесообразно обучать различным операциям с множествами, учить сравнивать множества, обладающие разными качественными признаками, видеть равенство и неравенство множеств как практически (вне счета), так и обучая счету с помощью слов-числительных. § 3. Роль различных анализаторов в развитии навыков счета и представлений о множестве Ребенок окружен различными множествами, выраженными не только предметами, но и звуками, движениями и т. д. Эти множества ребенок воспринимает различными анализаторами: зрительным, слуховым, осязательным, кинестетическим и др. Через интерорецепцию ощущений ребенок воспринимает двигательные акты сердца, дыхания и др. Все эти ощущения, передаваемые в кору головного мозга, служат основой формирования представления о неопределенной множественности разных явлений, что и подчеркивал в своих высказываниях И. М. Сеченов. Повторяющиеся однородные предметы и явления ребенок начинает сопровождать одинаково повторяющимся словом: «Вот... вот... вот...» и др. На разных этапах восприятия множества и его элементов анализаторы играют различную роль. Кинестетический анализатор играет ведущую роль в формировании как самой деятельности счета, так и представлений о множественности и множестве. Счет вне движения невозможен. Например, мы считаем находящихся в аудитории студентов, казалось бы, молча, не прибегая к движению рук, но мы считаем глазами, перенося свой взор с одного человека на другого. Кроме того, мы мысленно произносим слова-числительные. Этих слов никто не слышит, однако физиологические исследования при помощи специальной аппаратуры свидетельствуют о движении нашего речедвигательного аппарата. То же самое происходит и при восприятии множества другими анализаторами. Считая звуки, мы нередко не только мысленно называем числительные, но и слегка киваем головой или делаем другие ритмические движения (рукой, ногой), как бы отделяя каждый звук, и благодаря этому воспринимаем его более отчетливо. Не случайно И. М. Сеченов назвал двигательный анализатор дробным анализатором времени и пространства. Таким образом, счет вне участия в той или иной форме двигательного анализатора невозможен. И чем в меньшей степени развита у детей деятельность счета, тем большую роль в ней играет движение. Так, на самых ранних этапах развития счетной деятельности ребенок, сравнивая множества, действенно сопоставляет элементы одного множества с элементами другого один к одному, так как устанавливает между ними взаимно-однозначное соответствие. Овладевая счетом с помощью слов-числительных, он громко произносит их, показывая на предметы и действенно соотнося каждое из них с одним из элементов множества. И даже тогда, когда взрослые, считая глазами, молча, встречаются с теми или иными затруднениями, они неизбежно прибегают к движениям руки (например, при подсчете голосов в большой аудитории). Показывающая рука счетчика помогает более четко сосчитать поднятые руки голосующих. Не случайно и то, что почти во всех языках первые слова-числительные состоят из односложных слов. В нашем русском языке числительное один нередко заменяется односложным словом раз. Слова-числительные раз, два, три, четыре, пять, шесть, семь и т. д. позволяют отметить ритм движения. Поэтому они широко используются там, где требуется четко воспроизвести ритм,— на физкультурных занятиях, при обучении музыке, пению, танцам, в ритмической гимнастике и т. д. Народная педагогика подметила связь первых слов-числительных с движением и создала так называемые считалочки. Все это дает основание считать двигательный анализатор ведущим в отсчитывании элементов множеств и в формировании первых представлений о множестве. Различную роль на разных этапах развития играют и другие анализаторы. Рассмотрим роль зрительного анализатора, В раннем детстве, когда внимание ребенка привлечено к границам множества, когда в первую очередь фиксируются именно они значительно усиливается роль зрительного анализатора. Дети зрительно воспринимают множество как единое пространственно-замкнутое целое. В дальнейшем все в большей и в большей степени развивается взаимодействие двух анализаторов: зрительного и двигательного, чему в значительной мере способствует правильное педагогическое руководство. Приемы наложения и приложения ставят детей перед необходимостью воспринять не только множество в его границах, но и зрительно следить за каждым элементом множества и воспроизводить его; это перестраивает, как уже говорилось выше, характер движения рук детей (см. стр. 60). Зрительное восприятие целого в единстве с его элементами становится все более совершенным. Линейное расположение элементов множеств помогает развитию у детей умений отмечать рукою и следить глазами за последовательностью всех элементов множества слева направо. Это, в свою очередь, формирует стереотип в движениях глаз и руки, прослеживающих каждый из предметов совокупности, и готовит детей к счетной операции с помощью слов-числительных. При дочисловом сравнении множеств путем сопоставления элементов множеств один к одному ребенок подводится через движение к зрительному восприятию. Сравнивая обе совокупности, он видит равенство и неравенство их. Таким образом, действенно и зрительно воспринимая множество в его единстве с элементами, ребенок начинает различать множества по их мощности и отражать это в слове. Постепенно у детей формируется потребность не только различать, но и считать количество элементов с помощью слов-числительных: речедвигательный анализатор вступает в связь с движением руки и глаз и со зрительным восприятием совокупности. В условиях правильно организованной педагогической работы эти связи развиваются. Все это еще раз подтверждает вывод о том, что не с обучения счету с помощью слов-числительных следует начинать обучение маленьких детей, а с действенного создания множеств самими детьми и сравнения их приемами наложения и приложения, что постепенно знакомит детей с равенством и неравенством совокупностей («Грибков на верхней полоске больше, а кружков на нижней меньше, или: зайчиков больше, а морковок меньше, или: кукол и чашек поровну, чашек столько, сколько кукол», и т. д.). Наиболее отчетливому зрительному восприятию множества как целого и его элементов способствует линейное расположение множества. Какую же роль играет называние детьми числительных, в котором участвует речедвигательный анализатор? Дети очень рано склонны повторять за взрослыми слова-числительные. Чем же это вызвано и какую функцию они выполняют? Саша (2 года 3 мес.), наблюдая за огнями в домах города, двигает рукою, как бы показывая на них, и сопровождает словами: раз, три, пять, восемь, т. е. подражает движениям взрослых при счете. Дети четырех-пяти лет, раскачиваясь на качалке, сопровождают свои движения называнием числительных: раз, два, три, четыре, пять, шесть, семь, восемь, четырнадцать, а затем после остановки повторяют те же слова. Слова-числительные ритмизируют движения. Вполне справедливо отметила Н. А. Менчинская, что первые слова-числительные служат своеобразным аккомпанементом общим движениям детей. Дети относительно легко запоминают и порядок слов-числительных, если взрослые обучают их этому. Однако и при хаотическом назывании числительных, и при назывании по порядку у детей образуются чисто слухо-речедви-гательные связи, которые постепенно вступают в связь с общими движениями рук, туловища, головы и др. Произносимые слова-числительные ритмизируют общие движения подобно тому, как у взрослых в физкультурных упражнениях, в строю они регулируют ритм. Произносимые слова-числительные не означают деятельности счета и не служат обобщению количества. И если такая односторонняя связь многократно повторяется, то она постепенно приобретает для ребенка особый смысл, а именно служит своеобразным сигналом к остановке, типа слова стоп. Ребенок, который, казалось бы, научился считать, при воспроизведении множества по заданному числу, перебирая предметы и называя числительные, ждет, когда в его речи появится заданное ему слово-числительное. И если он пропускает его, то продолжает дальше называть все известные ему числительные, раскладывая предметы. Такая сигнальная функция числительных наблюдается у детей пяти-шести-семи лет, особенно это ярко выражено у детей пятилетнего возраста. Так, многие дети пяти лет, отсчитывая пуговицы по указанному числу, сопровождают отбор пуговиц называнием числительных. Однако это не счет для определения количества. Называя числительные, дети ожидают, когда появится указанное им слово-числительное, после чего прекращают дальнейший отбор. Ответить же на вопрос, сколько пуговиц они отобрали, дети не могут даже в том случае, когда они их снова пересчитывали, показывая пальцем. Итоговое число для них не служит показателем мощности множества, а является лишь условным сигналом к остановке, как то и было показано на поведении Юры П. (см. стр. 66—67). Итак, в результате заучивания слов-числительных складывается лишь речедвигательный стереотип, а отдельные числительные выполняют функцию сигнала к остановке. Отсюда вытекает вывод: слова-числительные, даже произносимые по порядку, являются не чем иным, как речедвигательным стереотипом, а не пониманием значения числа. Поэтому раннее обучение называнию слов-числительных, хотя бы и по порядку, отнюдь не содействует развитию деятельности счета и пониманию значения числа. Какова же роль слухового анализатора в обучении детей деятельности счета и в формировании понятия числа? Выше уже указывалось, что повторяемость однородных движений создает представление о множестве в границах времени. То же самое происходит и при восприятии звуков, воспринимаемых на слух, т. е. во временной последовательности. Восприятие звуков и движений одного за другим способствует более четкому дифференцированию элементов множества, которые синтезируются в уме в единое целое в границах времени (начало и конец). Маленьким детям, не знающим счета и слов-числительных, воспитатель предлагает постучать столько же раз, сколько раз стучал педагог. Ребенок слышал звуки и видел движения его руки. Как же он воспринимает и воспроизводит их? На втором году жизни дети еще не воспроизводят воспринятое ими количество на слух: вместо двух-трех предъявленных им звуков стучат много раз. Несколько позднее, по мере упражнений, они начинают вслушиваться в количество звуков, всматриваться в количество производимых воспитателем движений и три — пять звуков начинают отстукивать правильно. Значит, и в данном случае восприятие множества на слух развивается от неопределенной множественности к множеству, когда последовательно воспринимаемые звуки в небольшом количестве трех— пяти начинают синтезироваться в границах времени, восприниматься детьми как структурно-замкнутое целое. Такая , перестройка, как показывает исследование, происходит в те же периоды жизни, как и зрительное восприятие множества. Но если воспринимаемые ребенком звуки сопровождать называнием числительных или даже бессмысленными словами считалочки, ребенок воспроизводит их в большем, чем обычно, количестве. Слово, сопровождающее звук, способствует более четкому дифференцированию каждого звука-движения. Отсюда следует вывод, что ритмическое называние слов считалочки или слов-числительных помогает более четко дифференцировать отдельные элементы множества, воспринимаемые на слух и воспроизводимые в движении, подобно тому как произносимое ребенком в раннем возрасте слово еще, еще... еще... или вот... вот... помогало ему дифференцировать элементы предметного множества. И если зрительный анализатор способствует синтезированию отдельных элементов в единое структурно-замкнутое целое, то слуховой, двигательный и речедвигательный анализаторы способствуют вычленению отдельных элементов внутри этого целого. Такое взаимодействие анализаторов является весьма важным для развития восприятия множества в целом и образующих его элементов. Отсюда следует педагогический вывод о необходимости использовать при формировании у детей счетной деятельности и представления о множестве все анализаторы. Между множествами, воспринимаемыми разными анализаторами, устанавливается взаимно-однозначное соответствие. |
