Лекция погрешности
 Скачать 126.51 Kb. Скачать 126.51 Kb.
|
|
ЛЕКЦИЯ – ПОГРЕШНОСТИ Методы обработки результатов физического эксперимента 1. Измерение. Классификация измерений Измерение – это нахождение значения физической величины опытным путем с помощью специальных технических средств и выражение полученного результата в принятых единицах. Прямым называется измерение, при котором значение измеряемой величины непосредственно считывается со шкалы прибора, проградуированного в соответствующих единицах измерения. Уравнение прямого измерения имеет вид у = сx, где у – значение измеряемой величины; с – цена деления шкалы прибора в единицах измеряемой величины; x – отсчет по индикаторному устройству в делениях шкалы. Примерами прямых измерений являются: измерение длины предмета с помощью штангенциркуля или микрометра, измерение силы тока амперметром, напряжения – вольтметром, температуры – термометром и др. Косвенным называется измерение, результат которого определяют на основании прямых измерений величин, связанных с измеряемой величиной известной зависимостью. Уравнение косвенного измерения имеет вид у = f(x1, x2, …, xn), где у – искомая величина, являющаяся функцией величин x1, x2, …, xn, измеряемых прямым методом. Можно сказать, что косвенное измерение – это измерение, результат которого рассчитывается по формуле. Примерами косвенных измерений являются: определение радиуса шара R = D/2, площади его поверхности S = D 2 или объёма V = D 3 /6 по прямо измеренной величине – диаметру шара D. Совместными называют производимые одновременно измерения двух или нескольких неодноименных величин для нахождения зависимости между ними. Уравнение совместных измерений имеет вид yi = f (x1i , x2i , …, xni ; a, b, c, ...), i = 1, 2, ..., N, где yi , x1i , x2i , ..., xni – значения величин, измеренных одновременно (прямо или косвенно) в i-й измерительной операции; а, b, с, ... – неизвестные искомые величины. Для решения полученной системы используют метод наименьших квадратов. Примером совместных измерений может служить нахождение зависимости периода Т колебаний математического маятника от его длины l: Т = al n , где а и n – неизвестные параметры, определяемые методом наименьших квадратов по прямым измерениям l и Т. Совокупными называют такие одновременно проводимые измерения нескольких одноименных величин, при которых значения искомых величин находят решением системы уравнений, получаемых при измерениях различных сочетаний этих величин. Пример совокупных измерений – нахождение ёмкости двух конденсаторов по результатам измерений ёмкости каждого из них в отдельности, а также при последовательном и параллельном соединениях. Каждое из этих измерений выполняется с одним наблюдением, но в итоге для двух неизвестных будем иметь четыре уравнения: С1 = x1, С2 = x2 , С1+С2 = x3, C1C2/(C1 + С2) = x4. 2. Классификация погрешностей измерения Целью любого измерения является нахождение истинного значения физической величины. Но при измерении любой физической величины принципиально невозможно определить это истинное значение. Разность между результатом измерения и истинным значением называется истинной погрешностью измерения. В силу того, что истинное значение неизвестно, неизвестной является и истинная погрешность. Учитывая, что ни истинное значение физической величины, ни истинную погрешность в опыте определить невозможно, задачу нахождения истинного значения формулируют как задачу нахождения некоторого приближенного к нему значения с указанием диапазона возможных отклонений этого приближенного значения от истинного значения. Найденное в эксперименте приближенное значение измеряемой величины, называется оценкой физической величины. Оценка с указанием ее возможного интервала отклонения от истинного значения называется результатом измерения. Погрешность измерения включает в себя множество различных составляющих, которые можно классифицировать по различным признакам. В настоящее время классификация погрешностей содержит около 30 видов. Основные виды погрешностей. 1) Систематическая погрешность – это составляющая погрешности измерения, которая остаётся постоянной или закономерно изменяется при повторных измерениях (смещение нуля прибора, неточность градуировки шкалы прибора и т.д.). Обнаруженные систематические погрешности исключаются из результатов измерений. 2) Случайная погрешность – это вид погрешности, изменяющейся случайным образом при повторных измерениях. Ее наличие обусловлено влиянием большого числа случайных факторов, воздействие которых на каждое отдельное измерение невозможно учесть или заранее предсказать. Оценка случайной погрешности производится методами математической статистики. 3) Грубая погрешность – погрешность измерения, значительно превышающая погрешности большинства результатов наблюдений. Такие погрешности могут возникать вследствие резкого изменения внешних условий эксперимента: внезапного изменения температуры, напряжения в сети и т. п. Грубые погрешности обнаруживают статистическими методами и соответствующие результаты измерений исключают из рассмотрения. 4) Промах – это вид грубой погрешности, зависящий от наблюдателя и связанный с неправильным обращением со средствами измерений: неверными отсчетами показаний приборов, описками при записи результатов, невнимательностью экспериментатора, путаницей номеров образцов и т. п. Результаты наблюдений, содержащие промахи, как заведомо неправильные, исключают из рассмотрения. 5) Приборная погрешность Qx – погрешность применяемых измерительных средств. В случае аналогового прибора приборная погрешность вычисляется как половина минимального деления шкалы прибора. В случае цифрового прибора приборной погрешностью является минимальное деление шкалы. Класс точности прибора γ – характеристика прибора, выраженная его основной и дополнительной погрешностей, означает максимальную относительную погрешность измерения в процентах. Класс точности указывается на шкале прибора. Приборная погрешность вычисляется через класс точности как 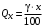 , где x – минимальное деление шкалы. , где x – минимальное деление шкалы.Полная погрешность измерения, являющаяся суммой указанных погрешностей, может быть представлена в абсолютном и относительном виде. Абсолютная погрешность 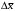 – это погрешность измерения, выраженная в единицах измеряемой величины. – это погрешность измерения, выраженная в единицах измеряемой величины. Относительная погрешность δx – это погрешность измерения, выраженная отношением абсолютной погрешности к результату измерения. Измеряется в процентах. случайной доверительной погрешностью результата измерения. полной погрешностью результата измерения. 3. Округление результата измерения При округлении используют следующие правила (ГОСТ Р 8.736-2011): 1) Предварительно результат и погрешность записывают в нормализованном экспоненциальном виде: общий показатель степени выносят за скобку или заменяют соответствующей приставкой: микро, милли, кило, мега и др. Например, x = 0.022 ± 0.003 м = (2.2 ± 0.3)·10-3 м = 2.2 ± 0.3 см. Запрещены записи вида x = 22·10-3 ± 30·10-4 м или x = 0.022 ± 3·10-3 м. Показатель 101 не выносится. 2) Если результат будет в дальнейшем использован в вычислениях, то во избежание накопления погрешностей за счет округлений погрешность округляют до двух значащих цифр при любой первой. При промежуточных вычислениях величин  и и  следует сохранять не менее четырех значащих цифр. следует сохранять не менее четырех значащих цифр. 3) Если результат измерения является окончательным и не будет использован в вычислениях других величин, то доверительную погрешность x округляют до первой значащей цифры, если она больше 3, или до двух значащих цифр, если первая равна 1, 2 или 3. 4) Среднее значение 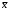 округляют до того разряда, которым оканчивается округленная погрешность округляют до того разряда, которым оканчивается округленная погрешность 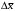 . .
Если погрешность округляется до двух значащих цифр, но вторая из них равна нулю, то этот нуль сохраняется, а в соответствующем ему разряде результата записывается получающаяся там значащая цифра: x = 3.48 ± 0.10. Алгоритм расчета погрешности прямых измерений Пусть дана последовательность (выборка) значений прямо измеренной величины х:
N = 5; Р = 95% - доверительная вероятность (применяется алгоритм, разработанный для 95% всех значений). 1) Из результатов измерений исключить известные систематические погрешности. 2) Упорядочить выборку в порядке возрастания (ранжировать выборку):
3) Провести проверку на промахи по размаху выборки. R – размах выборки; 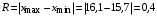 ; ;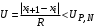 ; ; 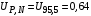 - статистический коэффициент; - статистический коэффициент;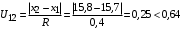 => х1 = 15,7 – не промах; => х1 = 15,7 – не промах;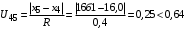 => х5 = 16,1 – не промах; => х5 = 16,1 – не промах;Промахов нет. (Если 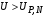 , то хi (крайнее) – промах, исключается из выборки). , то хi (крайнее) – промах, исключается из выборки).4) Повторить проверку на промахи по п.3 с новыми R и N до тех пор, пока не будут исключены все промахи. 5) Рассчитать выборочное среднее: 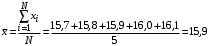 . .6) Вычислить среднеквадратичное отклонение среднего (СКО) (основа случайной погрешности, формула разработана в рамках математической статистики): 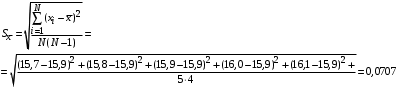 7.1) Рассчитать случайную погрешность по Стъюденту: 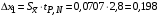 ; ; 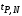 - коэффициент Стъюдента; для N = 5 - коэффициент Стъюдента; для N = 5 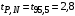 . .7.2) Рассчитать случайную погрешность по размаху выборки: 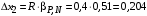 ; ; 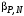 - статистический коэффициент; для N = 5 - статистический коэффициент; для N = 5 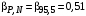 . .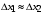 . .8) Определить приборную погрешность: Qх = 0,2. 9) Рассчитать полную погрешность результата измерений: 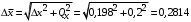 . .10) Рассчитать относительную погрешность: 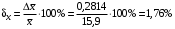 . .11) Записать окончательный результат и округлить: 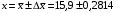 ; ;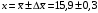 ; ; 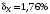 ; Р = 95%. ; Р = 95%.Алгоритм расчета погрешности косвенных измерений методом переноса погрешностей Метод используется в случае, когда значения прямо измеренных величин образуют выборку. Пусть даны результаты прямых измерений величин x и y:
Косвенно измеренная величина связана с прямо измеренными формулой: 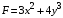 1) По алгоритму расчета погрешности прямых измерений рассчитать величины 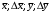 : :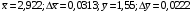 . .2) Рассчитать среднее значение функции: 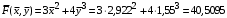 . .3.1) Рассчитать в точке ( 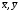 ) частные производные от функции: ) частные производные от функции: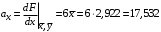 , ,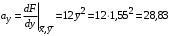 . .3.2) Если функция легко логарифмируется, то рассчитать частные производные от ее логарифма: 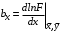 , , 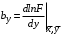 . .4.1) По формуле переноса погрешностей вычислить полную погрешность функции: 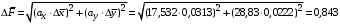 . .4.2) Для логарифмируемой функции формула полной погрешности: 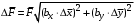 . .5) Рассчитать относительную погрешность: 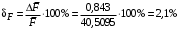 . .6) Записать окончательный результат и округлить: 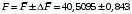 ; ;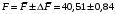 ; ; 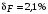 ; Р = 95%. ; Р = 95%.Алгоритм расчета погрешности косвенных измерений методом выборок Метод используется в случае, когда значения прямо измеренных величин, определяемые из различных опытов, могут существенно отличаться друг от друга. Пусть даны результаты прямых измерений величин x и y:
Косвенно измеренная величина связана с прямо измеренными формулой: 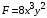 . .1) Рассчитать значения функции Fi (xi, yi) по каждому набору прямых измерений: F1(x1, y1) = 8·0,103·25,552 = 5,222; F2(x2, y2) = 8·0,203·9,042 = 5,23; F3(x3, y3) = 8·0,303·4,912 = 5,207; F4(x4, y4) = 8·0,403·3,192 = 5,21; F5(x5, y5) = 8·0,503·2,2952 = 5,244. 2) Обработать полученную выборку Fi по алгоритму прямых измерений; найти среднее значение 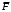 и случайную погрешность и случайную погрешность 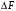 (без приборной!): (без приборной!):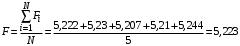 ; ;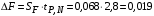 . .3.1) Вывести выражения для частных производных от функции: 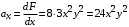 , ,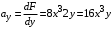 . .3.2) Вывести для легко логарифмируемой функции выражения для частных производных от ее логарифма: 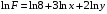 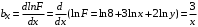 , ,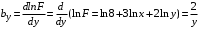 . .4.1) Рассчитать приборную погрешность функции для случая различных приборных погрешностей прямо измеренных величин по формуле: 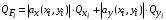 ; ;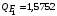 ; ; 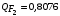 ; ; 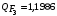 ; ; 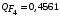 ; ; 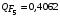 . .Вычислить среднюю приборную погрешность функции: 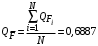 . .4.2) Если приборные погрешности прямо измеренных величин не меняются, то приборную погрешность функции можно рассчитать по формуле: 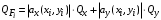 ; ;или 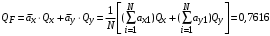 . .5) Вычислить полную погрешность функции: 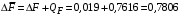 . .6) Рассчитать относительную погрешность: 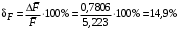 . .6) Записать окончательный результат и округлить: 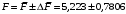 ; ;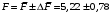 ; ; 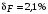 ; Р = 95%. ; Р = 95%. |
