21.02.2022 Лекция. Лекция Поток вектора напряженности. Теорема Гаусса Остроградского
 Скачать 119.47 Kb. Скачать 119.47 Kb.
|
|
Лекция 2. Поток вектора напряженности. Теорема Гаусса — Остроградского 2.1. Поток вектора напряжения Чтобы продвинуться дальше в изучении электрического поля, необходимо использовать векторный анализ — математический аппарат. Мы должны знать, что такое градиент, ротор, дивиргенция. Начнем же с понятия “поток вектора 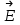 “. “.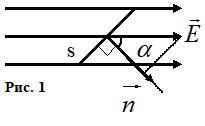 Пусть имеем однородное электрическое поле (напряженность которого одинакова во всех точках пространства) с напряженностью 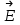 , которое пронизывает некоторую плоскую поверхность площади S, тогда скалярное произведение , которое пронизывает некоторую плоскую поверхность площади S, тогда скалярное произведение 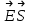 будет называться потоком вектора напряженности будет называться потоком вектора напряженности 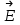 через поверхность S, (см. рис. 1), т.е. через поверхность S, (см. рис. 1), т.е.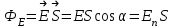 , (1) , (1)где 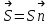 — есть вектор, равный произведению величины площади на нормаль к этой поверхности, Еn –проекция вектора — есть вектор, равный произведению величины площади на нормаль к этой поверхности, Еn –проекция вектора 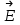 на нормаль на нормаль 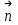 к площадке. к площадке.В общем случае поле может быть неоднородным, поверхность неплоской. В этом случае поверхность можно мысленно разбить на бесконечно малые элементарные площадки dS, которые можно считать плоскими, а поле вблизи них однородным. В таком случае поток через элементарную площадку 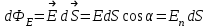 . (2) . (2)Полный поток вектора напряженности через поверхность S 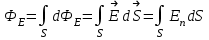 . (3) . (3)2.2. Теорема Гаусса-Остроградского 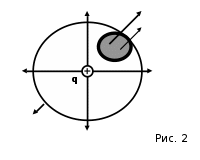 Найдем поток вектора напряженности электрического поля, создаваемого точечным зарядом q, через сферическую поверхность радиуса r. Площадь ее поверхности 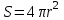 . Силовые линии электрического поля, (см. рис. 2), идут по радиусам к поверхности сферы и поэтому угол между векторами . Силовые линии электрического поля, (см. рис. 2), идут по радиусам к поверхности сферы и поэтому угол между векторами 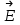 и и 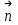 равен нулю. равен нулю.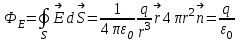 . (4) . (4)Можно показать, что поток через замкнутую поверхность не зависит от формы поверхности и от расположения зарядов в ней. Рассмотрим поток, создаваемый системой зарядов, сквозь замкнутую поверхность произвольной формы, внутри которой они находятся (рис.3): 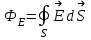 . .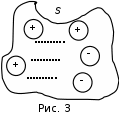 Согласно принципу суперпозиции 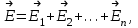 поэтому поэтому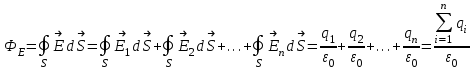 таким образом таким образом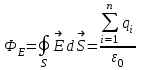 . (5) . (5)Итак, мы доказали теорему Гаусса - Остроградского: «полный поток вектора напряженности электростатического поля через произвольную замкнутую поверхность равен алгебраической сумме зарядов, охватываемых этой поверхностью, деленной на 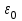 ». ».Теорему Гаусса — Остроградского, (5), можно записать в дифференциальной форме: 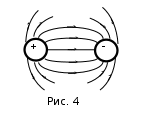 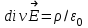 , (6) , (6)где 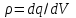 - объемная плотность заряда. - объемная плотность заряда.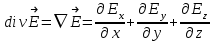 , знак , знак 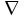 - оператор набла. - оператор набла.Из теоремы Гаусса — Остроградского вытекают следствия: 1) линии вектора 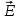 (силовые линии) нигде, кроме зарядов, не начинаются и не заканчиваются: они, начавшись на заряде, уходят в бесконечность для положительного заряда, либо, приходя из бесконечности, заканчиваются на отрицательном заряде (картина силовых линий приводится на рис. 4); (силовые линии) нигде, кроме зарядов, не начинаются и не заканчиваются: они, начавшись на заряде, уходят в бесконечность для положительного заряда, либо, приходя из бесконечности, заканчиваются на отрицательном заряде (картина силовых линий приводится на рис. 4);2) если алгебраическая сумма зарядов, охватываемых замкнутой поверхностью, равна нулю, то полный поток через эту поверхность равен нулю; 3) если замкнутая поверхность проведена в поле так, что внутри нее нет зарядов, то число входящих линий вектора напряженности равно числу выходящих и поэтому полный поток через такую поверхность равен нулю. |
