курс. Курс лекций по ТАУ. Лекция Принципы управления 2 Общие понятия 2 Лекция Статический режим сау 7

• Название: Лекция Принципы управления 2 Общие понятия 2 Лекция Статический режим сау 7
• Дата: 06.12.2021
• Размер: 1.6 Mb.
• Имя файла: Курс лекций по ТАУ.doc
• Тип: Лекция; #293385
• страница: 4 из 22

3.3. Передаточная функция

 

В ТАУ часто используют операторную форму записи дифференциальных уравнений. При этом вводится понятие дифференциального оператора p = d/dt так, что, dy/dt = py, а pⁿ = dⁿ/dtⁿ. Это лишь другое обозначение операции дифференцирования. Обратная дифференцированию операция интегрирования записывается как 1/p. В операторной форме исходное дифференциальное уравнение записывается как алгебраическое:

 

a_op⁽ⁿ⁾y + a₁p^(n-1)y + ... + a_ny = (a_op⁽ⁿ⁾ + a₁p^(n-1) + ... + a_n)y = (b_op^(m) + b₁p^(m-1) + ... + bm)u

Не надо путать эту форму записи с операционным исчислением хотя бы потому, что здесь используются непосредственно функции времени y(t), u(t) (оригиналы), а не их изображения Y(p), U(p), получаемые из оригиналов по формуле преобразования Лапласа. Вместе с тем при нулевых начальных условиях с точностью до обозначений записи действительно очень похожи. Это сходство лежит в природе дифференциальных уравнений. Поэтому некоторые правила операционного исчисления применимы к операторной форме записи уравнения динамики. Так оператор p можно рассматривать в качестве сомножителя без права перестановки, то есть py yp. Его можно выносить за скобки и т.п.

Поэтому уравнение динамики можно записать также в виде: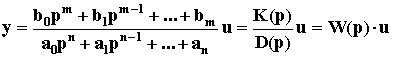

 



 

Дифференциальный оператор W(p) называют передаточной функцией. Она определяет отношение выходной величины звена к входной в каждый момент времени: W(p) = y(t)/u(t), поэтому ее еще называют динамическим коэффициентом усиления. В установившемся режиме d/dt = 0, то есть p = 0, поэтому передаточная функция превращается в коэффициент передачи звена K = b_m/a_n.

Знаменатель передаточной функции D(p) = a_opⁿ + a₁p^{n - 1} + a₂p^{n - 2} + ... + a_n называют характеристическим полиномом. Его корни, то есть значения p, при которых знаменатель D(p) обращается в ноль, а W(p) стремится к бесконечности, называются полюсами передаточной функции.

Числитель K(p) = b_op^m + b₁p^{m - 1}+ ... + b_m называют операторным коэффициентом передачи. Его корни, при которых K(p) = 0 и W(p) = 0, называются нулями передаточной функции.

Звено САУ с известной передаточной функцией называется динамическим звеном. Оно изображается прямоугольником, внутри которого записывается выражение передаточной функции. То есть это обычное функциональное звено, функция которого задана математической зависимостью выходной величины от входной в динамическом режиме. Для звена с двумя входами и одним выходом должны быть записаны две передаточные функции по каждому из входов. Передаточная функция является основной характеристикой звена в динамическом режиме, из которой можно получить все остальные характеристики. Она определяется только параметрами системы и не зависит от входных и выходных величин. Например, одним из динамических звеньев является интегратор. Его передаточная функция W_и(p) = 1/p. Схема САУ, составленная из динамических звеньев, называется структурной.

 

3.4. Элементарные динамические звенья

Динамика большинства функциональных элементов САУ независимо от исполнения может быть описана одинаковыми по форме дифференциальными уравнениями не более второго порядка. Такие элементы называют элементарными динамическими звеньями. Передаточная функция элементарного звена в общем виде задается отношением двух полиномов не более чем второй степени:

 

W_э(p) = .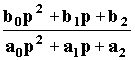

 

Известно также, что любой полином произвольного порядка можно разложить на простые сомножители не более, чем второго порядка. Так по теореме Виета модно записать

 

D(p) = a_opⁿ + a₁p^{n - 1} + a₂p^{n - 2} + ... + a_n = a_o(p - p₁)(p - p₂)...(p - p_n),

 

где p₁, p2, ..., p_n - корни полинома D(p). Аналогично

 

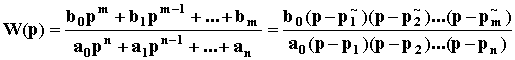
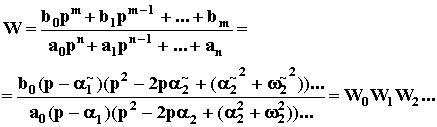
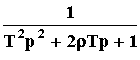K(p) = b_opm + b₁p^{m - 1}+ ... + bm = b_o(p - p₁)(p - p₂)...(p - pm),

 

где p₁, p₂, ..., pm - корни полинома K(p). То есть

 



 

Корни любого полинома могут быть либо вещественными p_i = a_i , либо комплексными попарно сопряженными p_i = a_i ± j _i . Любому вещественному корню при разложении полинома соответствует сомножитель (p - a_i ). Любая пара комплексно сопряженных корней соответствует полиному второй степени, так как

 

(p - a_i + j _i )(p - a_i - j _i ) = (p - ai)² + _i ² = p² - 2pa_i + (a_i ² + _i ²).

 

То есть



 

Поэтому любую сложную передаточную функцию линеаризованной САУ можно представить как произведение передаточных функций элементарных звеньев. Каждому такому звену в реальной САУ, как правило, соответствует какой - то отдельный узел. Зная свойства отдельных звеньев можно судить о динамики САУ в целом.

В теории удобно ограничиться рассмотрением типовых звеньев, передаточные функции которых имеют числитель или знаменатель, равный единице, то есть

W(p) = , W(p) = ,

W(p) = 1/p, W(p) = p, W(p) = Tp + 1, W(p) = k.

Из них могут быть образованы все остальные звенья. Звенья, у которых порядок полинома числителя больше порядка полинома знаменателя, технически нереализуемы.