|
|
курс. Курс лекций по ТАУ. Лекция Принципы управления 2 Общие понятия 2 Лекция Статический режим сау 7
3.1. Динамический режим САУ.
Уравнение динамики
Установившийся режим не является характерным для САУ. Обычно на управляемый процесс действуют различные возмущения, отклоняющие управляемый параметр от заданной величины.
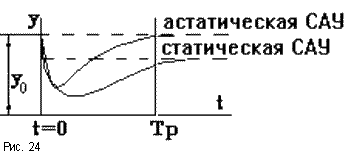
Процесс установления требуемого значения управляемой величины называется регулированием. Ввиду инерционности звеньев регулирование не может осуществляться мгновенно.
Рассмотрим САР, находящуюся в установившемся режиме, характеризующемся значением выходной величины y = yo. Пусть в момент t = 0 на объект воздействовал какой - либо возмущающий фактор, отклонив значение регулируемой величины. Через некоторое время регулятор вернет САР к первоначальному состоянию (с учетом статической точности) (рис.24). Если регулируемая величина изменяется во времени по апериодическому закону, то процесс регулирования называется апериодическим.
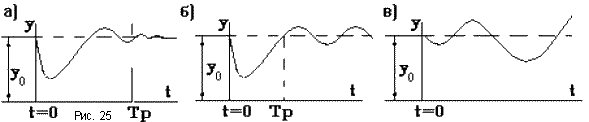
При резких возмущениях возможен колебательный затухающий процесс (рис.25а). Существует и такая вероятность, что после некоторого времени Тр в системе установятся незатухающие колебания регулируемой величины - незатухающий колебательный процесс (рис.25б). Последний вид - расходящийся колебательный процесс (рис.25в).
Таким образом, основным режимом работы САУ считается динамический режим, характеризующийся протеканием в ней переходных процессов. Поэтому второй основной задачей при разработке САУ является анализ динамических режимов работы САУ.
Поведение САУ или любого ее звена в динамических режимах описывается уравнением динамики y(t) = F(u,f,t), описывающее изменение величин во времени. Как правило, это дифференциальное уравнение или система дифференциальных уравнений. Поэтому основным методом исследования САУ в динамических режимах является метод решения дифференциальных уравнений. Порядок дифференциальных уравнений может быть довольно высоким, то есть зависимостью связаны как сами входные и выходные величины u(t), f(t), y(t), так и скорости их изменения, ускорения и т.д. Поэтому уравнение динамики в общем виде можно записать так:
F(y, y’, y”,..., y(n), u, u’, u”,..., u(m), f, f ’, f ”,..., f(k)) = 0.
3.2. Линеаризация уравнения динамики
В общем случае уравнение динамики оказывается нелинейным, так как реальные звенья САУ обычно нелинейны. В целях упрощения теории нелинейные уравнения заменяют линейными, которые приблизительно описывают динамические процессы в САУ. Получаемая при этом точность уравнений оказывается достаточной для технических задач. Процесс преобразования нелинейных уравнений в линейные называется линеаризацией уравнений динамики. Рассмотрим сначала геометрическое обоснование линеаризации.
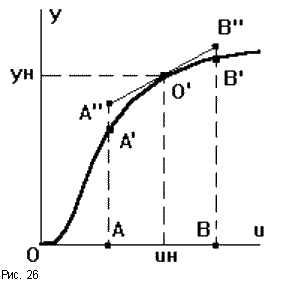
В нормально функционирующей САУ значение регулируемой и всех промежуточных величин незначительно отличается от требуемых. В пределах малых отклонений все нелинейные зависимости между величинами, входящими уравнение динамики, могут быть приближенно представлены отрезками прямых линий. Например, нелинейная статическая характеристика звена на участке АВ (рис.26) может быть представлена отрезком касательной в точке номинального режима А"В". Начало координат переносится в точку О’, и в уравнениях записываются не абсолютные значения величин y,u,f, а их отклонения от номинальных значений: y = y - yн, u = u - uн, f = f - fн. Это позволяет получить нулевые начальные условия, если считать, что при t 0 система находилась в номинальном режиме в состоянии покоя.
Математическое обоснование линеаризации состоит в том, что если известно значение f(a) какой - либо функции f(x) в любой точке x = a, а также значения производных от этой функции в данной точке f’(a), f”(a), ..., f(n)(a), то в любой другой достаточно близкой точке x + x значение функции можно определить, разложив ее в окрестности точки a в ряд Тейлора:
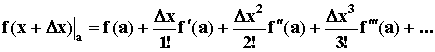
Аналогично можно разложить и функцию нескольких переменных. Для простоты возьмем упрощенный, но наиболее характерный вариант уравнения динамики САУ: F(y,y',y",u,u') = f. Здесь производные по времени u',y',y" также являются переменными. В точке, близкой к номинальному режиму: f = fн + f и F = Fн + F. Разложим функцию F в ряд Тейлора в окрестности точки номинального режима, отбрасывая члены ряда высоких порядков малости:
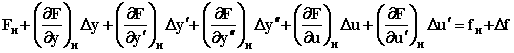 . .
В номинальном режиме, когда все отклонения и их производные по времени равны нулю, получаем частное решение уравнения: Fн = fн. Учитывая это и вводя обозначения получим:
ao y” + a1 y’ + a2 y = bo u’ + b1 u + co f.
Отбрасывая все знаки , получим:
aoy” + a1y’ + a2y = bou’ + b1u + cof.
Отбрасывая все знаки , получим:
В более общем случае:
aoy(n) + a1y(n-1) + ... + an - 1y’ + any = bou(m) + ... + bm - 1u’ + bmu + cof.
При этом всегда нужно помнить, что в данном уравнении используются не абсолютные значения величин y, u, f их производных по времени, а отклонения этих величин от номинальных значений. Поэтому полученное уравнение будем называть уравнением в отклонениях.
К линеаризованной САУ можно применить принцип суперпозиции: реакция системы на несколько одновременно действующих входных воздействий равна сумме реакций на каждое воздействие в отдельности. Это позволяет звено с двумя входами u и f разложить на два звена, каждое из которых имеет один вход и один выход (рис.27). Поэтому в дальнейшем мы ограничимся изучением поведения систем и звеньев с одним входом, уравнение динамики которых имеет вид:
aoy(n) + a1y(n-1) + ... + an - 1y’ + any = bou(m) + ... + bm - 1u’ + bmu.

Это уравнение описывает САУ в динамическом режиме лишь приближенно с той точностью, которую дает линеаризация. Однако следует помнить, что линеаризация возможна только при достаточно малых отклонениях величин и при отсутствии разрывов в функции F в окрестностях интересующей нас точки, которые могут быть созданы различными выключателями, реле и т.п.
Обычно n m, так как при n < m САУ технически нереализуемы.
|
|
|
 Скачать 1.6 Mb.
Скачать 1.6 Mb.