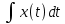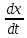Практика. Практика № 3 и 4 (15.03.22). Практическая работа 3 (2 часа) расчетное моделирование типовых звеньев систем автоматического регулирования в mathcad
 Скачать 248.91 Kb. Скачать 248.91 Kb.
|
|
Практическая работа № 3 (2 часа) РАСЧЕТНОЕ МОДЕЛИРОВАНИЕ ТИПОВЫХ ЗВЕНЬЕВ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В MATHCAD Цели работы 1. Изучение способов описания динамических свойств звеньев систем автоматического регулирования. 2. Получение дифференциальных уравнений, передаточных функций, переходных и частотных характеристик звеньев. 3. Расчетное построение переходных характеристик типовых динамических звеньев по их передаточным функциям для типовых воздействий. 1. Основные характеристики звеньев автоматических систем При изображении систем управления применяются два принципа — функциональный и структурный и, соответственно, схемы подразделяются на функциональные и структурные. Функциональной схемой называется такая схема, в которой каждому функциональному элементу системы соответствует определенное звено. Названия элементов и блоков указывают на выполняемые функции, например: чувствительный элемент, преобразующий элемент, датчик, управляющий блок, исполнительный блок, электродвигатель и т. д. Структурной схемой называется такая схема, в которой каждой математической операции преобразования сигнала соответствует определенное звено. В зависимости от полноты математического описания и от математических операций, выполняемых различными звеньями, для объектов могут быть составлены различные структурные схемы. Части структурной схемы называют звеньями, каждое из которых отображает алгоритм преобразования сигнала — математическую или логическую операцию. На структурных схемах звенья изображают прямоугольниками, внутри которых записывают соответствующие операторы преобразования сигналов. Прямоугольники соединяют линиями, отображающими информационные сигналы взаимодействия звеньев с указанием направлений этих сигналов (рис.1).  Типовые звенья: Уравнение, передаточная функция и переходные характеристики:  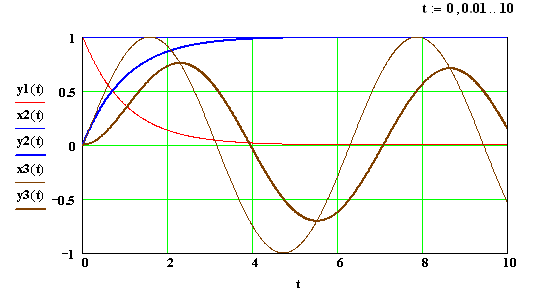 Частотные характеристики:  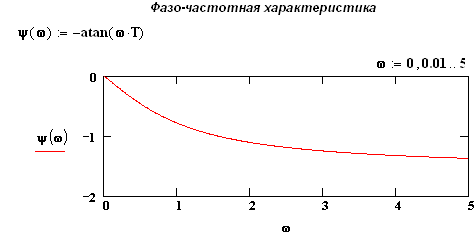 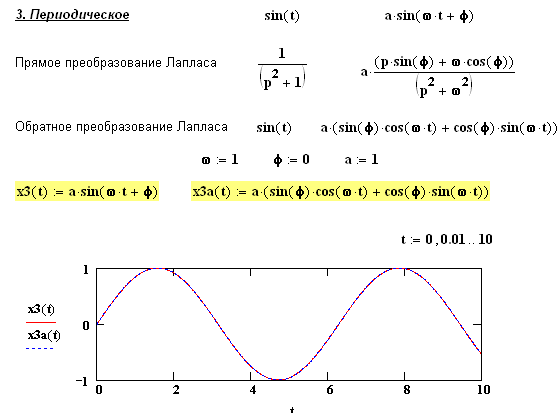 Практическая работа № 4 (2 часа) РАСЧЕТНОЕ МОДЕЛИРОВАНИЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В MATHCAD Цель работы Расчетное построение переходных характеристик САР по передаточной функции для типового воздействия методами: а) обратного преобразования Лапласа; б) решением системы обыкновенных дифференциальных уравнений (ОДУ) для разложения передаточной функции с помощью дополнительных переменных. Моделируемая САР – САР с пропорциональным (П), пропорционально-интегральным (ПИ), пропорционально-дифференциальным (ПД) и пропорционально-интегрально-дифференциальным (ПИД) регуляторами. 1. Построение передаточных функций САР. Структурная схема одноконтурной САР может быть представлена в виде, указанном на рис.1.  Рис.1. Структурная схема одноконтурной САР. G(p) – изображение задающего воздействия g(t), X(p) – изображение рассогласования x(t)=g(t)-yoc(t), F(p) – изображение возмущающего воздействия f(t), Y(p) – изображение регулируемой величины, Yoc(p) – изображение сигнала обратной связи yoc(t), W1(p) – передаточная функция исполнительного механизма, W2(p) – передаточная функция объекта регулирования, Woc(p) – передаточная функция обратной связи. Задачей САР с ПИД-регулятором является поддержание заданного значения измеряемой (регулируемой) величины. ПИД-регулятор измеряет отклонение стабилизируемой величины от заданного значения (уставки) и выдаёт управляющий сигнал, являющийся суммой трёх слагаемых, первое из которых пропорционально этому отклонению, второе пропорционально интегралу отклонения и третье пропорционально производной отклонения (или, что то же самое, производной измеряемой величины). Условное изображение ПИД-регулятора представлено на рис.2. 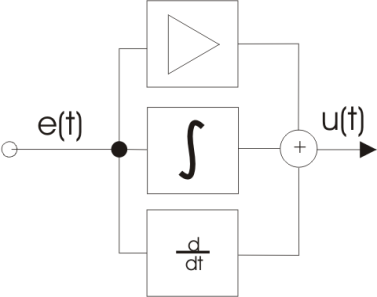 Рис.2. Схема, иллюстрирующая принцип работы ПИД-регулятора Если какие-то из составляющих не используются, то регулятор называют: пропорциональным, пропорционально-интегральным, пропорционально-дифференциальным,. Пропорциональная составляющая. Пропорциональная составляющая вырабатывает выходной сигнал, который стабилизирует отклонение регулируемой величины. Выходной сигнал пропорциональной составляющей тем больше, чем сильнее регулируемая величина отклоняется от уставки. Если входной сигнал равен уставке, то выходной равен нулю. При использовании пропорционального регулятора значение регулируемой величины никогда не стабилизируется на заданном значении. Существует так называемая статическая ошибка, которая равна такому отклонению регулируемой величины, которое обеспечивает выходной сигнал, стабилизирующий выходную величину именно на этом значении. Например, в регуляторе температуры выходной сигнал (мощность нагревателя) постепенно уменьшается при приближении температуры к уставке, и система стабилизируется при мощности равной тепловым потерям. Температура не может достичь уставки, так как в этом случае мощность нагревателя станет равна нулю, и он начнёт остывать. Чем больше коэффициент пропорциональности между входным и выходным сигналом (коэффициент усиления), тем меньше статическая ошибка, однако при слишком большом коэффициенте усиления могут начаться автоколебания, а при дальнейшем увеличении коэффициента система может потерять устойчивость. Интегральная составляющая. Для устранения статической ошибки используют интегральную составляющую. Она позволяет регулятору «учиться» на предыдущем опыте. Если система не испытывает внешних возмущений, то через некоторое время регулируемая величина стабилизируется на заданном значении, сигнал пропорциональной составляющей будет равен нулю, а выходной сигнал будет полностью обеспечивать интегральная составляющая. Дифференциальная составляющая. Дифференциальная составляющая противодействует предполагаемым отклонениям регулируемой величины, которые могут произойти в будущем. Эти отклонения могут быть вызваны внешними возмущениями или запаздыванием воздействия регулятора на систему. Чем быстрее регулируемая величина отклоняется от уставки, тем сильнее противодействие, создаваемое дифференциальной составляющей. Выходной сигнал ПИД регулятора u(t) определяется тремя слагаемыми:  , ,где Кp, Кi, Кd - коэффициенты усиления пропорциональной, интегральной и дифференциальной составляющих регулятора, соответственно. Большинство методов настройки ПИД-регуляторов используют несколько иную формулу для выходного сигнала, в которой на пропорциональный коэффициент усиления умножены также интегральная и дифференциальная составляющие: 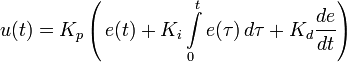 Часто в качестве параметров ПИД-регулятора используются: относительный диапазон 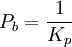 постоянные интегрирования и дифференцирования, имеющие размерность времени  В соответствии с рис.1 и рис.2 схему САР с ПИД-регулятором можно представить в виде, изображенном на рис.3.  Рис.3. САР с ПИД-регулятором. Для анализа САР предположим, что объект регулирования представляет собой инерционное или апериодическое звено. Каждое звено САР, представленной на рис.3, имеет свое уравнение и передаточную функцию (см. таблицу 1). Таблица 1 – Уравнения и передаточные функции звеньев САР
Примечание: Т1 – постоянная времени инерционного звена; T2 – постоянная интегрирования; T3 – постоянная дифференцирования; k1 – коэффициент усиления инерционного звена; k2 – коэффициент усиления пропорционального звена. Структурная схема САР и передаточные функции ее звеньев позволяют построить эквивалентную схему и ее передаточную функции в соответствии с правилами, приведенными в таблице 2. Таблица 2 – Преобразования структурных схем САР 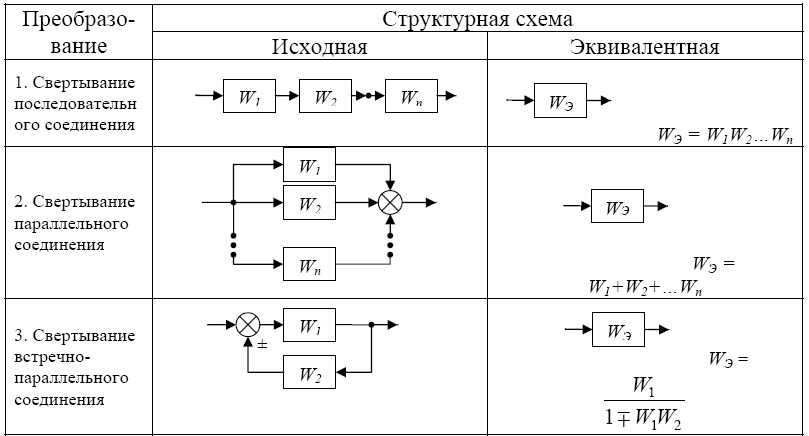 Руководствуясь данными таблицы 1 и правилами таблицы 2, составим передаточные функции П, ПИ, ПД и ПИД регуляторов и соответствующих САР с инерционным объектом регулирования. Выражения для передаточных функций сведем в таблицу 3. Таблица 3 – Передаточные функции регулятора и САР
Приведенные передаточные функции позволяют получить переходные характеристики САР. 2. Построение переходных характеристик САР обратным преобразованием Лапласа. Построить переходную характеристику САР для типового (например, скачкообразного или ступенчатого) воздействия можно путем обратного преобразования Лапласа произведения передаточной функции САР на изображение воздействия. Изображением единичного ступенчатого воздействия (ступенчатого изменения задающего воздействия) является выражение: 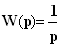 . .Тогда реакция САР на это воздействие будет описываться передаточной функцией: - для пропорционального регулятора:  , ,- для пропорционально-интегрального регулятора: 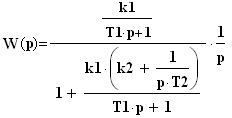 , ,- для пропорционально-дифференциалного регулятора:  , ,- для пропорционально-интегрально-дифференциального регулятора: 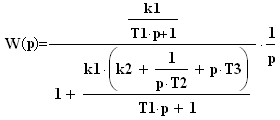 . .Применив к указанным передаточным функциям обратное преобразование Лапласа, получим выражения переходных характеристик САР для единичного ступенчатого воздействия. Обратное преобразование можно получить в Mathcad, используя команду меню Symbolics –> Transform -> Inverse Laplaсе. Для выполнения команды следует создать выражение передаточной функции, выбрать курсором переменную р и выполнить команду меню. На рис.4 приведен пошаговый пример получения переходной характеристики для САР с П-регулятором: 1) построение выражения для передаточной функции, выбор переменной р и выполнение команды Symbolics –> Transform -> Inverse Laplaсе; 2) результат выполнения команды Symbolics –> Transform -> Inverse Laplaсе; 3) построение выражения для переходной характеристики (функция Y1(t)). 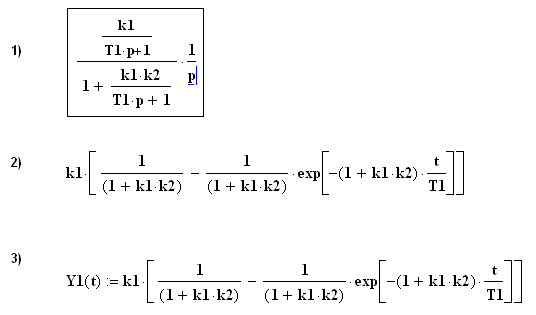 Рис.4. Порядок получения переходной характеристики По результатам построения переходных характеристик можно получить их реализации для различных значений параметров звеньев САР (постоянных Т1, Т2, Т3, k1, k2). Для этого следует задаться численными значениями постоянных, задать промежуток времени наблюдения переходного процесса САР и построить графики изменения функций Y(t) (см. пример на рис.5).  Рис.5. Графики переходных процессов САР Y(t) – единичное ступенчатое воздействие; Y1(t) – САР с П-регулятором; Y2(t) – САР с ПИ-регулятором; Y3(t) – САР с ПД-регулятором; Y4(t) – САР с ПИД-регулятором; Порядок выполнения работы. В соответствии с полученным вариантом задания (см. таблицу 4) выполнить следующие работы. 1). Построить переходные характеристики САР с П, ПИ, ПД и ПИД регуляторами, используя операцию обратного преобразования Лапласа. Результат расчета представить графически (см. рис.5). 2). По графикам переходных характеристик определить показатели качества процесса регулирования: время регулирования, величину перерегулирования, число колебаний за время регулирования, период колебаний. Таблица 4 – Варианты задания коэффициентов передаточной функции САР
Содержание отчета 1. Наименование работы. 2. Цель работы. 3. Задание на работу. 4. Вывод передаточных функций САР с П, ПИ, ПД, ПИД регуляторами для объекта регулирования – инерционного звена. 5. Порядок получения переходной характеристики САР с использованием обратного преобразования Лапласа. 6. Графики переходных процессов САР для полученного варианта задания. 7. Количественные оценки показателей качества процесса регулирования. Контрольные вопросы 1. Свойства пропорционального звена. 2. Свойство интегрирующего звена. 3. Свойства дифференцирующего звена. 4. Свойства инерционного звена. 5. Что такое обратная связь? 6. Что такое передаточная функция? 7. Что такое переходная характеристика? |