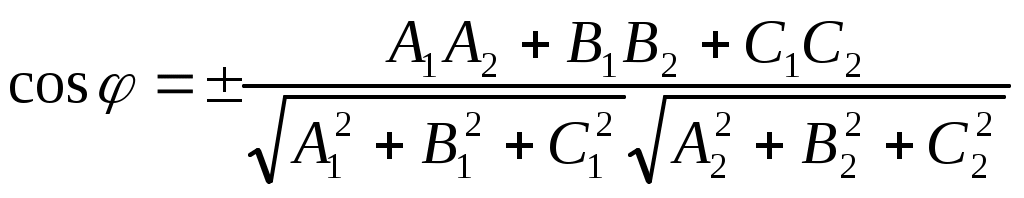Лекция.+Уравнение+плоскости. Лекция Уравнение плоскости в пространстве Общее уравнение плоскости
 Скачать 225 Kb. Скачать 225 Kb.
|
|
Лекция: Уравнение плоскости в пространстве Общее уравнение плоскости Плоскостью называется поверхность, все точки которой удовлетворяют уравнению Ax + By + Cz + D = 0, где А, В, С – координаты вектора Возможны следующие частные случаи: А = 0 – плоскость параллельна оси Ох В = 0 – плоскость параллельна оси Оу С = 0 – плоскость параллельна оси Оz D = 0 – плоскость проходит через начало координат А = В = 0 – плоскость параллельна плоскости хОу А = С = 0 – плоскость параллельна плоскости хОz В = С = 0 – плоскость параллельна плоскости yOz А = D = 0 – плоскость проходит через ось Ох В = D = 0 – плоскость проходит через ось Оу С = D = 0 – плоскость проходит через ось Oz А = В = D = 0 – плоскость совпадает с плоскостью хОу А = С = D = 0 – плоскость совпадает с плоскостью xOz В = С = D = 0 – плоскость совпадает с плоскостью yOz Уравнение плоскости, проходящей через данную точку, перпендикулярно данному вектору 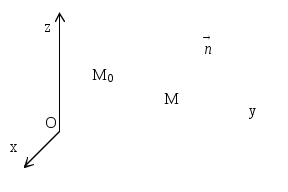 Если в пространстве задана точка М0(х0, у0, z0), то уравнение плоскости, проходящей через точку М0 перпендикулярно вектору нормали Уравнение плоскости в отрезках Если в общем уравнении Ах + Ву + Сz + D = 0 поделить обе части на (-D) Ч 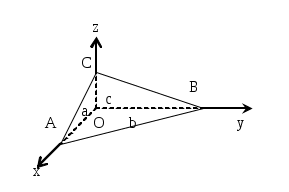 исла a, b, c являются точками пересечения плоскости соответственно с осями х, у, z. исла a, b, c являются точками пересечения плоскости соответственно с осями х, у, z. Уравнение плоскости в векторной форме (нормальное уравнение) Пусть 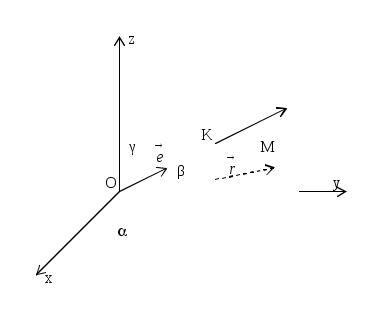 В координатах это уравнение имеет вид: xcos + ycos + zcos - p = 0, где Из общего уравнения можно перейти к нормальному уравнению, если умножить обе части уравнения на множитель Уравнение плоскости, проходящей через три точки Для того, чтобы через три какие- либо точки пространства можно было провести единственную плоскость, необходимо, чтобы эти точки не лежали на одной прямой. Рассмотрим точки М1(x1, y1, z1), M2(x2, y2, z2), M3(x3, y3, z3) в общей декартовой системе координат. Для того, чтобы произвольная точка М(x, y, z) лежала в одной плоскости с точками М1, М2, М3 необходимо, чтобы векторы 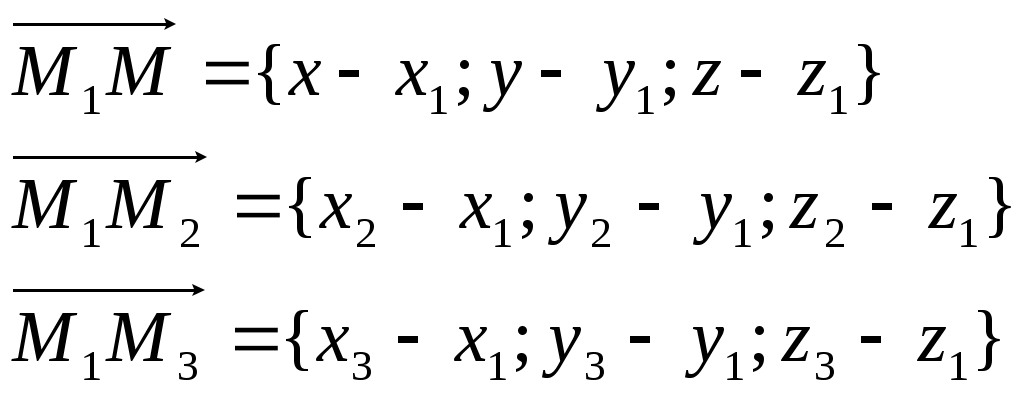 Уравнение плоскости, проходящей через три точки:  Пример. Найти уравнение плоскости, проходящей через точки Воспользуемся выше предложенной формулой:  Получаем уравнение плоскости Уравнение плоскости по двум точкам и вектору, коллинеарному плоскости Пусть заданы точки М1(x1, y1, z1), M2(x2, y2, z2) и вектор |
| 1. | 5. | 9. |
| 2. | 6. | 10. |
| 3. | 7. | 11. |
| 4. | 8. | 12. |
Определите, какая из них:
- параллельна осям Ох, Оу, Оz,
- проходит через начало координат,
- параллельна плоскостям хОу, хОz, yOz,
- проходит через оси Ох, Оу, Oz
- совпадает с плоскостями хОу, xOz, yOz.
2. Проходит ли плоскость
3. Может ли плоскость проходить через четыре заданные точки?
4. Определите нормаль к плоскостям
5. Найдите объём пирамиды, ограниченной плоскостью
6. Установите соответствие между плоскостью и ее уравнением:
| | общее уравнение |
| | нормальное уравнение |
| | уравнение в отрезках |
| | |
7. Найдите уравнение плоскости, проходящей через основание перпендикуляров, опущенных из точки М(2;2;2) на координатные плоскости.
8. Постройте плоскости
9. Установите, как расположены между собой плоскости:
| | параллельны |
| | перпендикулярны |
| | пересекаются под углом |
10. Пересекаются ли плоскости
11. Составьте уравнение плоскости проходящей через линию пересечения плоскостей

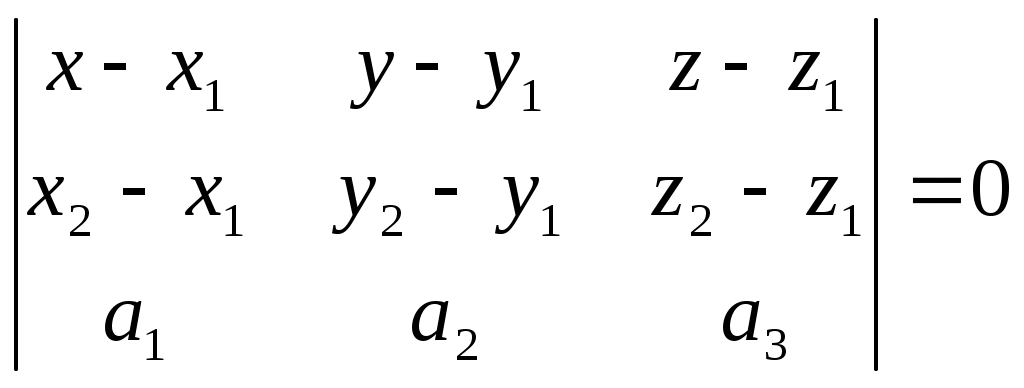
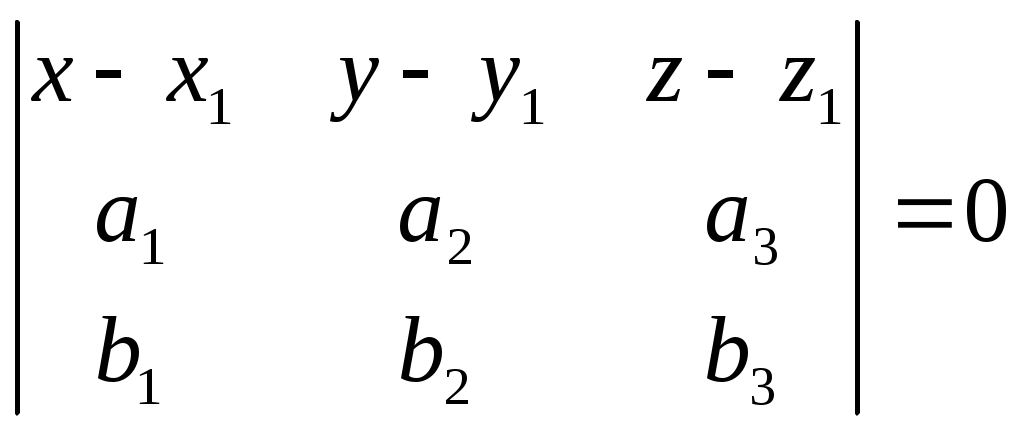 .
.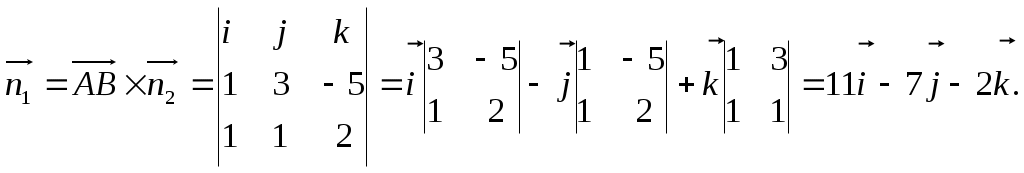
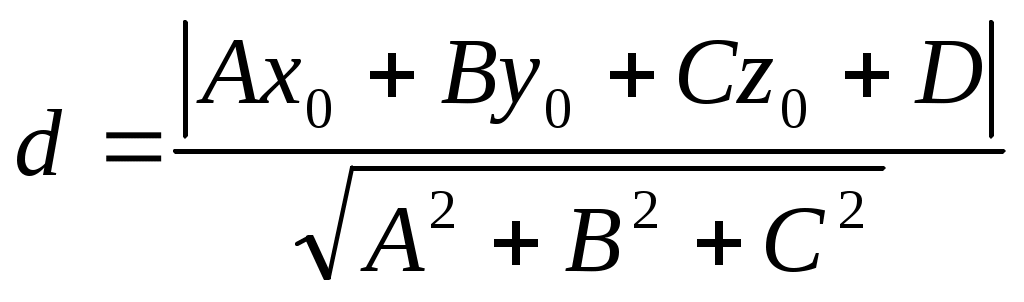
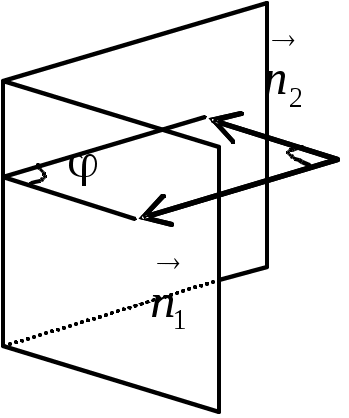
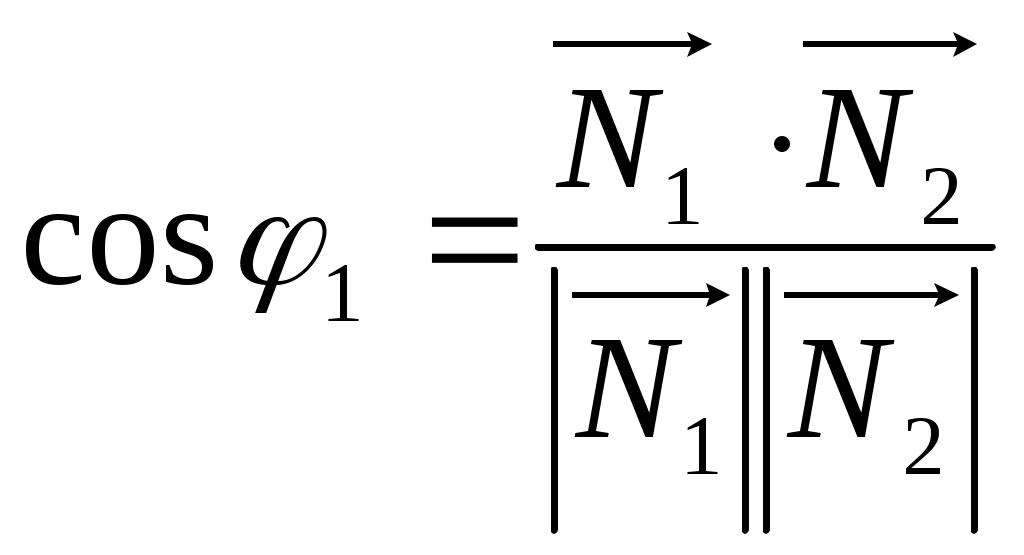 . Таким образом, угол между плоскостями находится по формуле:
. Таким образом, угол между плоскостями находится по формуле: