лекция матеиатика. Лекция №05 (2 семестр). Линейные дифференциальные уравнения высших порядков

• Название: Линейные дифференциальные уравнения высших порядков
• Анкор: лекция матеиатика
• Дата: 05.09.2022
• Размер: 300 Kb.
• Имя файла: Лекция №05 (2 семестр).doc
• Тип: Задача; #662783

Тема: Линейные дифференциальные уравнения высших порядков

1. 
   Общие понятия. Задача Коши
   

Многие задачи математики, механики, электротехники и других технических наук приводят к линейным дифференциальным уравнениям.

Уравнение вида

, (1.1)

в котором , , ,…, – заданные на отрезке функции, называется линейным неоднородным дифференциальным уравнением (ЛНДУ)n-го порядка.

Если , , то уравнение

(1.2)

называется линейным однородным дифференциальным уравнением (ЛОДУ)n-го порядка.

Задача Коши для уравнения (1.1) формулируется следующим образом: найти решение уравнения (1.1), удовлетворяющее начальным условиям

, (1.3)

где – заданные числа; .

Теорема 1.1.Пусть на отрезке коэффициенты , , и правая часть уравнения (1.1) непрерывны. Тогда:

1) решение задачи Коши (1.1), (1.3) существует на всём отрезке ;

2) если два решения и уравнения (1.1) удовлетворяют одним и тем же начальным условиям (1.3), то , .

Следствие. Пусть – решение линейного однородного дифференциального уравнения (1.2), удовлетворяющее нулевым начальным условиям

.

Тогда , .

Обозначим

. (1.4)

Оператор называется линейным дифференциальным оператором (ЛДО). С его помощью дифференциальные уравнения (1.1) и (1.2) записываются в виде

(1.5)

и

(1.6)

соответственно.

2. 
   Линейная независимость функций. Определитель Вронского
   

Напомним, что функции называются линейно зависимыми на интервале , если существуют постоянные числа , не все из которых равны нулю, такие, что

, . (2.1)

Если же равенство (2.1) имеет место только при , то функции называются линейно независимыми на интервале .

Определяющую роль в выяснении линейной зависимости системы функций 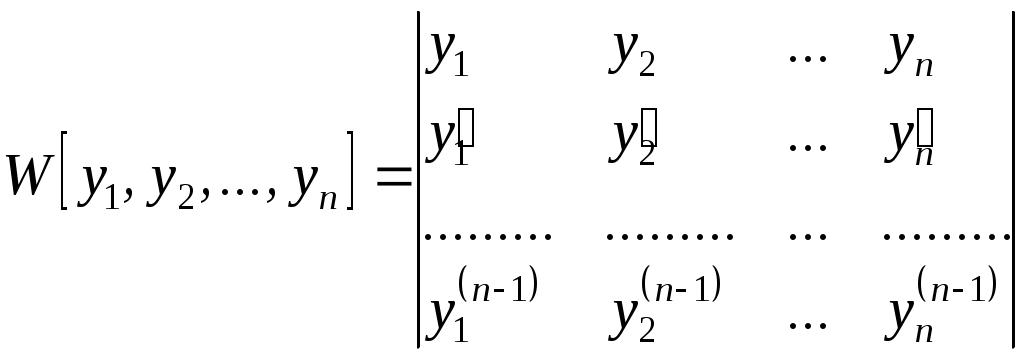класса играет определитель Вронского¹, или вронскиан

. (2.2)

Если функции и их первые производные вычисляются в точке , то значение вронскиана в этой точке будет обозначаться .

Теорема 2.1.Если функции класса линейно зависимы, то , .

Следствие (достаточное условие линейной независимости функций). Если хотя бы в одной точке определитель Вронского функций отличен от нуля, то эти функции линейно независимы на интервале .

Пример 2.1. Можно показать, что функции линейно независимы на любом интервале .

Пример 2.2. Если – различные числа, то функции линейно независимы на любом интервале .

Пример 2.3. Функции линейно независимы на любом интервале .

3. 
   Структура общего решения линейного однородного дифференциального уравнения
   

Теорема 3.1 (о структуре общего решения линейного однородного дифференциального уравнения). Всякое линейное однородное дифференциальное уравнение порядка имеет ровно линейно независимых решений , . Общее решение этого уравнения имеет вид

, (3.1)

где – некоторые постоянные.

Всякая система линейно независимых решений линейного однородного дифференциального уравнения порядка называется фундаментальной системой решений этого уравнения.

4. 
   Структура общего решения линейного неоднородного дифференциального уравнения
   

Теорема 4.1 (о структуре общего решения линейного неоднородного дифференциального уравнения). Общее решение линейного неоднородного дифференциального уравнения представляет собой сумму общего решения соответствующего однородного дифференциального уравнения и некоторого его частного решения , т.е.

. (4.1)

5. 
   Принцип суперпозиции решений
   

Можно показать, что если – решение уравнения , а – решение уравнения , то сумма есть решение уравнения .

Аналогично можно показать, что если функция , где – мнимая единица, есть решение уравнения ( , , и – действительные функции), то функции и являются решениями уравнений и соответственно.

Данное утверждение составляет суть принципа суперпозиции (наложения) решений. Очевидно, что принцип справедлив и для любого конечного числа решений, т.е. если – решение уравнения , то сумма является решением уравнения .

6. 
   Метод вариации (Лагранжа) произвольных постоянных (СРС)
   

Метод вариации позволяет найти общее решение линейного неоднородного дифференциального уравнения , если известна фундаментальная система решений соответствующего однородного уравнения , .

Пусть – фундаментальная система решений однородного уравнения . Тогда его общее решение имеет вид

, (6.1)

где – произвольные постоянные числа.

Общее решение неоднородного уравнения 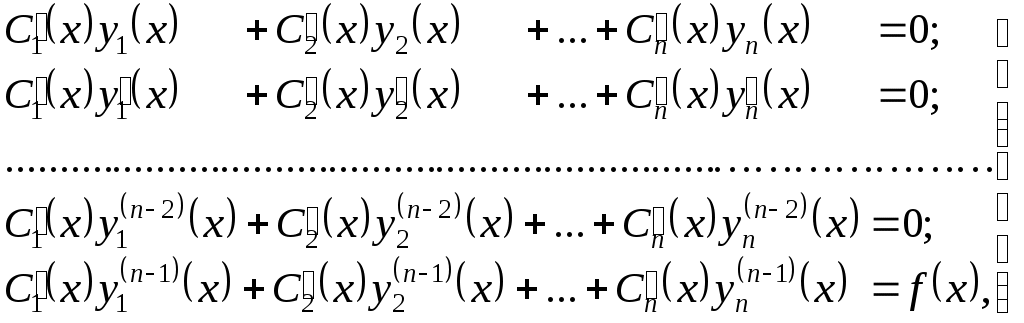будем искать в виде, сходном с функцией (6.1), считая, что коэффициенты являются уже не постоянными, а функциями от , т.е. общее решение ищем в виде

, (6.2)

где – гладкие функции , которые определяются из системы уравнений

(6.3)

являющейся неоднородной системой линейных алгебраических уравнений относительно функций . Определителем этой системы является вронскиан , так как – фундаментальная система решений однородного уравнения (1.2). Поэтому система (6.3) имеет единственное решение , , откуда , где – произвольные постоянные.

В частности, для уравнения второго порядка



система (6.3) имеет вид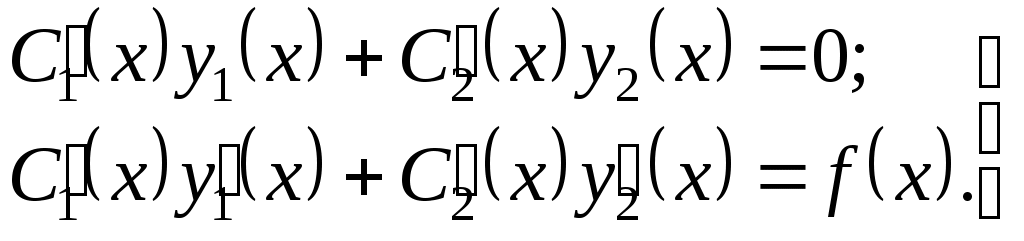



Решая её, например, по формулам Крамера, имеем

;

,

так что

; . (6.4)

Пример 6.1. Зная, что функции образуют фундаментальную систему решений уравнения , методом вариации решить уравнение .

D Искомое решение ищем в виде

.

Для определения функций 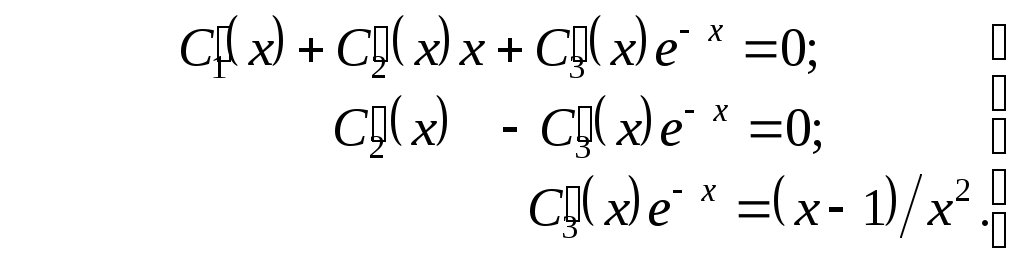составляем систему (6.3):



Из третьего уравнения системы находим

.

Тогда из второго уравнения имеем

.

Наконец, из первого уравнения получаем



.

Таким образом, общим решением исходного уравнения является функция



. ▲

1Ю. Гёне-Вронский (1776 – 1853) – польский математик.

© Гуров Владимир Владимирович, 2017