эконометрика. Линейные, нелинейные и множественные регрессии студент II курса
 Скачать 120.87 Kb. Скачать 120.87 Kb.
|
|
3. Критерий Дарбина-Уотсона. Этот критерий является наиболее известным для обнаружения автокорреляции. Для анализа коррелированности отклонений используют статистику Дарбина-Уотсона: Критические значения d1 и d2 определяются на основе специальных таблиц для требуемого уровня значимости α, числа наблюдений n = 20 и количества объясняющих переменных m=1. Автокорреляция отсутствует, если выполняется следующее условие: d1 Не обращаясь к таблицам, можно пользоваться приблизительным правилом и считать, что автокорреляция остатков отсутствует, если 1.5 Для более надежного вывода целесообразно обращаться к табличным значениям. По таблице Дарбина-Уотсона для n=20 и k=1 (уровень значимости 5%) находим: d1 = 1.20; d2 = 1.41. Поскольку 1.20 <1.73 и 1.41 <1.73 <4 - 1.41, то автокорреляция остатков отсутствует. 6. На одном графике отложить исходные данные итеоретическую прямую. 9.Проверить вычисления в MS Excel. 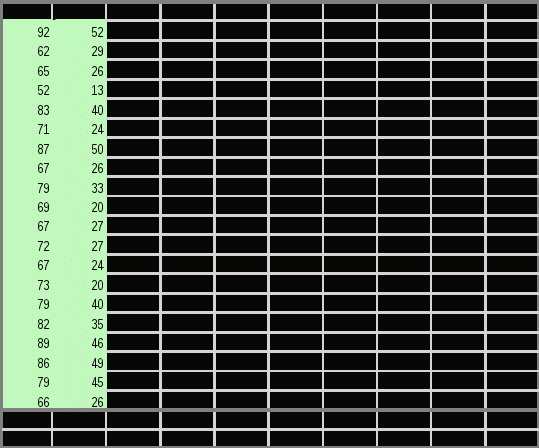  Выводы. Изучена зависимость Y от X. На этапе спецификации была выбрана парная линейная регрессия. Оценены её параметры методом наименьших квадратов. Статистическая значимость уравнения проверена с помощью коэффициента детерминации и критерия Фишера. Установлено, что в исследуемой ситуации 80.38% общей вариабельности Y объясняется изменением X. Установлено также, что параметры модели статистически значимы. Возможна экономическая интерпретация параметров модели - увеличение X на 1 ед.изм. приводит к увеличению Y в среднем на 0.983 ед.изм. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. При x=90, Y будет находиться в пределах от 36.24 до 59.74 ед.изм. и с вероятностью 95% не выйдет за эти пределы. Задача 2.
Требуется: 1. Построить линейную модель множественной регрессии. Записать стандартизованное уравнение множественной регрессии. На основе стандартизованных коэффициентов регрессии и средних коэффициентов эластичности ранжировать факторы по степени их влияния на результат. 2. Найти коэффициенты парной, частной и множественной корреляции. Проанализировать их. 3. Найти скорректированный коэффициент множественной детерминации. Сравнить его с нескорректированным (общим) коэффициентом детерминации. 4. С помощью F-критерия Фишера оценить статистическую надежность уравнения регрессии и коэффициента детерминации. p=90% 5. С помощью t-критерия Стьюдента оценить статистическую значимость параметров чистой регрессии. α = 0,01 6. Дисперсионный анализ модели множественной регрессии α = 0,05. 7. Проверьте наличие мультиколлинеарности в модели, вычислив значение показателя VIF, test Фарраром и Глаубером. α = 0,01. Проверить вычисления в MS Excel. Вывод и интерпретация. 1. Построить линейную модель множественной регрессии.Записать стандартизованное уравнение множественной регрессии. Наоснове стандартизованных коэффициентов регрессии и средних коэффициентов эластичности ранжировать факторы по степени их влиянияна результат. Система трех линейных уравнений с тремя неизвестными b0, b1, b2: ∑yi = nb0 + b1∑x1i + b2∑x2i ∑x1iyi = b0∑x1i + b1∑x1i2 + b2∑x1ix2i ∑x2iyi = b0∑x2i + b1∑x1ix2i + b2∑x2i2 Для удобства проведения расчетов поместим результаты промежуточных расчетов в таблицу:
Для наших данных система уравнений имеет вид: 28.8 = 15 b0 + 2014.5b1 + 845.3b2 7926 = 2014.5b0 + 774806.63b1 + 113751.26b2 1631.33 = 845.3b0 + 113751.26b1 + 47899.11b2 Решая систему методом Крамера, находим: b0 = -0.554, b1 = 0.00801, b2 = 0.0248 Уравнение регрессии: Y = -0.554 + 0.00801 X1 + 0.0248 X2 С целью расширения возможностей содержательного анализа модели регрессии используются частные коэффициенты эластичности, которые определяются по формуле: Частный коэффициент эластичности показывает, насколько процентов в среднем изменяется признак-результат у с увеличением признака-фактора хj на 1% от своего среднего уровня при фиксированном положении других факторов модели. Частный коэффициент эластичности |E1| <1. Следовательно, его влияние на результативный признак Y незначительно. Частный коэффициент эластичности |E2| <1. Следовательно, его влияние на результативный признак Y незначительно. Таким образом, влияние рыночной капитализации выше влияния численности служащих (Ex2> Ex1). 2. Найти коэффициенты парной, частной и множественнойкорреляции. Проанализировать их. Найдем средние квадратические отклонения признаков: = = Парные коэффициенты корреляции. Для y и x1 = Для y и x2 = Для x1 и x2 = На основании частных коэффициентов можно сделать вывод об обоснованности включения переменных в регрессионную модель. Если значение коэффициента мало или он незначим, то это означает, что связь между данным фактором и результативной переменной либо очень слаба, либо вовсе отсутствует, поэтому фактор можно исключить из модели. = Теснота связи сильная = Теснота связи низкая. = Теснота связи низкая. Межфакторная связь слабая. 3. Найти скорректированный коэффициент множественнойдетерминации. Сравнить его с нескорректированным (общим)коэффициентом детерминации. Объективную оценку качества построенной модели дает скорректированный индекс множественной детерминации, учитывающий поправку на число степеней свободы: где n - число наблюдений, m – число факторов. Коэффициент множественной корреляции можно определить через матрицу парных коэффициентов корреляции: где Δr - определитель матрицы парных коэффициентов корреляции; Δr11 - определитель матрицы межфакторной корреляции. Коэффициент множественной корреляции Аналогичный результат получим при использовании других формул: Связь между признаком Y и факторами Xi низкая. Расчёт коэффициента корреляции выполним, используя известные значения линейных коэффициентов парной корреляции и β-коэффициентов. Коэффициент детерминации R2 = 0.855 4. С помощью F-критерия Фишера оценить статистическуюнадежность уравнения регрессии и коэффициента детерминации R2. p=90% Проверка значимости модели регрессии проводится с использованием F-критерия Фишера, расчетное значение которого находится как отношение дисперсии исходного ряда наблюдений изучаемого показателя и несмещенной оценки дисперсии остаточной последовательности для данной модели. Если расчетное значение с k1=(m) и k2=(n-m-1) степенями свободы больше табличного при заданном уровне значимости, то модель считается значимой. R2 = 0.855 Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму: 1. Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H0: R2=0 на уровне значимости α. 2. Далее определяют фактическое значение F-критерия: где m=2 для множественной регрессии с двумя факторами. 3. Табличное значение определяется по таблицам распределения Фишера для заданного уровня значимости, принимая во внимание, что число степеней свободы для общей суммы квадратов (большей дисперсии) равно 2 и число степеней свободы остаточной суммы квадратов (меньшей дисперсии) при линейной регрессии равно n-2-1. 4. Если фактическое значение F-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу. В противном случае, нулевая гипотеза отклоняется и с вероятностью (1-α) принимается альтернативная гипотеза о статистической значимости уравнения в целом. Табличное значение критерия со степенями свободы k1=2 и k2=12, Fkp = 3.89 Поскольку фактическое значение F> Fkp, то коэффициент детерминации статистически значим (найденная оценка уравнения регрессии статистически надежна). 5. С помощью t-критерия Стьюдента оценить статистическуюзначимость параметров чистой регрессии.α = 0,01 Найдем парные коэффициенты корреляции.
Дисперсии и среднеквадратические отклонения. Рассчитаем наблюдаемые значения t-статистики для ryx1 по формуле: где m = 1 - количество факторов в уравнении регрессии. По таблице Стьюдента находим Tтабл tкрит (n-m-1; α/2) = (13;0.005) = 3.012 Поскольку tнабл> tкрит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически - значим Рассчитаем наблюдаемые значения t-статистики для ryx2 по формуле: Поскольку tнабл 6. Дисперсионный анализ модели множественной регрессии α = 0,05. Дисперсии и среднеквадратические отклонения.
7. Проверьте наличие мультиколлинеарности в модели, вычислив значение показателя VIF, testФарраром и Глаубером.α = 0,01. 1. Анализ мультиколлинеарности на основе матрицы коэффициентов корреляции. Если в матрице есть межфакторный коэффициент корреляции rxjxi> 0.7, то в данной модели множественной регрессии существует мультиколлинеарность. В нашем случае все парные коэффициенты корреляции |r| <0.7, что говорит об отсутствии мультиколлинеарности факторов. Анализ первой строки этой матрицы позволяет произвести отбор факторных признаков, которые могут быть включены в модель множественной корреляционной зависимости. Факторные признаки, у которых |ryxi| <0.5 исключают из модели. Можно дать следующую качественную интерпретацию возможных значений коэффициента корреляции (по шкале Чеддока): если |r|>0.3 – связь практически отсутствует; 0.3 ≤ |r| ≤ 0.7 - связь средняя; 0.7 ≤ |r| ≤ 0.9 – связь сильная; |r|> 0.9 – связь весьма сильная. Проверим значимость полученных парных коэффициентов корреляции с помощью t-критерия Стьюдента. Коэффициенты, для которых значения t-статистики по модулю больше найденного критического значения, считаются значимыми. Таким образом, связь между является существенной. Наибольшее влияние на результативный признак оказывает фактор x1 (r = 0.9222), значит, при построении модели он войдет в регрессионное уравнение первым. Более объективную характеристику тесноты связи дают частные коэффициенты корреляции, измеряющие влияние на результат фактора xi при неизменном уровне других факторов. 2. Ридж-регрессия. Наиболее детальным показателем наличия проблем, связанных с мультиколлинеарностью, является коэффициент увеличения дисперсии, определяемый для каждой переменной как: где Rj2 коэффициент множественной детерминации в регрессии Xj на прочие X. О мультиколлинеарности будет свидетельствовать VIF от 4 и выше хотя бы для одного j. Поскольку VIF(b)1 ≥ 4, что говорит о мультиколлинеарности факторов x1, x2 и о необходимости исключения одного из них из дальнейшего анализа. Наиболее полным алгоритмом исследования мультиколлинеарности является алгоритм Фаррара-Глобера. С его помощью тестируют три вида мультиколлинеарности: 1. Всех факторов (χ2 - хи-квадрат). 2. Каждого фактора с остальными (критерий Фишера). 3. Каждой пары факторов (критерий Стьюдента). 1. Проверим переменные на мультиколлинеарность методом Фаррара-Глобера по первому виду статистических критериев (критерий "хи-квадрат"). Формула для расчета значения статистики Фаррара-Глобера: χ2 = -[n-1-(2m+5)/6] ln(det[R]) = -[15-1-(2*2+5)/6] ln (0.145) = 24.11 где m = 2 - количество факторов, n = 15 - количество наблюдений, det[R] - определитель матрицы парных коэффициентов корреляции R. Сравниваем его с табличным значением при v = m/2(m-1) = 1 степенях свободы и уровне значимости α. Если χ2> χтабл2, то в векторе факторов присутствует мультиколлинеарность. χтабл2(1;0.01) = 6.63490 2. Проверим переменные на мультиколлинеарность по второму виду статистических критериев (критерий Фишера). Определяем обратную матрицу D = R-1: Вычисляем F-критерии Фишера: где dkk - диагональные элементы матрицы. Рассчитанные значения критериев сравниваются с табличными при v1=n-m и v2=m-1 степенях свободы и уровне значимости α. Если Fk> Fтабл, то k-я переменная мультиколлинеарна с другими. v1=15-2 = 14; v2=2-1 = 2. Fтабл (14;2) = 99.43 Поскольку F1 ≤ Fтабл, то переменная y немультиколлинеарна с другими. Поскольку F2 ≤ Fтабл, то переменная x1 немультиколлинеарна с другими. Поскольку F3 ≤ Fтабл, то переменная x2 немультиколлинеарна с другими. 3. Проверим переменные на мультиколлинеарность по третьему виду статистических критериев (критерий Стьюдента). Для этого найдем частные коэффициенты корреляции. Можно сделать вывод, что при построении регрессионного уравнения следует отобрать факторы x1.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
