эконометрика. Линейные, нелинейные и множественные регрессии студент II курса
 Скачать 120.87 Kb. Скачать 120.87 Kb.
|
|
Выводы. В результате расчетов было получено уравнение множественной регрессии: Y = -0.5543 + 0.00801X1 + 0.02476X2. Возможна экономическая интерпретация параметров модели: увеличение X1 на 1 ед.изм. приводит к увеличению Y в среднем на 0.00801 ед.изм.; увеличение X2 на 1 ед.изм. приводит к увеличению Y в среднем на 0.0248 ед.изм. По максимальному коэффициенту β1=0.921 делаем вывод, что наибольшее влияние на результат Y оказывает фактор X1. Задача 3. Модель парнойнелинейной регрессии. Имеются данные по группе акционерных коммерческих банков региона.
Задания 1. Постройте поле корреляции и сформулируйте гипотезу о форме связи. Рассчитайте параметры уравнений показательной ( 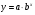 ) и гиперболической ( ) и гиперболической (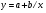 ) парной регрессии. ) парной регрессии.Совокупность точек результативного и факторного признаков называется полем корреляции. Для этого в прямоугольной системе координат строят график, по оси ординат откладывают индивидуальные значения результативного признака Y, а по оси абсцисс - индивидуальные значения факторного признака X. На основании поля корреляции можно выдвинуть гипотезу (для генеральной совокупности) о том, что связь между всеми возможными значениями X и Y носит показательный характер. Показательное уравнение регрессии имеет вид y = a*bx Для расчета параметров регрессии построим расчетную таблицу (табл. 1)
Для наших данных система уравнений имеет вид 10a + 3179·b = 15.934 3179·a + 1806091·b = 5293.733 Домножим уравнение (1) системы на (-317.9), получим систему, которую решим методом алгебраического сложения. -3179a -1010604.1 b = -5065.311 3179*a + 1806091*b = 5293.733 Получаем: 795486.9*b = 228.422 Откуда b = 0.000287 Теперь найдем коэффициент «a» из уравнения (1): 10a + 3179*b = 15.934 10a + 3179*0.000287 = 15.934 10a = 15.021 a = 1.5021 Получаем эмпирические коэффициенты регрессии: b = 0.000287, a = 1.5021 Уравнение регрессии (эмпирическое уравнение регрессии): y = 101.5021*100.000287x = 31.77491*1.00066x Параметры уравнения регрессии. Выборочные средние. Выборочные дисперсии: = = Среднеквадратическое отклонение Коэффициент корреляции b можно находить по формуле, не решая систему непосредственно: Эмпирическое корреляционное отношение вычисляется для всех форм связи и служит для измерения тесноты зависимости. Изменяется в пределах [0;1]. Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока: 0.1 <η <0.3: слабая; 0.3 <η <0.5: умеренная; 0.5 <η <0.7: заметная; 0.7 <η <0.9: высокая; 0.9 <η <1: весьма высокая; где Полученная величина свидетельствует о том, что фактор x существенно влияет на y Также на основании поля корреляции можно выдвинуть гипотезу (для генеральной совокупности) о том, что связь между всеми возможными значениями X и Y носит гиперболический характер. Гиперболическое уравнение регрессии имеет вид y = b/x + a Для расчета параметров регрессии построим расчетную таблицу (табл. 1)
Для наших данных система уравнений имеет вид 10a + 0.0573·b = 401.8 0.0573·a + 0.00045·b = 2.044 Домножим уравнение (1) системы на (-0.00573), получим систему, которую решим методом алгебраического сложения. -0.0573a -0.000328 b = -2.302 0.0573*a + 0.00045*b = 2.044 Получаем: 0.000122*b = -0.258 Откуда b = -2131.1122 Теперь найдем коэффициент «a» из уравнения (1): 10a + 0.0573*b = 401.8 10a + 0.0573*(-2131.1122) = 401.8 10a = 523.913 a = 52.3921 Получаем эмпирические коэффициенты регрессии: b = -2131.1122, a = 52.3921 Уравнение регрессии (эмпирическое уравнение регрессии): y = -2131.1122 / x + 52.3921 Параметры уравнения регрессии. Выборочные средние. Выборочные дисперсии: = = Среднеквадратическое отклонение Коэффициент корреляции b можно находить по формуле, не решая систему непосредственно: Для оценки качества параметров регрессии построим расчетную таблицу (табл. 2)
Изучена зависимость Y от X. На этапе спецификации была выбрана парная гиперболическая регрессия. Оценены её параметры методом наименьших квадратов. Установлено также, что параметры модели статистически значимы. |
