|
|
107 6 класс. Линейное неравенство с одной переменной, содержащее переменную под знаком модуля
Поурочный план
Раздел:
|
Линейные неравенства с одной переменной
|
ФИО учителя:
|
|
Дата:
|
|
Класс: 6
|
Количество присутствующих
|
Количество отсутствующих
|
Тема урока:
|
Линейное неравенство с одной переменной, содержащее переменную под знаком модуля.
|
Цели обучения в соответствии с учебной программой:
|
6.2.2.15 изображать множество точек на координатной прямой, заданное неравенством вида |x| > a, |x| ≥ a, |x| < a, |x| ≤ a;
|
Цели урока:
|
Учащиеся будут
знать:
как изображать множество точек на координатной прямой, заданное неравенством вида
|x| > a, |x| ≥ a, |x| < a, |x| ≤ a;;
как записывать, используя математическую символику, ответы к решению неравенства;
уметь
изображать множество точек на координатной прямой, заданное неравенством вида
|x| > a, |x| ≥ a, |x| < a, |x| ≤ a;
использовать обозначения для записи числовых промежутков в ответах;
записывать решения неравенств в виде числового промежутка и записывать заданный числовой промежуток в виде неравенства.
|
Ход урока:
Этап урока, время
|
Действия учителя
|
Действия ученика
|
Оценивание
|
Ресурсы
|
Начало урока (орг.момент)
|
- приветствие учащихся
- психологический настрой
- проверка готовности учащихся к уроку
|
- приветствуют учителя
- настраиваются на урок
|
устный комментарий учителя
|
|
Начало урока (повторение, проверка дом.задания)
|
Проверить домашнее задание.
Совместно с учащимися определить тему и цели урока, "зону ближайшего развития".
|
Учащиеся проверяют домашнее задание самопроверкой по презентации
|
Похвала учителя
|
Презентация
|
Середина урока
|
Актуализация опорных знаний. Повторение. Устный опрос.
-Что называют модулем числа x? (Модулем числа x называется расстояние от начала координат до точки А(x))
-Как изобразить с помощью координатной прямой?
(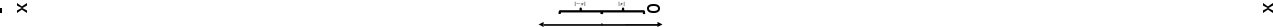 ) )
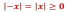
- Как записать математически определение модуля? (Определение модуля числа можно записать в виде:
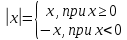 ) )
Модуль положительного числа равен самому числу.
Например:|3|= 3; | |= |=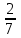 ; |2,4|= 2,4 ; |2,4|= 2,4
Модуль отрицательного числа равен противоположному ему числу.
Например: |-2| = -(-2)= 2; |-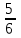 |= -(- |= -(-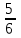 )= )=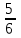
Модуль нуля равен нулю: |0|= 0.
- При каких значениях 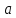 уравнение: уравнение: 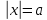 имеет: имеет:
а) один корень; (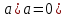 . .
б) два корня; (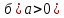 . .
в) не имеет корней? (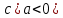 . .
-Назвать корни уравнений: а) 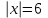 ; б) ; б) 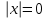 ; в) ; в) 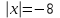 ; ;
Работа с классом.
Основываясь на знания: определение модуля, умение изображать с помощью координатной прямой данное расстояние от данной точки, изображать решение системы неравенств, ввести понятие линейного неравенства с одной переменной, содержащее переменную под знаком модуля и изображение решения неравенства.
Задание 1. Решить неравенство: 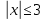 , то при , то при 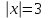 мы нашли решения, а для неравенства мы нашли решения, а для неравенства 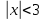 - решением будет интервал от -3 до 3. Окончательное решение: отрезок [-3;3]. - решением будет интервал от -3 до 3. Окончательное решение: отрезок [-3;3].
Т.е. неравенство графически можно изобразить так: расстояние от начала координат до точки 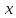 меньше числа меньше числа 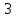 . Мы знаем, что точки можно откладывать в обе стороны от начала координат. Точка, которая находится на расстоянии . Мы знаем, что точки можно откладывать в обе стороны от начала координат. Точка, которая находится на расстоянии 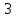 от начала координат, отложенного влево, имеет координату: от начала координат, отложенного влево, имеет координату: 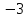 , точка, которая находится на расстоянии , точка, которая находится на расстоянии 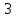 от начала координат, отложенного вправо, имеет координату:3.. Поскольку неравенство нестрогое, то концы промежутка входят в решение. от начала координат, отложенного вправо, имеет координату:3.. Поскольку неравенство нестрогое, то концы промежутка входят в решение.
Отрезок 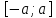 - это множество чисел - это множество чисел 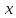 , удовлетворяющих двойному неравенству , удовлетворяющих двойному неравенству 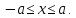
Следовательно, неравенство 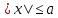 , где а>0, означает то же самое, что и двойное неравенство , где а>0, означает то же самое, что и двойное неравенство 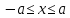 , которое можно записать в виде системы. , которое можно записать в виде системы.

Для строгих неравенств, например: 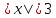 означает, что означает, что 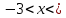 3 или 3 или 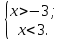
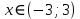 . .
Рассмотрим неравенство 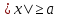 , где , где 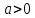 . .
Этому неравенству удовлетворяют все точки 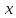 . находящиеся на расстоянии, не меньше . находящиеся на расстоянии, не меньше 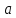 , от точки 0, т. е. точки двух лучей , от точки 0, т. е. точки двух лучей 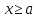 или или 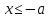 . Для правильного ответа эти лучи объединяют, используя знак объединения: . Объединение множеств есть совокупность неравенств, для записи используют . Для правильного ответа эти лучи объединяют, используя знак объединения: . Объединение множеств есть совокупность неравенств, для записи используют 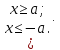
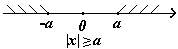
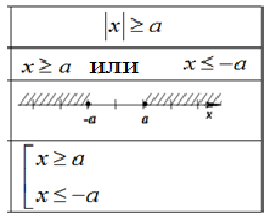
Например: |x| 3, равносильно х 3 или х -3, или если записать в виде совокупности, то 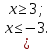
Обратить внимание учащихся.
1) Если в неравенстве 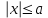 , число a=0, то неравенство имеет единственное решение , число a=0, то неравенство имеет единственное решение 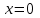 , а если , а если 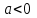 , то неравенство не имеет решений. , то неравенство не имеет решений.
2) Если в неравенстве 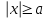 число число 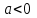 , то любое число является его решением, если a=0, то решение единственное , то любое число является его решением, если a=0, то решение единственное 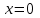 . .
Закрепление продолжить организовав работу групп, что дает возможность каждому оказать помощь с помощью наиболее продвинутых в математике учащихся.
|
Отвечают устно на вопросы учителя
Учащиеся рассуждают вместе с учителем и выводы записыают в тетрадь
|
устный комментарий учителя
|
(Данную табличку можно раздать каждому ученику до усвоения темы).
|
Середина урока
|
Групповая работа. Объединить учащихся в пары. Раздать каждой паре карточки с заданиями.
Приложение 1.
Задание 1. Изобразите на числовой прямой множество решений неравенства:
1) 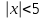 2) 2) 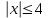 3) 3) 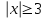 4) 4) 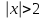
Задание 2. Запишите неравенство с модулем в виде двойного неравенства:
1) 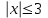 2) 2) 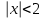
Задание 3. Двойное неравенство запишите в виде одного неравенства с модулем:
1) 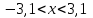 2) 2) 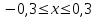
Задание 4. Множество чисел x, изображенное на рисунке, записать в виде двойного неравенства и неравенства, содержащего знак модуля.
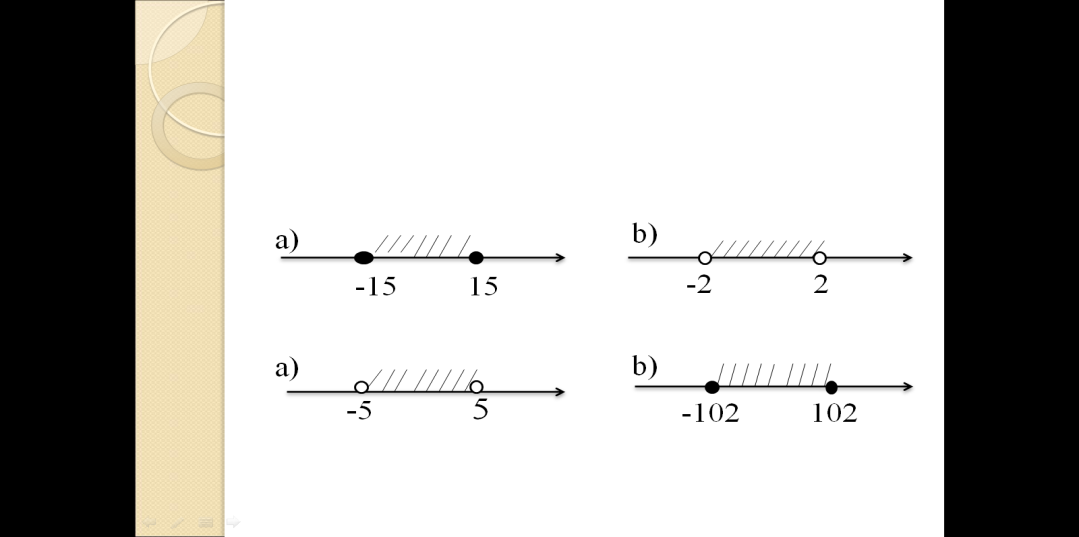
Учитель проходит по рядам, слушает, при необходимости задает дополнительные вопросы, корректирует решения учащихся, проверяет и оценивает похвалой работу групп, оказывает помощь слабоуспевающим.
Предоставить учащимся достаточно времени для выполнения заданий.
Проверить правильность ответов, провести анализ ошибок. Выслушать выводы учащихся по заданиям. Каждая группа демонстрирует свой результат выполнения заданий.
Старший группы оценивает вклад каждого, выставляя отметку.
|
Объединяются в пары и выполняют задания
|
Похвала учителя
|
Приложение 1.
|
Конец урока (подведение итогов, дом.задание)
|
Индивидуальная работа. Для закрепления и оценки усвоения пройденного материала предложить учащимся задания из учебного пособия уровня В, аналогичные заданиям, решенным при групповой работе или предложит задания Приложения 3. Каждый выполняет самостоятельно.
Приложение 2
Задание 1. Изобразите на числовой прямой множество решений неравенства:
1) 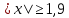 2) 2) 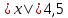 3) 3) 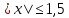 4) 4) 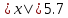
Задание 2. Запишите неравенство с модулем в виде двойного неравенства:
1) 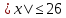 2) 2) 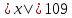
Задание 3. Двойное неравенство запишите в виде одного неравенства с модулем:
1) 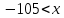 <105 2) <105 2) 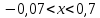
Задание 4. Множество чисел x, изображенное на рисунке, записать в виде двойного неравенства и неравенства, содержащего знак модуля.
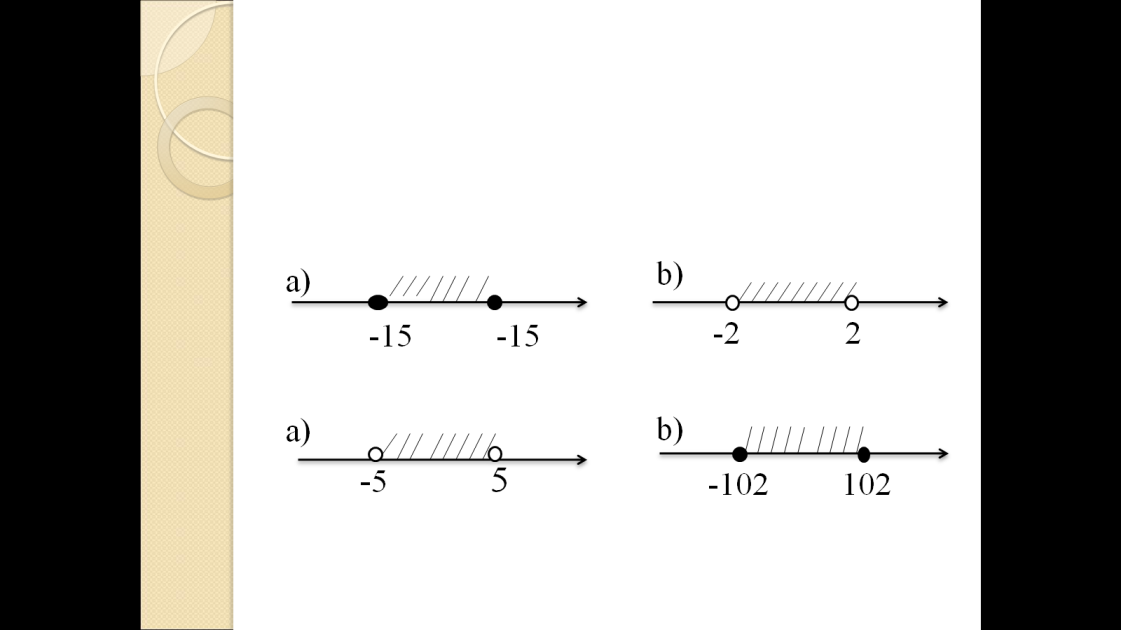
|
После окончания выполнения, попросить обменяться тетрадями с соседом. Взаимопроверка по ключу.
|
устный комментарий учителя
Собрать информацию о выполнении. Разобрать задания, которые были сделаны с ошибками.
|
Приложение 2
| |
|
|
 Скачать 366.95 Kb.
Скачать 366.95 Kb.