|
|
лин урав с двумя перемен. 17. Линейное уравнение с двумя переменными. Краткосрочный план. Линейное уравнение с двумя переменными
Краткосрочный план
6.4С Линейные уравнения с двумя переменными и их системы
|
Школа
|
Дата:
|
ФИО учителя: Нурсеитова З.Р.
|
Класс: 6
|
Количество
|
присутствующих:
|
отсутствующих:
|
Тема урока
|
Линейное уравнение с двумя переменными
|
Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу)
|
6.2.2.16
знать определение линейного уравнения с двумя переменными и его свойства;
|
Цели урока
|
Учащиеся будут
знать:
определение линейного уравнения с двумя переменными и его свойства
уметь
проверить является ли решением уравнения пара чисел;
выражать переменную у через переменную х путем выполнения тождественных преобразований..
|
Критерии оценивания
|
Учащиеся будут
знают:
определение линейного уравнения с двумя переменными и его свойства
умеют
проверить является ли решением уравнения пара чисел;
выражать переменную у через переменную х путем выполнения тождественных преобразований..
|
Языковые цели
|
Учащиеся будут:
аргументировать свои выводы, работая в группе, при повторении теоретического материала на более высоком уровне;
описывать ход своих действий и делать выводы;
при устной работе обосновывать ответ, используя терминологию.
Предметная лексика и терминология
линейное уравнение; решение линейного уравнения, пара чисел.
Полезные выражения для диалогов и письма: уравнения с двумя переменными называются линейными...,
Чтобы решить линейное уравнение надо... Выразить у через x...
|
Привитие ценностей
|
Умение учиться, добывать самостоятельно информацию, анализировать ситуацию, адаптироваться к новым ситуациям, ставить проблемы и принимать решения, работать в команде, отвечать за качество своей работы, умение организовывать свое время.
Привитие ценностей осуществляется посредством работ, запланированных на данном уроке.
|
Межпредметные связи
|
Взаимосвязь с жизнью, через решение практических задач.
|
Предварительные знания
|
Знание определение уравнения; решение линейного уравнения, свойства равносильных уравнений
|
Ход урока:
Запланированные этапы урока
|
Запланированная деятельность на уроке
|
Ресурсы
|
Начало урока
0 – 5 мин
|
Организационный момент. Актуализация опорных знаний.
Проверить домашнее задание.
Что называется линейным уравнением с двумя неизвестными?
Что значит решить уравнение с двумя неизвестными?
Сколько может быть решений у линейного уравнения?
Решите уравнение:
а) – 3х + 5 = 0;
б) – 0,5х + 1 = 0;
в) 4 = 2х – 3 .
Найдите значение выражения:
а) 6х + 5 при х = - 2; 0; 0,5;
б) – 2х – 3 при х = - 4; 0; 0,25.
Совместно с учащимися определить тему и цели урока, "зону ближайшего развития".
|
Презентация
|
Середина урока
6 - 15 мин
|
Работа с классом. В режиме диалога ввести определение и свойства линейного уравнения с двумя переменными в аналогии с линейным уравнением с одной переменной.
Уравнение с двумя переменными и его решение
Вид утверждения
|
Уравнения с одной переменной
|
Уравнения с двумя переменными
|
1) Пример
|
х + 5 = 8
|
х + у = 8
|
2) Описание
|
Равенство, содержащее неизвестное число, обозначенное буквой (переменная)
|
Равенство, содержащее два неизвестных числа, обозначенных буквой (переменные)
|
3) Сопутствующие понятия
|
Корень уравнения с первой переменной - значение переменной, превращает уравнение в верное равенство
|
Решение уравнения с двумя переменными - упорядоченная пара чисел (х;у), при которых уравнение превращается в верное равенство
|
4) Равносильны
|
уравнения с одной переменной - имеют одинаковые корни или не имеют корней
|
уравнения с двумя переменными - имеют одни и те же решения или оба не имеют решений
|
5) Свойства равносильных уравнений
|
Одинаковые
|
Учащиеся формулируют определения, сравнивают с текстом учебника, делают выводы.
Первичное закрепления знаний. Выработка умений решать задания по теме.
Вопросы к классу («Микрофон» или игровой момент «самый Умный»)
Приложение 1
1. Что называется решением уравнения с двумя переменными?
2. Является ли пара чисел (4; 1) решением уравнения х - 2у = 2?
3. Какие уравнения с двумя переменными называются равносильными?
4. Среди данных уравнений с двумя переменными выберите пары таких, что имеют одинаковые решения, и объясните, почему вы так считаете:
1) х + у = 2;
2) у = х + 2;
3) 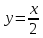 ; ;
4) 2у = х;
5) у = -х + 2.
Учащиеся формулируют определения, сравнивают с текстом учебника, делают выводы.
|
Приложение 1
|
|
Середина урока
16 - 25 мин
|
Работа в парах. Взаимное обучение. Создать пары из представителей разных групп. Предложить ученикам процесс взаимного обучения: объяснить напарнику ход решения задания, затем вместе решить их. Определяем умение распределять обязанности в паре.
Приложение 2
Выполнение письменных упражнений:
1. Какие из пар чисел (2; 2); (1; 3); (1; 3,5); (4; -1) являются решениями уравнения
3х + 2у = 10?
2. Выразите у через х в уравнениях и найдите два каких-нибудь решения уравнения:
1) х - у = 7; 2) 3х + 2у = 5; 3) 5х - 2у = 8; 4) 2х - 5у = 7; 5) 3х + 2у = 10.
Предоставить достаточно времени для выполнения задания.
Подвести итог после решения этих заданий.
Пригласите к доске ученика, попросите его записать подробное решение задания. Учащиеся на местах решают все примеры и сверяют свои решения с записями на доске, внимательно слушают одноклассников. С целью развития математической речи попросите одного из учащихся подробно прокомментировать решение любого задания, акцентируйте их внимание на обоснование решений. Для учащихся с более высокой скоростью решения организуйте "уголок Знайки", куда они могли бы подходить и проверять свое решение или читать идею решения. Это позволяет не отвлекаться на объяснение задачи, а работать в это время с остальной частью класса.
При наличии компьютера, просмотреть презентацию для визуального закрепления материала.
|
Приложение 2
|
Середина урока
26 - 37 мин
|
Групповая работа. Объединить учащихся в разноуровневые малые группы. Раздать каждой группе карточки с заданиями.
Приложение 3
1) Является ли решением уравнения х - 2у = 6 пара чисел (0; 0); (2; -2); (8; 1); (0; 3); (15; 4); (6; 0); (5; -5,5)?
2) Выразите переменную у через переменную х путем выполнения тождественных преобразований:
а) х + у = 1;
б) 5х + 5у = 0;
в) х - у = 2. По заданной формуле найдите два решения каждого уравнения.
3) Назовите коэффициенты a, b и c линейного уравнения.
а) x - 3у = 6; б) x - 2у = 0; в) 1,5 х = 6;
г) -0,3 = 0,6; д) 5х - 6у = 4; е) 8х + 16у = 24.
4) Выразите из уравнения переменную у через переменную х. Используя созданную формулу, найдите три каких-либо решения уравнения:
а) х + у = 27; б) 2х - у = 4,5;
в) 3х + 2у = 12; г) 5у - 2х = 1.
Учитель проходит по рядам, слушает, при необходимости задает дополнительные вопросы, корректирует решения учащихся, проверяет и оценивает похвалой работу групп, оказывает помощь слабоуспевающим.
Предоставить учащимся достаточно времени для выполнения заданий.
Проверить правильность ответов, провести анализ ошибок. Выслушать выводы учащихся по заданиям. Каждая группа демонстрирует свой результат выполнения заданий.
Старший группы оценивает вклад каждого, выставляя отметку.
|
Приложение 3
|
Конец урока
38 - 40 мин
|
Беседа. Рефлексия.
В конце урока учащиеся проводят рефлексию, прикрепляя стикер со своим именем на слайде и или на бумаге, прикрепленной к доске.

Домашнее задание. Знать определения, решить из уровня В учебного пособия "Математика 6" №...№.
|
|
Дифференциация – каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися?
|
Оценивание – как Вы планируете проверить уровень усвоения материала учащимися?
|
Здоровье и соблюдение техники безопасности. Связи с ИКТ.
|
На уроке предусмотрена дифференциация в виде работы в разнородных парах (разного уровня обучаемости).
|
Предусмотрена взаимопроверка по ключу, в ходе которой оценивается умение учеников применять теоретические знания. В ходе групповой деятельности при выполнении задании оцениваются умение находить результат, а также решать задания по теме, опираясь на понятие и свойства, изученные на данном уроке и прошлый опыт.
|
Запланированы виды деятельности на уроке, способствующие передвижению учащихся по классу, поэтому необходимо обеспечить безопасность. Следить за осанкой учащихся.
| |
|
|
 Скачать 90.42 Kb.
Скачать 90.42 Kb.