Реферат на тему Евклида. Реферат на тему. Литература Алгоритм Евклида алгоритм для нахождения наибольшего общего делителя двух целых чисел или наибольшей общей меры двух однородных величин.
 Скачать 44.21 Kb. Скачать 44.21 Kb.
|
|
Введение 1 История…………………………………………………………………………3 2 Алгоритм Евклида для целых чисел………………………………………4 3 Пример………………………………………………………………………5 4 Расширенный алгоритм Евклида и соотношение Безу…………………...6 4.1 Связь с цепными дробями………………………………………....7 5 Вариации и обобщения……………………………………………………..8 5.1 Обобщённый алгоритм Евклида для многочленов………………9 5.2 Ускоренные версии алгоритма……………………………………11 Литература Алгори́тм Евкли́да — алгоритм для нахождения наибольшего общего делителя двух целых чисел или наибольшей общей меры двух однородных величин. 1. История Древнегреческие математики называли этот алгоритм ἀνθυφαίρεσις или ἀνταναίρεσις — «взаимное вычитание». Этот алгоритм не был открыт Евклидом, так как упоминание о нём имеется уже в Топике Аристотеля. В «Началах» Евклида он описан дважды — в VII книге для нахождения наибольшего общего делителя двух натуральных чисел и в X книге для нахождения наибольшей общей меры двух однородных величин. В обоих случаях дано геометрическое описание алгоритма, для нахождения «общей меры» двух отрезков. Историками математики (Цейтен и др.) было выдвинуто предположение, что именно с помощью алгоритма Евклида (процедуры последовательного взаимного вычитания) в древнегреческой математике впервые было открыто существование несоизмеримых величин (стороны и диагонали квадрата, или стороны и диагонали правильного пятиугольника). Впрочем, это предположение не имеет достаточных документальных подтверждений. Алгоритм для поиска наибольшего общего делителя двух натуральных чисел описан также в I книге древнекитайского трактата Математика в девяти книгах. Ряд математиков средневекового Востока (Сабит ибн Курра, ал-Махани, Ибн ал-Хайсам, Омар Хайям) попытались построить на основе алгоритма Евклида теорию отношений, альтернативную по отношению теории отношений Евдокса, изложенной в V книге «Начал» Евклида. Согласно определению, предложенному этими авторами, четыре величины, первая ко второй и третья к четвёртой, имеют между собой одно и то же отношение, если при последовательном взаимном вычитании второй величины в обеих парах на каждом шаге будут получаться одни и те же неполные частные. 2. Алгоритм Евклида для целых чисел Пусть a и b — целые числа, не равные одновременно нулю, и последовательность чисел определена тем, что каждое rk — это остаток от деления предпредыдущего числа на предыдущее, а предпоследнее делится на последнее нацело, то есть a = bq0 + r1 b = r1q1 + r2 r1 = r2q2 + r3 rk − 2 = rk − 1qk − 1 + rk rn − 1 = rnqn Тогда НОД(a,b), наибольший общий делитель a и b, равен rn, последнему ненулевому члену этой последовательности. Существование таких r1,r2,..., то есть возможность деления с остатком m на n для любого целого m и целого Корректность этого алгоритма вытекает из следующих двух утверждений: Пусть a = bq + r, тогда НОД (a,b) = НОД (b,r). Доказательство Пусть k — любой общий делитель чисел a и b, не обязательно максимальный, тогда a = t1 * k ; b = t2 * k; где t1 и t2 — целые числа из определения. Тогда k также общий делитель чисел b и r, так как b делится на k по определению, а r = a − bq = (t1 − t2 * q) * k (выражение в скобках есть целое число, следовательно, k делит r без остатка) Обратное также верно и доказывается аналогично пункту 2 - любой делитель b и r так же является делителем a и b. Следовательно, все общие делители пар чисел a,b и b,r совпадают. Другими словами, нет общего делителя у чисел a,b, который не был бы также делителем b,r, и наоборот. В частности, максимальный делитель остается тем же самым. Что и требовалось доказать. НОД (0,r) = r для любого ненулевого r. Проще сформулировать алгоритм Евклида так: если даны натуральные числа a и b и, пока получается положительное число, по очереди вычитать из большего меньшее, то в результате получится НОД. 3. Пример Для иллюстрации, алгоритм Евклида будет использован, чтобы найти НОД a = 1071 и b = 462. Для начала, от 1071 отнимем кратное значение 462, пока не получим знаменатель меньше чем 462. Мы должны дважды отнять 462, (q0 = 2), оставаясь с остатком 147 1071 = 2 × 462 + 147. Затем от 462 отнимем кратное значение 147, пока не получим знаменатель меньше чем 147. Мы должны трижды отнять 147 (q1 = 3), оставаясь с остатком 21. 462 = 3 × 147 + 21. Затем от 147 отнимем кратное значение 21, пока не получим знаменатель меньше чем 21. Мы должны семь раз отнять 21 (q2 = 7), оставаясь без остатка. 147 = 7 × 21 + 0. Так как последний остаток равен нулю, алгоритм заканчивается и НОД(1071, 462)=21. В табличной форме, шаги были следующие
4. Расширенный алгоритм Евклида и соотношение Безу Формулы для ri могут быть переписаны следующим образом: r1 = a + b( - q0) r2 = b − r1q1 = a( − q1) + b(1 + q1q0) НОД (a,b) = rn = as + bt здесь s и t целые. Это представление наибольшего общего делителя называется соотношением Безу, а числа s и t — коэффициентами Безу. Соотношение Безу является ключевым в доказательстве леммы Евклида и основной теоремы арифметики. 4.1. Связь с цепными дробями Отношение a / b допускает представление в виде цепной дроби: При этом цепная дробь без последнего члена равна отношению коэффициентов Безу t / s, взятому со знаком минус: Последовательность равенств, задающая алгоритм Евклида может быть переписана в форме 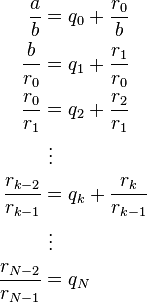 Последнее слагаемое в правой части равенства всегда равно обратному значению левой части следующего уравнения. Поэтому первые два уравнения могут быть объедены в форме 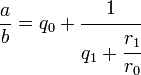 Третье равенство может быть использовано чтобы заменить знаменатель выражения r1/r0, получим 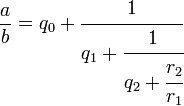 Последнее отношение остатков rk/rk−1 всегда может быть заменено используя следующее равенство в последовательности, и так до последнего уравнения. Результатом является цепная дробь 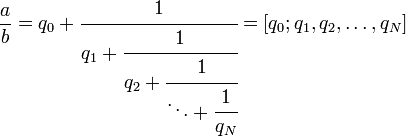 В приведённом выше примере, НОД(1071, 462) было посчитано и были найдены частные qk 2,3 и 7 соответственно. Поэтому, 1071/462 может быть записана как 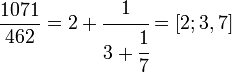 5. Вариации и обобщения Кольца, в которых применим алгоритм Евклида, называются евклидовыми кольцами. К ним относятся, в частности, кольца многочленов. 5.1. Обобщённый алгоритм Евклида для многочленов Алгоритм Евклида и расширенный алгоритм Евклида естественным образом обобщается на кольцо многочленов k[x] от одной переменной над произвольным полем k, и в частности над полем целых чисел (обозначим это кольцо Z[x]), поскольку для таких многочленов определена операция деления с остатком. При выполнении алгоритма Евклида для многочленов аналогично алгоритму Евклида для целых чисел, получается последовательность полиномиальных остатков (PRS). Пусть cont(f) по определению — НОД коэффициентов многочлена f(x) из Z[x] — содержание многочлена. Частное от деления f(x) на cont(f) называется примитивной частью многочлена f(x) и обозначается primpart(f(x)). эти определения понадобятся для нахождения НОД двух многочленов p1(x) и p2(x) в кольце Z[x]. Для многочленов над целыми числами верно следующее: cont(НОД{p1(x),p2(x)}) = НОД{cont(p1(x)),con(p2(x))}, primpart(НОД{p1(x),p2(x)}) = НОД{primpart(p1(x)),primpart(p2(x))}. Таким образом задача отыскания НОД двух произвольных многочленов сводится к задаче отыскания НОД примитивных полиномов. Пусть есть два примитивных многочлена p1(x) и p2(x) из Z[x], для которых выполняется соотношение между их степенями: deg(p1(x)) = m и deg(p2(x)) = n, m > n. Деление многочленов с остатком предполагает точную делимость старшего коэффициента делимого на старший коэффициент делителя, в общем случае деление с остатком выполнить невозможно. Поэтому вводят алгоритм псевдоделения, который всё же позволяет получить псевдочастное и псевдоостаток (prem), которые будут сами по себе принадлежать множеству многочленов над целыми числами. Под псевдоделением будем понимать, что самому делению предшествует умножение полинома p1(x) на (lc(p2(x)))m − n + 1, то есть lc(p2(x))m − n + 1p1(x) = p2(x)q(x) + r2(x), deg(r(x)) < deg(p2(x)), где q(x) и r(x) — соответственно псевдочастное и псевдоостаток. Итак, 1. Вычисление НОД содержаний: c: = НОД{cont(p1),cont(p2)}. 2. Вычисление примитивных частей: p1'(x): = cont(p1(x)); p2'(x): = cont(p2(x)). 3. Построение последовательности полиномиальных остатков: p1'(x), p2'(x), p3(x): = prem(p1'(x),p2'(x)), p4(x): = prem(p2'(x),p3(x)), p5(x): = prem(p3(x),p4(x)), ..., ph(x): = prem(ph − 2(x),ph − 1(x)). 4. Выход и возврат результата: Если deg(ph(x)) = 0, то вернуть c, иначе вернуть 5.2. Ускоренные версии алгоритма Одним из методов ускорения целочисленного алгоритма Евклида является использование симметричного остатка: где Одна из наиболее многообещающих версий ускоренного алгоритма Евклида для полиномов основывается на том, что промежуточные значения алгоритма в основном зависят от высоких степеней. Применение стратегии Разделяй и Властвуй позволяет уменьшить асимптотическую сложность алгоритма. Литература Виноградов И. М. Основы теории чисел. Курант Р., Роббинс Г. Дополнение к главе I, § 4. // Что такое математика?. — 3-e изд., испр. и доп.. — М., 2001. — 568 с. Абрамов С. Самый знаменитый алгоритм // Квант. — 1985. — № 11. — С. 44—46. Щетников А. И. Алгоритм Евклида и непрерывные дроби. Новосибирск: АНТ, 2003. Fowler D. H. The Mathematics of Plato’s Academy: a new reconstruction. 2nd ed. Oxford: Clarendon Press, 1999. von zur Gathen J., Gerhard J. Modern Computer Algebra. ISBN 0-521-82646-2 Панкратьев Е. В. Наибольший общий делитель и последовательности полиномиальных остатков // intuit.ru. |
