егнепобююдд.. Реология грунтов 2010 (2). Литература Бородавкин П. П. Механика грунтов, 3е издание, 2003г. Маслов Н. Н. Основы инженерной геологии и механики грунтов
 Скачать 0.65 Mb. Скачать 0.65 Mb.
|
|
Раздел 2. Определение напряжений в грунте оснований сооружений. Системы координат и характер задач, решаемых в механике грунтов. Существует плоская, пространственная и полярная системы координат (СК). В зависимости от характера нагрузок задача из пространственной может быть сведена к плоской. Некоторые плоские задачи можно свести к одномерной задаче.  Расчетные модели для определения напряжений в грунтах. Существуют 2 основные расчетные модели: 1) расчетная модель линейно-деформированного основания. 2) расчетная модель предельно-напряженного состояния. I модель исходит из предпосылки, что в точках основания нет необратимых сдвигов грунта; зависимость между деформациями и напряжениями – линейная. 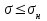 (7.6) (7.6)По этой модели определяют напряжения от собственного веса грунта при соблюдении условия (7.6). II модель соответствует концу II стадии напряженно-деформированного состояния, когда полностью исчерпывается прочность грунта. По этой модели рассчитывают прочность и устойчивость оснований. Расчетная модель линейно-деформированного основания. Она включает в себя основные силовые уравнения и вспомогательное условие, которым являются кривые неразрывности при деформировании грунта. Рассмотрим равновесие элемента под действием внутренних напряжений. 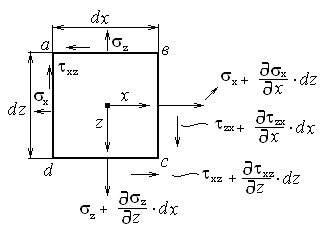 τxz =τzx z и x составляющие объемных сил. σx - составляющая нормальных напряжений в направлении оси x. τzx - касательная напряжения в площадке произвольного наклона в направлении осей х и z. Рассмотрим сумму проекций всех внутренних напряжений и составляющих объемных сил на оси x и z. Для этого сумма проекций всех сил приравнивается к нулю. 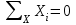 (*) (*) 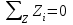 (**) (**)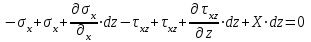 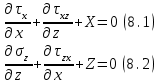  Для решения системы уравнения дополнительно записываются условия неразрывности, т.к. в данной расчетной модели деформации носят линейный характер, и сдвигов грунтов нет. 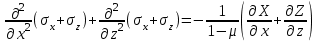 (8.3) (8.3)μ - коэффициент поперечной деформации грунта (аналогичен коэффициенту Пуассона). Уравнения (8.1) и (8.3) для решения некоторых задач удобно рассматривать в полярных координатах. Определение напряжений от собственного веса грунта. 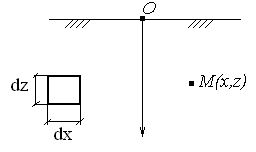
Используя уравнения (8.1), (8.2), (8.3) при следующих условиях: 1) поверхность грунта горизонтальна. 2) нет сдвигающих воздействий и погрузок. 3) площадки dx и dz будут являться главными при определений напряжений от собственного веса 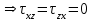 . .C учетом граничных условий: 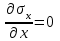 (8.4) (8.4)Из (8.2) следует: т.к. 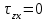 , то , то 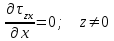 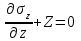 (8.5) (8.5)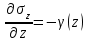 (8.6) (8.6)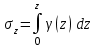 (8.7) – определение напряжения от собственного веса груза. (8.7) – определение напряжения от собственного веса груза.Из (8.3) следует: 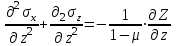 (8.8) (8.8)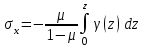 (8.9) (8.9)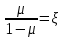 - коэффициент бокового давления грунта. - коэффициент бокового давления грунта.10. Однородное основание. 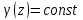 из (8.7) из (8.7) 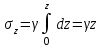 В (8.7) и (8.9) при γ=const, μ=const 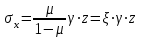 20. Слоистое основание. В (8.7) и (8.9) интегрирование заменяется суммированием по слоям. 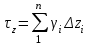 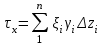 Определение напряжений от сосредоточенной силы. Задача Фламана. Задача решается в полярной системе координат. 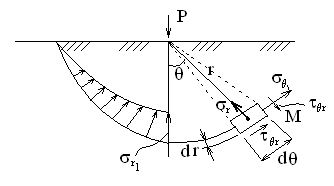  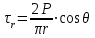 (9.1) (9.1)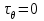 (9.2) (9.2)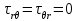 (9.3) (9.3) 1) при r=0, 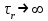 , даже при , даже при 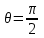 2) предположим, что 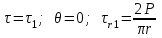 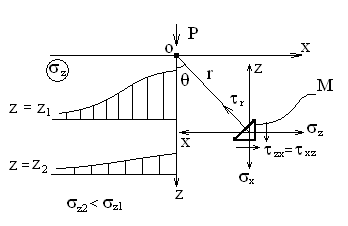 Из теории упругости известны соотношения между напряжениями прямоугольной и полярной СК. 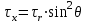 (9.4) (9.4)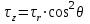 (9.5) (9.5)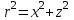 (9.6) (9.6)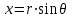 (9.7) (9.7)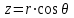 (9.8) (9.8)Используя соотношения (9.4) – (9.8) получим формулы для определения напряжений в прямоугольной СК. –  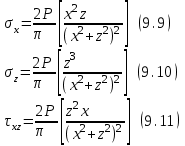 Используется как для решения практических Используется как для решения практических задач, так и для получения на основе расчетов формул для определения напряжений от распределенных нагрузок любых видов. Определение напряжений от равномерно распределенной нагрузки. Н 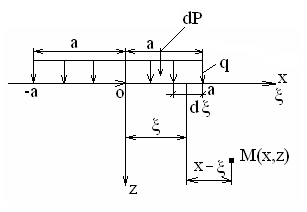 а практике много задач сводится к решению для случая, когда нагрузку можно считать равномерно распределенной по поверхности контакта сооружения с грунтом. Будем считать, что поверхность контакта находится на уровне начала координат. а практике много задач сводится к решению для случая, когда нагрузку можно считать равномерно распределенной по поверхности контакта сооружения с грунтом. Будем считать, что поверхность контакта находится на уровне начала координат.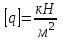 σx -? σz - ? σxz - ? Для решения задачи введем дополнительную ось координат, совпадающую с осью Оx. С 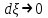 на пространство действует сила на пространство действует сила 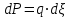 Используя принцип независимости действия сил (суперпозиции) определяем в т. М напряжения от сил dP и суммируем по всей ширине полосы загружения. Используя формулы (9.9) - (9.11) для сосредоточения силы можно записать: 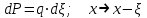 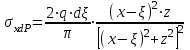 (9.12) (9.12)Интегрируя (9.12) по переменной 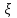 в пределах (-а;а) получим: в пределах (-а;а) получим: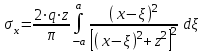 (9.13) (9.13)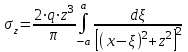 (9.14) (9.14)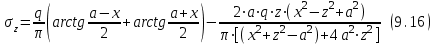  (9.17) αx, αz, ατ - табличные константы. (9.17) αx, αz, ατ - табличные константы. Определение напряжений по треугольной полосовой нагрузке. 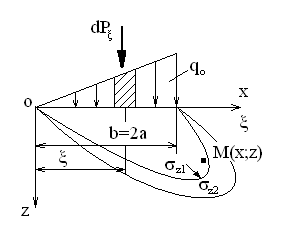 Используя решение для сосредоточенной силы, и применяя его к случаю сосредоточенной силы 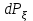 получаем зависимости для определения напряжений. получаем зависимости для определения напряжений.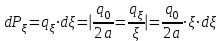 (*) (*)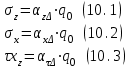  Рассмотрим изобары напряжений σz Определение напряжений от трапецеидальной полосовой нагрузки. 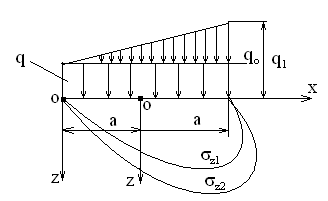 Задача решается с использованием принципа суперпозиции. Для этого трапеция делится на 2 части – на эпюру равномерно-распределенной нагрузки и на часть эпюры, где нагрузка распределена по треугольному закону. Для определения напряжений от равномерной нагрузки начало координат помещается в ц.т. подошвы (т.О). Для определения напряжений от ∆-ной части, начало координат помещается в ту краевую точку, где ордината эпюры ∆-ной нагрузки равна 0. 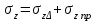 (10.4) (10.4)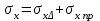 (10.5) (10.5)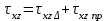 (10.6) (10.6)где σzΔ, σxΔ, τxzΔ – напряжение от треугольной части эпюры; σz пр, σх пр, τxz пр – напряжение от прямоугольной части эпюры. Определение напряжений по поверхностям контакта сооружений с грунтами. (самостоятельно) Классификация сооружений и решаемых задач в соответствии с собственной жесткостью конструкций. При взаимодействии сооружения – фундамент в зависимости от вида нагрузок и собственной изгибной жесткости сооружения по пов-ти контакта могут определятся как нормальные так и касательные напряжения. При этом в зависимости от изгибной жесткости все сооружения делятся на 3 группы: 1) «Абсолютно» жесткие сооружения – это те сооружения, изгибной деформацией которых можно пренебречь по сравнению с деформацией грунта. а) ленточные фундаменты под колонны при условии достаточного армирования, если при этом деформации изгиба малы. б) свайные основания при рассм. напряж. деформир. состояния ниже острия свай. 2) сооружения конечной жесткости – сооружения, собственные деформации которых сопоставимы с деформациями грунта. 3) совершенно гибкие сооружения – сооружения, в которых отсутствует собственная изгибная жесткость или ей можно пренебречь (нити, мембраны). Определение давления по подошве жесткого фундамента. 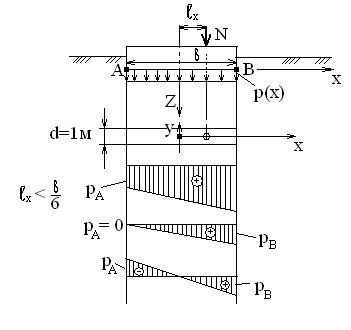 Рассмотрим задачу на примере ленточного фундамента. Рассмотрим решение с использованием формул внешего сжатия бруса из сопромата. 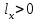 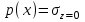 (10.7) (10.7)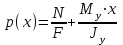 (10.8) (10.8)х - координата точки My - момент силы N относительно оси Оу. 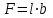 (10.9) (10.9) 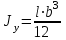 (10.10) (10.10) 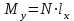 (10.11) (10.11)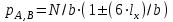 (10.12) (10.12)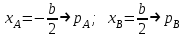 1) Как будет зависеть величина и знак pA от величины lx? Найдем граничное значение lx, при котором pA=0 (11.1) 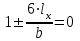 - в общем случае для обеих кривых точек. - в общем случае для обеих кривых точек.Для т.А: 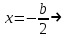 знак “–”, поэтому: знак “–”, поэтому: 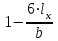 (11.2) (11.2)Из (11.2) получаем граничное значение lx: 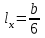 (11.3) (11.3)Для т. В: 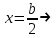 знак “+”, знак “+”, 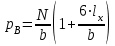 (*) (*)1) 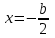 ; ; 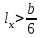 ; ; 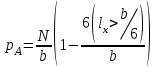 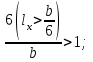 рА<0 рА<02) 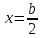 ; из (10.12) рB>0 ; из (10.12) рB>0При 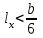 ; ; 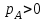 , , 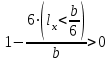 Поскольку большинство сооружений могут быть сведены к случаю жесткого сооружения, то формула (10.12) применима к расчету большинства сооружений в случае плоской задачи. Решение сопромата для внешнего сжатия дает значительные погрешности в следующих случаях: 1) очень больших значениях площади загружения. 2) когда невозможно пренебречь собственной деформацией конструкции. Распределение давления по подошве жестких сооружений по формулам теории упругости. При расчете жестких конструкций с большими размерами подошвы приходится уточнять распределение давления по подошве по формулам теории упругости. 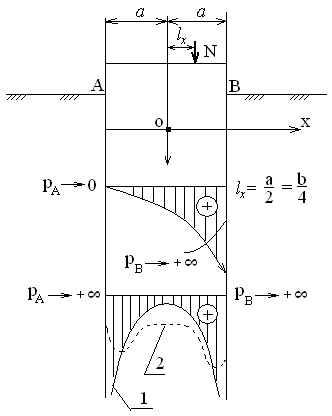 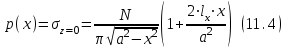 х=±а; (а2-х2)=0 а)  б)  при х=? при х=?Учитывая, что   , равенство нулю скобки возможно только при , равенство нулю скобки возможно только при  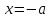 . .1) 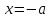 ; ;  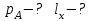 При каком граничном значении 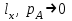 ? ?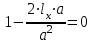 (**) (**)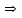 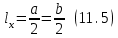 2) 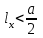 ; скобка (11.4)>0. ; скобка (11.4)>0. 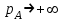 и и 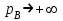  1- теоретическая кривая; 2 - экспериментальная кривая Предельное состояние грунтов оснований фундаментов. 1. Условия наступления предельного напряженного состояния в точке грунтового основания. Предельное напряженное состояние грунта в конкретной точке снования – это такое состояние, при котором наступает необратимый сдвиг одной части грунта относительно другой. Т.е. в данной точке основания наступило окончание II стадии НДС и началась III стадия, когда без дальнейшего увеличения нагрузки продолжается нарастание деформаций. Рассмотрим площадку произвольного наклона в данной точке и напряжения, действующее по этой площадке. Все возможные соотношения между касательной и нормальными напряжениями по закону Кулона можно записать в виде: 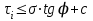 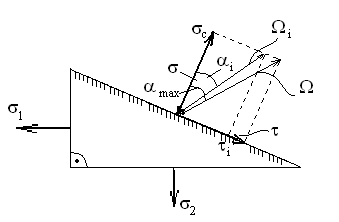 (11.6) (11.6)С увеличением касательных напряжений, они достигают предельных значений, величину которых обозначим 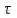 . Тогда условие наступления предельного напряженного состояния будет записываться законом кулона: . Тогда условие наступления предельного напряженного состояния будет записываться законом кулона: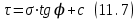 Введем понятие «фиктивное» нормальное напряжение эквивалентное сцеплению грунта и обозначим его: σс - нормальный эквивалент сцепления. 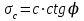 (11.8) (11.8)φ – угол внутреннего трения. σс- это те касательные напряжения, которые нужно приложить для сдвига грунта, когда сопротивление сдвигу обусловлено только силами сцепления. Выразим из (11.8) величину сцепления и подставим в формулу (11.7): 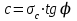 (11.9) (11.9)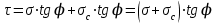 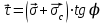 (11.10) (11.10)Предполагая 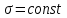 и увеличивая и увеличивая 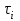 до до 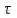 , получаем векторную диаграмму. , получаем векторную диаграмму.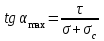 из из 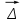 (11.11) (11.11)Из (11.10) 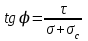 (11.12) (11.12)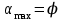 (11.13) (11.13) 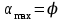 (11.14) (11.14)Рассмотрим 2 главные площадки, по которым действуют главные напряжения σ1 и σ2. Рассматривая диаграмму Мора для прямой задачи получим условия наступления ПНС. σ1>σ2 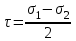 (12.1) (12.1)σ, τ → по площадке произвольного наклона τ ≠σ 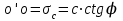 (12.2) (12.2) (12.3) (12.3)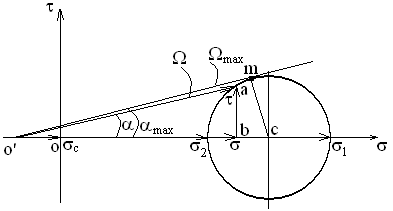 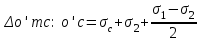 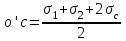 (12.4) (12.4)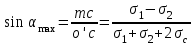 (12.5) (12.5)Используя условие наступления НПС (11.14) и подставляя в левую часть уравнения (12.5) угол внутреннего трения 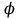 , получаем условие наступления ПНС через главные напряжения. , получаем условие наступления ПНС через главные напряжения.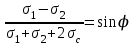 (12.6) (12.6)при  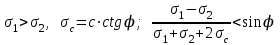 (12.7) (12.7)Условие (12.6) используется для расчета грунтовых оснований на прочность. Представления о форме и размерах областей ПНС Рассмотрим основание жесткого фундамента при различных нагрузках, соотношениях глубины заложения и ширины подошвы. 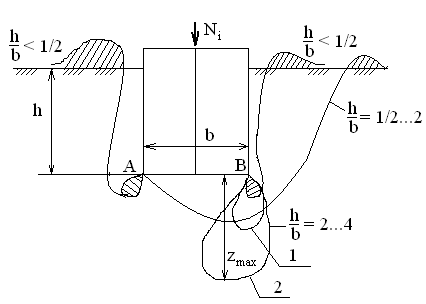 В краевых точках при определенных нагрузках будут зарождаться области ПНС. Форма и размеры областей зависит от соотношения h/b. I область 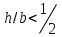 II область 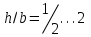 III область 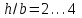 N2 > N1 Интересует 3 главных вопроса при оценке НПС: 1) при каких нагрузках N и давлениях по подошве p зарождаются в краевых точках области ПНС? 2) если давление достигло значения, при котором область ПНС появляется, то какова максимальная глубина, на которую эта область распространяется? 3) при каком давлении по подошве полностью исчерпывается прочность основания? 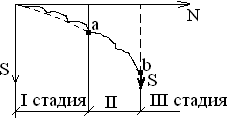 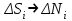 (12.8) (12.8) I – линейных деформаций. II – пластич. деформаций. III – быстро протекающая ползучесть. Значение давления, при котором область ПНС развив-ся на zmax называется критическим давлением, если pкрит таково, что деформация находится в I стадии, то такие давления и такие zmax позволяют в расчетах применять расчетную модель линейно-деформированного основания в пределах отрезка о-а. В дальнейшем области ПНС становятся такими большими, что зависимость между деформациями S и нагрузкой N перестает быть линейной. По т.а и соотв. pкрит рассчитывают допускаемые давления по подошве фундамента. В соответствии со СНиП 2.02.01 – 83 это допускаемое давление называется расчетным давлением R, МПа. 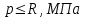 (12.9) (12.9)3. Определение критических давлений по подошве сооружения. Рассмотрим жесткий ленточный фундамент и давления по подошве от внешних нагрузок и собственного веса груза. Обозначим p0 – дополнительное давление на уровне подошвы к природному рб 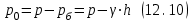 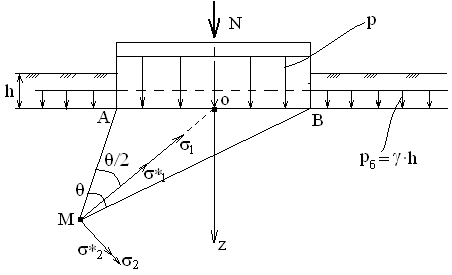 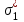 и и 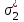 - главные напряжения от дополнительного давления р0. - главные напряжения от дополнительного давления р0.  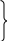 уравнения Митчеля. уравнения Митчеля.Учитывая напряжения от собственного веса в т.М, 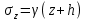 (12.13) и (12.13) и 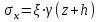 (12.14) (12.14)получаем полные значения напряжений, при этом ввиду параллельности 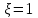 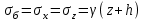 (12.15) (12.15)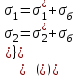 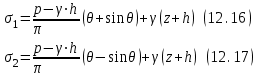 Подставляем σ1 и σ2 в формулу (12.6) и получаем формулы для определения zmax и ркрит, при котором эта глубина равна: 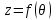 . .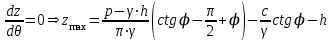 (12.18) (12.18)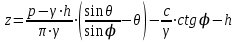 (12.19) (12.19)если zmax > 0, то p = pкр Давление называется критическим, если в основании сооружения образуются области ПНС с определенными размерами и глубиной распределения zmax. 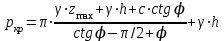 (12.21) (12.21) 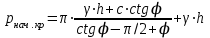 (12.22) (12.22)Начальное критическое давление – это характеристика основания, численно равная значению среднего давления по подошве, при котором в кривых точках зарождаются области ПНС. 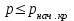  (12.23) – условие, при котором не будет областей ПНС. (12.23) – условие, при котором не будет областей ПНС.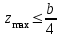 (12.24) (12.24)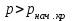 - условие, при котором будут области ПНС. - условие, при котором будут области ПНС.Расчетные сопротивления грунта в подошве жестких фундаментов. Из (12.21) допуская развитие областей ПНС до величины 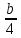 , учитывая коэффициенты предельного состояния, получаем значения критического давления, которое называется расчетным сопротивлением грунта по подошве фундамента. , учитывая коэффициенты предельного состояния, получаем значения критического давления, которое называется расчетным сопротивлением грунта по подошве фундамента. γ- удельный вес грунта ниже подошвы. |
