Определение и сущность железобетона. Определение и сущность железобетон. Литература Филиппов П. П. Как внешние сигналы передаются внутрь клетки
 Скачать 0.88 Mb.
|
Общие сведения. При расчёте прочности железобетонных конструкций выделяют два типа задач:С ОДИНОЧНОЙ АРМАТУРОЙ РАСЧЕТ ИЗГИБАЕМЫХ ЭЛЕМЕНТОВ ТАВРОВОГО СЕЧЕНИЯ ЛЕКЦИЯ 8 Прямоугольного сечения При расчёте прочности железобетонных конструкций выделяют два типа задач: I тип – проверка прочности, заданного сечения элемента. II тип – расчёт сечений: а) подбор арматуры при известных размерах сечения элемента под заданный силовой фактор; б) определение размеров поперечного сечения элемента и арматуры в нём под заданный силовой фактор. 1. Общие сведения 2. Расчёт изгибаемых элементов таврового сечения с полкой в растянутой зоне 3. Расчёт изгибаемых элементов таврового сечения с полкой в сжатой зоне Тавровые сечения встречаются в практике строительства в виде отдельных элементов - балок, а так же в составе конструкций - в монолитных ребристых и сборных панельных перекрытиях. Тавровое сечение состоит из полки – горизонтального и ребра – вертикального элементов. Полка может находиться в сжатой или растянутой зонах (рис. 8а, 8б). Несущая способность железобетонного элемента не зависит от площади сечения бетона растянутой зоны. Поэтому в сравнении с прямоугольным сечением тавровое сечение значительно выгоднее, т.к. при одной и той же несущей способности бетона расходуется меньше вследствие сокращения размеров растянутой зоны. По той же причине тавровое сечение с полкой в сжатой зоне более целесообразно т.к. полка в растянутой зоне не повышает несущей способности элемента. а) б) 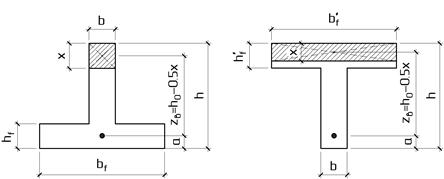 Рисунок 8.1 – Тавровые сечения в отдельных балках: а – балка с полкой в растянутой зоне; б – балка с полкой в сжатой зоне а) 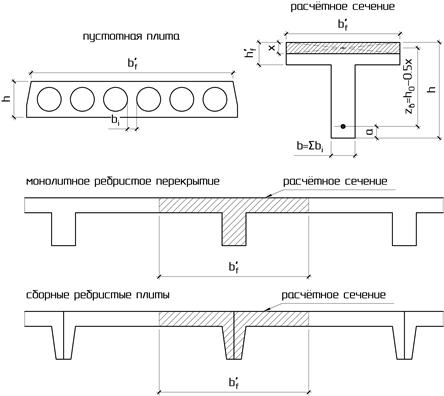 б) в) Рисунок 8.2 – Тавровые сечения в составе перекрытий а – тавровое сечение пустотной плиты;б – тавровое сечение в составе монолитного ребристого перекрытия; в – тавровое сечение в составе сборного перекрытия 2. Расчёт изгибаемых элементов таврового сечения С полкой в сжатой зонеС полкой в растянутой зоне 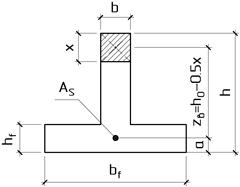 Рисунок 8.3 – К расчёту тавровых сечений с полкой в растянутой зоне В данном случае полка находится в растянутой зоне. Растянутый бетон в расчёте не учитывают, так как в нём имеются трещины. Поэтому расчёт прочности таких элементов выполняют как прямоугольных сечений с размерами . 3. Расчёт изгибаемых элементов таврового сечения При расчётеизгибаемых элементов таврового сечения с полкой в сжатой зоне в зависимости от положения нейтральной оси возможны два случая расчёта: - нейтральная ось находится в пределах полки (1 случай); - нейтральная ось находится в пределах ребра > (2 случай). 1) Определение случая расчёта 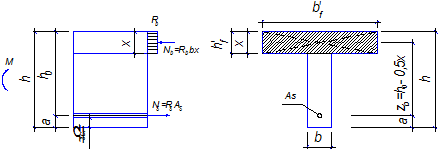 Рисунок 8.4 – Схема усилий при определении случая расчёта изгибаемых элементов таврового сечения Предположим, что нейтральная ось проходит по низу полки, т.е. вся полка сжата и тогда . Равнодействующие нормальных напряжений в сжатом бетоне и в растянутой арматуре равны:  , .Плечо внутренней пары сил  .Рассмотрим равновесие элемента (рис. 15) под действием изгибающего момента от нагрузки и внутренних усилий, возникающих в сжатом бетоне и растянутой арматуре . 1. ; ; ;  .Если  , то , т.е. нейтральная ось находится в пределах полки и будем иметь 1 случай расчёта тавровых сечений.Если > , то > , т.е. нейтральная ось находится в пределах ребра и будем иметь 2 случай расчёта тавровых сечений. Данные уравнения применяют для определения случай расчёта тавровых сечений при решении I типа задач – проверки прочности, заданного сечения элемента. 2. ;  ; ;  .Выражение  представляет собой изгибающий момент, воспринимаемый сжатой полкой.Если  , то , т.е. нейтральная ось находится в пределах полки и будем иметь 1 случай расчёта тавровых сечений.Если >  , то > , т.е. нейтральная ось находится в пределах ребра и будем иметь 2 случай расчёта тавровых сечений.Данные уравнения применяют для определения случай расчёта тавровых сечений при решении II типа задач – расчёта сечений элемента. 2) Расчёт прочности изгибаемых элементов таврового сечения по I случаю расчёта 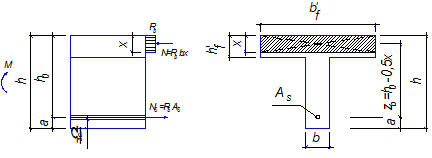 Рисунок 8.5 – Схема усилий по I случаю расчёта прочности изгибаемых элементов таврового сечения Предположим, что выполняются следующие условия:  и ,тогда нейтральная ось находится в пределах полки, и имеем I случай расчёта. Так как растянутый бетон в расчёте не учитывают, по причине наличия в нём трещин, то расчёт прочности тавровых сечений со сжатой зоной в пределах полки выполняют аналогично расчёту прямоугольных сечений с размерами . В расчётных формулах вместо ширины сечения подставляют ширину полки (кроме формулы для определения минимальной площади арматуры):          3) Расчёт прочности изгибаемых элементов таврового сечения по II случаю расчёта 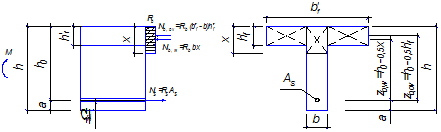 Рисунок 8.6 – Схема усилий по II случаю расчёта прочности изгибаемых элементов таврового сечения Предположим, что выполняются следующие условия: > и >  ,тогда > нейтральная ось находится в пределах ребра, и имеем II случай расчёта. Условно разделим площадь сжатой зоны бетона на две части: площадь бетона сжатого ребра и площадь бетона сжатых свесов  .Предельное усилие, воспринимаемое сжатым бетоном , определим как сумму усилий, которые воспринимают сжатый бетон ребра  и сжатый бетон свесов  .Плечи пар сил (расстояния от центра тяжести сечения арматуры до точек приложения каждого из усилий) в соответствие с рис. 8.6 равны и  Рассмотрим равновесие элемента (рис. 16) под действием изгибающего момента от нагрузки М и внутренних усилий, возникающих в сжатом бетоне и , и растянутой арматуре . 1. ;  ;  ; .Высота сжатой зоны бетона ребра равна 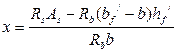 .Площадь сечения растянутой арматуры 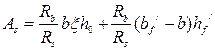 , подставив в формулу , получим .2. ;  ;  ; .Выражение  представляет собой предельный изгибающий момент, воспринимаемый данным сечением, который называют несущей способность сечения.Тогда условие прочности изгибаемого элемента таврового сечения на действие изгибающего момента примет вид  .Выполнив подстановку , получим  = .Обозначив  , получим условие прочности изгибаемого элемента таврового сечения в другом виде .Приравняв внешний и внутренний моменты , можно определить коэффициенты 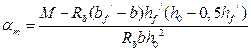 и .Приведённые выше формулы справедливы при условии или , т.е. когда разрушение элемента происходит по растянутой зоне. Если разрушение элемента происходит по сжатой зоне, т.е. > или > , то максимальный предельный изгибающий момент, воспринимаемый тавровым сечением, определяют исходя из значения граничной высоты сжатой зоны бетона , которой соответствуют величины , ,  , тогда и . |