Определение и сущность железобетона. Определение и сущность железобетон. Литература Филиппов П. П. Как внешние сигналы передаются внутрь клетки

• Название: Литература Филиппов П. П. Как внешние сигналы передаются внутрь клетки
• Анкор: Определение и сущность железобетона
• Дата: 14.03.2023
• Размер: 0.88 Mb.
• Имя файла: Определение и сущность железобетон.docx
• Тип: Литература; #987540
• страница: 20 из 20

Разрушение от действия изгибающего момента

Общие положения

ПО СЕЧЕНИЯМ НАКЛОННЫМ К ПРОДОЛЬНОЙ ОСИ ЭЛЕМЕНТА

РАСЧЕТ ИЗГИБАЕМЫХ ЭЛЕМЕНТОВ НА ПОЧНОСТЬ

ЛЕКЦИЯ 9

1. Общие положения

2. Расчёт изгибаемых элементов по сжатой бетонной полосе между наклонными сечениями

3. Расчёт изгибаемых элементов по наклонным сечениями на действие поперечных сил (расчёт поперечной арматуры)

4. Расчёт изгибаемых элементов по наклонным сечениями на действие изгибающих моментов

5. Конструктивные требования к постановке поперечной арматуры

Возможны три типа разрушения изгибаемых элементов по наклонным сечениям:

Причина разрушения – недостаток продольной рабочей арматуры или её недостаточная анкеровка за опору. Напряжения в продольной арматуре достигают предела текучести или она продёргивается в толще бетона. Происходит поворот двух частей элемента вокруг шарнира, образовавшегося в сжатой зоне в конце наклонной трещины, и раздробление сжатого бетона (рис. 9.1).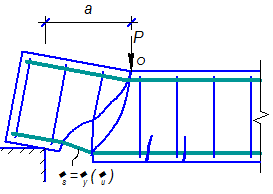



Рисунок 9.1 – Схема разрушения изгибаемых элементов по наклонным сечениям от действия изгибающего момента;

Разрушение бетонной полосы между наклонными трещинами

Разрушение от действия поперечной силы.

Причина разрушения – недостаток поперечной арматуры в зоне действия максимальной поперечной силы. Напряжения в поперечной арматуре достигают предела текучести и происходит одновременно срез двух частей элемента по наклонной трещине и раздробление сжатого бетона (рис. 9.2).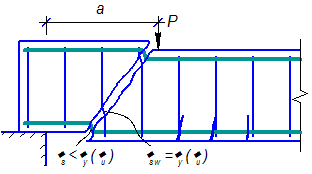



Рисунок 9.2 – Схема разрушения изгибаемых элементов по наклонным сечениям от действия поперечной силы;

Причина разрушения – совместное действие в двух взаимно-перпендикулярных направлениях главных сжимающих и растягивающих напряжений. Происходит разрушение бетона, который находится в сложном напряжённом состоянии – двухосном сжатии-растяжении (рис. 9.3).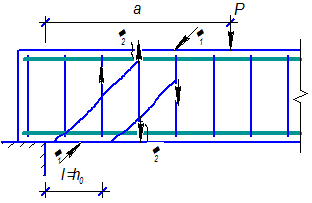



Рисунок 9.3 – Схема разрушения изгибаемых элементов по бетонной полосе между трещинами от совместного действия сжимающих (σ₁) и растягивающих (σ₂) напряжений.

Сущность расчёта изгибаемых элементов по наклонным сечениям заключается в проверке прочности сжатой бетонной полосы между наклонными трещинами и прочности наклонных сечениё на действие поперечной силы, а так же изгибающего момента.

2. Расчёт изгибаемых элементов по сжатой бетонной полосе между наклонными сечениями

Расчёт производят из условия

,

где  – поперечная сила в нормальном сечении, принимаемая на расстоянии от опоры не менее  ;

= 0,3 для тяжёлого бетона.

Если  , то необходимо повысить класс бетона или (и) размеры поперечного сечения балки, в первую очередь ширину сечения  .

3. Расчёт изгибаемых элементов по наклонным сечениям на
действие поперечных сил (расчёт поперечной арматуры)

Расчёт поперечной арматуры необходим, если выполняется условие  ,

где  для тяжёлого бетона.

Если 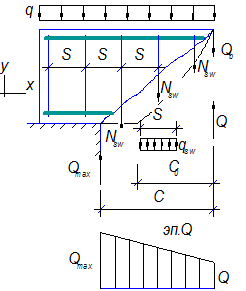 , то расчёт поперечной арматуры не нужен, и тогда её устанавливают по конструктивным требованиям.



Рисунок 9.4 – Схема усилий в наклонном сечении при расчёте его на действие поперечной силы

Рассмотрим равновесие элемента (рис. 3) и спроецируем действующие усилия на вертикальную ось.

, (*)

,

где  - поперечная сила в конце наклонного сечения с длиной проекции с на продольную ось элементаот внешней нагрузки;

– поперечная сила, воспринимаемая бетоном в наклонном сечении;

- поперечная сила, воспринимаемая поперечными стержнями в наклонном сечении.

Подставив Q, Q_b, Q_sw в исходное уравнение (*) получим условие прочности изгибаемого элемента по наклонному сечению на действие поперечной силы

.

– момент силы, воспринимаемой бетоном, относительно начала наклонного сечения, который принимают равным  ( = 1,5 для тяжёлого бетона). Тогда  .

Значение поперечной силы, воспринимаемой бетоном в наклонном сечении принимают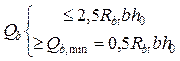

.



Где  = 0,75 для тяжёлого бетона;

- поперечное усилие в стержнях на единицу длины элемента;

S – шаг поперечных стержней вдоль элемента.

с₀ – длина проекции наклонной трещины на продольную ось элемента, принимаемая равной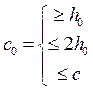

.

Преобразуем исходное выражение (*)

,

где  и  ,

тогда

.

Продифференцируем данное выражение по  при  , что соответствует минимальному значению несущей способности элемента по поперечной силе:  .

Тогда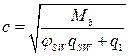

≤  ,

где: , если действует сплошная равномерно распределённая нагрузка  ;

, если нагрузка  включает в себя временную нагрузку  .

При действии на элемент сосредоточенных сил значение  принимают равным расстояниям от опоры до точек приложения этих сил, а так же равным 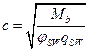 , но не меньше  , если это значение меньше расстояния от опоры до 1-го груза.

Если 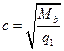 , следует принимать  .

Поперечную арматуру учитывают в расчёте, если соблюдается условие  .

При расчёте поперечной арматуры обычно задаются диаметром поперечных стержней  и их шагом  вдоль элемента по конструктивным требованиям, вычисляют   и  , и проверяют условие прочности изгибаемого элемента по наклонному сечению на действие поперечной силы
.

При этом шаг поперечных стержней, учитываемых в расчёте, должен быть не более  .

В случае не обеспечения по расчёту прочности наклонного сечения при первоначально принятых исходных данных (шаг поперечных стержней  , диаметр поперечных стержней  ), требуется увеличить диаметр поперечных стержней или (и) уменьшить их шаг и повторно выполнить проверочный расчёт.

4. Расчёт изгибаемых элементов по наклонным

Сечениями на действие изгибающих моментов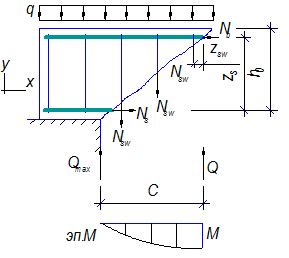

Рисунок 9.5 – Схема усилий в наклонном сечении при расчёте его на действие изгибающего момента

Рассмотрим равновесие элемента (рис. 9.5) и составим уравнение моментов действующих усилий относительно точки приложения равнодействующей напряжений в сжатом бетоне  .

, (**)

,

где  - момент в наклонном сечении с длиной проекции  на продольную ось элемента от внешней нагрузки;

- момент, воспринимаемый продольной арматурой, пересекающей наклонное сечение;

- момент, воспринимаемый поперечной арматурой, пересекающей наклонное сечение.

Подставив М, М_S, M_SW в исходное уравнение (**) получим условие прочности изгибаемого элемента по наклонному сечению на действие изгибающего момента

.

;

.

- проинтегрируем данное выражение по переменной  .

,

где  , тогда  .

Интегрируя, получим  ,

где  ,

Величину  принимают из условия, что поперечная сила в наклонном сечении воспринимается только поперечными стержнями, т.е.  , отсюда выразим  .

При действии на элемент сосредоточенных сил значение  принимают равным расстояниям от опоры до точек приложения этих сил, а так же равным  , но не меньше  , если это значение меньше расстояния от опоры до 1-го груза.

Расчёт на действие момента производят для наклонных сечений, расположенных:

- у грани крайней свободной опоры элементов;

- в местах обрыва продольной арматуры в пролёте;

- в местах резкого изменения высоты элемента;

- у свободного края консолей.

Несущая способность наклонного сечения по изгибающему моменту не должна быть ниже несущей способности нормального сечения, проходящего через эту точку. При достаточной анкеровке продольной рабочей арматуры на крайних опорах и в пролётах это требование будет выполняться, и тогда расчёт наклонных сечений по изгибающему моменту можно не производить:

1. При отсутствии наклонных трещин, т.е. при соблюдении условия  , растянутые стержни должны быть заведены за внутреннею грань свободной опоры на длину анкеровки  .

2. Если  , т.е. при наличии наклонных трещин, длина запуска арматуры за грань опоры должна быть  и не менее 200 мм. Для стержней диаметром менее 36 мм значение коэффициента = 15 – 93 принимают по таблице норм в зависимости от классов бетона и арматуры и коэффициента ά, учитывающего влияние поперечного обжатия бетона и поперечной арматуры.

3. Обрываемые в пролёте стержни должны заводиться за точку теоретического обрыва, т.е. за нормальное сечение, в котором внешний момент становится равным предельному моменту без учёта обрываемой арматуры (рис. 23), на длину ,

где  - поперечная сила в нормальном сечении, проходящем через точку теоретического обрыва.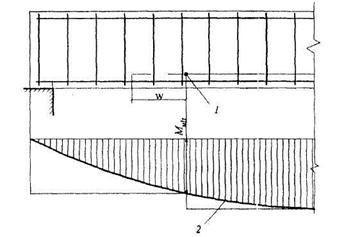



Рисунок 9.6 – Обрыв растянутых стержней в пролете

1- точка теоретического обрыва; 2- эпюра М

Поперечной арматуры

Конструктивные требования к постановке

Диаметр поперечных стержней в сварных каркасах из условия доброкачественной сварки следует принимать не менее 0,25 от наибольшего диаметра продольной арматуры -  . Диаметр поперечных стержней в вязаных каркасах принимают не менее 6 мм.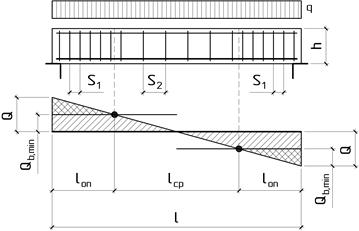



Рисунок 9.7 – К определению длин приопорных участков графическим способом при равномерно распределённой нагрузке.

На приопорных участках пролётов изгибаемых элементов, где поперечная сила по расчёту не может быть воспринята только бетоном, шаг поперечных стержней  принимают:  .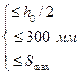

На средних участках пролётов изгибаемых элементов, где поперечная сила по расчёту воспринимается только бетоном, шаг поперечных стержней  принимают:  .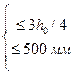

Поперечную арматуру можно не устанавливать в сплошных и многопустотных плитах при h < 300 мм и в балках при h < 150 мм, если поперечная арматура по расчёту не требуется.

Расчётную длину приопорных участков , на которых следует размещать поперечные стержни с учащённым шагом  , принимают большую из двух величин, определённых теоретическим и графическим способом (рис. 9.7). Фактическую длину приопорных участков устанавливают при конструировании каркасов при разбивке шагов их поперечных стержней, которая должна быть не менее расчётной длины.

При действии на элемент сосредоточенных сил расчётную длину приопорных участков  принимают равной расстоянию от опоры до ближайшей силы или до точки приложения силы, после которой поперечная арматура по расчёту не нужна.