Статистика синергия. Статистика. Литература по теме Практические задания
 Скачать 1.83 Mb. Скачать 1.83 Mb.
|
|
Тема 5. Статистические показатели. Показатели в форме средних величин Цель изучения темы состоит в формировании системы знаний о категории и видах средних величин, овладении методами расчета и интерпретации статистических показателей, выраженных средними величинами. В результате успешного освоения темы Вы: Узнаете: · что такое средняя величина и для чего она применяется; · что такое логическая формула средней величины; · какие виды средних величин существуют и как они рассчитываются; · что такое структурные средние и что они характеризуют; · как рассчитываются структурные средние. Приобретете компетенции: · владение методами теоретического и экспериментального исследования; · понимание роли и значения информации в развитии современного общества и экономических знаний; · владение основными методами, способами и средствами получения, хранения, переработки информации; · способность оценивать воздействие макроэкономической среды на функционирование организаций; · способность анализировать финансовую отчетность и принимать обоснованные решения; · способность оценивать эффективность использования различных систем учета и распределения затрат, иметь навыки калькулирования и анализа себестоимости продукции; · способность обосновывать решения в сфере управления оборотным капиталом; · умение обоснованно выбирать вид средней величины в зависимости от особенностей исходной числовой информации; · владение методами расчета и анализа статистических показателей в форме средних величин и формулирования обоснованных выводов на основе рассчитанных значений. В процессе освоения темы акцентируйте внимание на следующих ключевых понятиях: · средняя величина; · определяющее свойство средней величины; · исходное соотношение средней величины (ИСС); · средняя арифметическая простая; · средняя арифметическая взвешенная; · средняя гармоническая взвешенная; · средняя геометрическая; · средняя квадратическая; · средняя хронологическая; · мода; · медиана. Вопросы темы: 1. Сущность и исходное соотношение средней величины. 2. Средняя арифметическая и ее свойства. 3. Средняя гармоническая, квадратическая и геометрическая. 4. Средняя хронологическая. 5. Структурные средние. Теоретический материал по теме Вопрос 1. Сущность и исходное соотношение средней величины. Наиболее распространенной формой статистических показателей, используемой в экономических исследованиях, является средняя величина. Средняя величина представляет собой обобщенную количественную характеристику признака в статистической совокупности в конкретных условиях места и времени. Важнейшее свойство средней величины заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности. Значения признака отдельных единиц совокупности колеблются под влиянием множества факторов, среди которых могут быть как основные, так и случайные. Например, курс акций корпорации в основном определяется финансовыми результатами ее деятельности. В то же время в отдельные дни и на отдельных биржах эти акции в силу обстоятельств могут продаваться по более высокому или заниженному курсу. В средней взаимопогашаются случайные отклонения, и учитываются изменения, вызванные действием основных факторов. Это позволяет средней отражать типичный уровень признака, независимо от индивидуальных особенностей отдельных единиц. Категорию средней можно раскрыть через понятие определяющего свойства. Согласно этому понятию средняя, являясь обобщающей характеристикой всей совокупности, ориентируется на определенную величину, связанную со всеми единицами изучаемой совокупности. Эту величину можно представить в виде функции: f (х1, х2, ..., хn) (12) Если в функции (12) все величины х1, х2, ... , хn заменить их средней величиной , то значение этой функции должно остаться прежним: На практике среднюю можно определить через исходное соотношение средней (ИСС) или ее логическую формулу: Для каждого показателя, используемого в экономическом анализе, можно составить только одно истинное исходное соотношение для расчета средней. Например, для расчета средней заработной платы работников предприятия необходимо общий фонд заработной платы разделить на число работников: Средний размер одного вклада в банк определяется как: Вопрос 2. Средняя арифметическая и ее свойства. Чаще других на практике используется средняя арифметическая, которая, как и все средние, может быть простой или взвешенной. Средняя арифметическая простая используется в тех случаях, когда расчет осуществляется по несгруппированным данным. Предположим, шесть торговых предприятий фирмы имеют следующий объем товарооборота за месяц:
Среднемесячный товарооборот в расчете на одно предприятие определяет следующее исходное соотношение: Используя условные обозначения, запишем формулу средней арифметической простой: Подставив в формулу данные, рассчитаем среднюю: Средняя арифметическая взвешенная используется, когда все или отдельные значения осредняемого признака повторяются, т.е. для расчета средней величины по сгруппированным данным или рядам распределения. Рассмотрим следующий условный пример. Таблица 19. Сделки по акциям эмитента «ХХХ» за торговую сессию
Определим по данному дискретному вариационному ряду средний курс продажи 1 акции, что можно сделать, используя исходное соотношение: Чтобы получить общую сумму сделок, необходимо по каждой сделке курс продажи (Хi) умножить на количество проданных акций (fi) и полученные произведения сложить: Расчет среднего курса продажи произведен по формуле средней арифметической взвешенной: 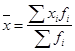 (15) (15)В отдельных случаях веса могут быть представлены не абсолютными величинами, а относительными (в процентах или долях единицы). Если для расчета средней по данным табл. 19 использовать удельные веса, преобразовав формулу (15), получим: 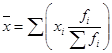 (16) (16)Или можно выразить удельный вес в долях единицы: При расчете средней по интервальному вариационному ряду от интервалов переходят к их серединам. При этом ширина открытых интервалов (первого и последнего) условно приравнивается к ширине интервалов, примыкающих к ним (второго и предпоследнего). Рассмотрим следующий пример (табл. 20). Таблица 20. Распределение сотрудников предприятия по возрасту
Для определения среднего возраста персонала найдем середины возрастных интервалов: 22,5 (для интервала до 25), 27,5 (для интервала 25–30), 35,0 (для интервала 30–40), 45,0 (для интервала 40–50), 55,0 (для интервала 50–60), 65,0 (для интервала 60 и более). Используя среднюю арифметическую взвешенную, определим средний возраст работников данного предприятия: На практике наиболее часто встречаемая при расчете средних ошибка заключается в игнорировании весов. Например, имеются следующие данные: Таблица 21. Себестоимость продукции «Z»
Можно ли по имеющимся данным определить среднюю себестоимость единицы продукции по двум предприятиям вместе? Можно, но только в том случае, когда объемы производства данной продукции на двух предприятиях совпадают. Тогда средняя себестоимость составит 38,0 руб. ((37 + 39) : 2). Однако если на первом предприятии произведено 50 единиц продукции, а на втором – 700, для расчета средней себестоимости потребуется уже средняя арифметическая взвешенная: Вывод: использовать среднюю арифметическую невзвешенную можно только тогда, когда точно установлено отсутствие весов или их равенство. Средняя арифметическая обладает математическими свойствами, которые более полно раскрывают ее сущность и в ряде случаев используются для ее расчета. Рассмотрим эти свойства. 1.Произведение средней на сумму частот равно сумме произведений отдельных вариантов на соответствующие им частоты: Проверим свойство на примере расчета среднего курса продажи акций (табл. 19). За счет округления среднего курса правая и левая части равенства в данном случае будут несколько отличаться: 417,03 ´ 1 850 = 420 ´ 700 + 440 ´ 200 + 410 ´ 950 2.Сумма отклонений индивидуальных значений признака от средней арифметической равна нулю: Для нашего примера: (420 – 417,03) ´ 700 + (440 – 417,03) ´ 200 + (410 – 417,03) ´ 950 0 3.Сумма квадратов отклонений индивидуальных значений признака от средней арифметической меньше, чем сумма квадратов их отклонений от любой другой произвольной величины С. Рассмотрим это свойство на упрощенном примере по ряду данных xi = 3, 4, 5. Средняя величина для данного ряда равна 4. Рассчитаем сумму квадратов отклонений от = 4 и от величины С, приняв ее за вариант xi = 3:
Каким бы большим или малым мы ни брали число С, сумма квадратов отклонений индивидуальных значений признака от нее всегда будет больше суммы квадратов их отклонений от средней на величину: 4.Если все осредняемые варианты уменьшить или увеличить на постоянное число А, то средняя арифметическая соответственно уменьшится или увеличится на ту же величину А: 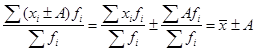 (20) (20)Так, если все курсы продажи акций увеличить на 15 руб., то средний курс также увеличится на 15 руб.: 5.Если все варианты значений признака уменьшить или увеличить в А раз, то средняя также соответственно увеличится или уменьшится в А раз: 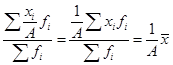 (21) (21)Предположим, курс продажи в каждом случае вырос в 2 раза. Тогда и средний курс также увеличится на 100 %: 6.Если все веса уменьшить или увеличить в А раз, то средняя арифметическая от этого не изменится: 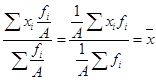 (22) (22)Так, в нашем примере удобнее было бы рассчитывать среднюю, предварительно поделив все веса на 100: Вопрос 3. Средняя гармоническая, квадратическая и геометрическая. Средняя гармоническая взвешенная используется, когда известен числитель исходного соотношения средней, но неизвестен его знаменатель. Другими словами, когда в исходных данных нам известны индивидуальные усредняемые значения хi, но нет прямой информации о количестве объектов, т.е. о частотах fi, однако эти данные можно получить при помощи простых расчетов. Например, известна цена 1 кг товара – 50 руб. и общий объем его реализации – 250 руб. Прямого указания на количество реализованных килограмм товара нет, но, разделив 250 на 50, мы легко узнаем, что всего было продано 5 кг. Рассмотрим расчет средней гармонической взвешенной на примере данных таблицы 22. Таблица 22. Реализация товара на трех рынках города за II квартал 2012 г.
Средняя цена любого товара может быть определена только на основе следующего исходного соотношения: Общую выручку легко получить простым суммированием выручек по трем рынкам. Данные же о количестве реализованного товара в кг отсутствуют, но их можно узнать, разделив размер выручки от реализации каждого рынка на цену товара. Определим искомую среднюю: 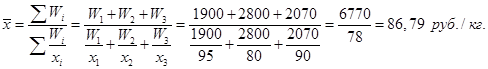 Таким образом, всего было реализовано 78 кг товара, а средняя цена реализации за II квартал 2012 г. составила 86 руб. 79 коп. за 1 кг. В данном случае расчет произведен по формуле средней гармонической взвешенной (23) , где Wi – выручка от реализации, представляющая собой произведение цены товара (хi, руб.) на объем его реализации (fi, кг.) 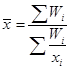 , (23) , (23)где Средняя геометрическая рассчитывается по формулам: Наиболее широкое применение этот вид средней получил в анализе динамики для определения среднего темпа роста, что будет рассмотрено в соответствующей теме. Средняя квадратическая. В основе вычислений ряда сводных расчетных показателей лежит средняя квадратическая: 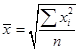 – невзвешенная (26) – невзвешенная (26)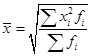 – взвешенная (27) – взвешенная (27)Данный вид средней используется при расчете показателей вариации. Вопрос 4. Средняя хронологическая. Средний уровень моментного ряда динамики рассчитывается по формулесредней хронологической. Для моментного равноотстоящего ряда динамики при расчете среднего уровня используют формулу средней хронологической простой: 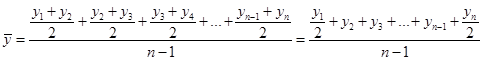 (28) (28)или 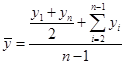 Например, требуется найти среднесписочную месячную численность работников предприятия по данным об их численности на 1-е число каждого месяца в первом квартале 2013 г. (чел.):
Это моментный ряд с равноотстоящими уровнями, поэтому среднемесячная численность работников фирмы за первый квартал 2013 года составила: 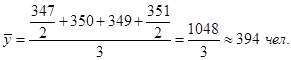 Средний уровень моментных рядов динамики с неравноотстоящими уровнями определяется по формуле средней хронологической взвешенной: 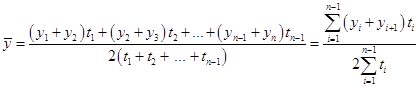 (29) (29)где t – продолжительность интервала времени между соседними уровнями. Например, известна списочная численность рабочих организации на некоторые даты 2012 г. (чел.). Ряд динамики имеет неравноотстоящие уровни во времени:
Среднегодовая численность работников за 2012 г. (по формуле 29) составит: Вопрос 5. Структурные средние. Наиболее часто используемыми в экономической практике структурными средними являются мода и медиана. Мода (Мо) представляет собой значение признака, повторяющееся с наибольшей частотой. Медианой (Ме) называется значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности. Рассмотрим определение моды и медианы по несгруппированным данным. Предположим, что 9 торговых фирм города реализуют товар А по следующим оптовым ценам (тыс. руб.). 4,4 4,3 4,4 4,5 4,3 4,3 4,6 4,2 4,6 Так как чаще всего встречается цена 4,3 тыс. руб., то она и будет модальной. Для определения медианы необходимо провести ранжирование: 4,2 4,3 4,3 4,3 4,4 4,4 4,5 4,6 4,6 Центральной в этом ряду является цена 4,4 тыс. руб., следовательно, она и будет медианой. Если ранжированный ряд включает четное число единиц, то медиана определяется как средняя из двух центральных значений. В отличие от моды, медиана практически выполняет функции средней для неоднородной, не подчиняющейся нормальному закону распределения совокупности. Медиана используется в случаях, когда средняя не позволяет объективно оценить исследуемую совокупность из-за сильного влияния на нее максимальных и минимальных значений. Проиллюстрируем познавательное значение медианы следующим примером. Допустим, нам необходимо дать характеристику среднего дохода группы людей, насчитывающей 100 человек, из которых 99 имеют доходы в интервале от 30 до 60 тыс. руб. в месяц, а месячные доходы последнего составляют 200 тыс. руб.:
Средняя арифметическая покажет средний доход в 120–140 тыс. руб., который не только значительно меньше дохода сотого человека, но и имеет мало общего с доходами основной части группы. Медиана, равная 43 тыс. руб. (= (42 + 44) : 2), позволит дать объективную характеристику уровня доходов 99 % данной группы людей. Рассмотрим расчет Мо и Ме по сгруппированным данным (табл. 23). Таблица 23. Распределение торговых предприятий города по уровню цен на товар А
В дискретных рядах распределения мода – это значение, имеющее наибольшую частоту. Цену 55 руб. установили максимальное число предприятий (60), следовательно, она является модальной. Для определения медианы находят номер медианной единицы ряда: где n – объем совокупности. В нашем случае: Полученное дробное значение, всегда имеющее место при четном числе единиц совокупности, указывает, что точная середина ряда находится между 95 и 96 предприятиями. Необходимо определить, в какой группе находятся предприятия с этими порядковыми номерами. Это можно сделать, по накопленной частоте Si. Очевидно, что магазинов с этими номерами нет в первой группе, где всего лишь 12 торговых предприятий, нет их и во второй группе (12 + 48 = 60). 95 и 96 предприятия находятся в третьей группе (12 + 48 + 56 = 116) и, следовательно, медианой является цена 54 руб. Определение моды и медианы по интервальным рядам требует проведения расчетов на основе следующих формул: 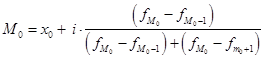 , (31) , (31)где x0 – нижняя граница модального интервала (модальным называется интервал, имеющий наибольшую частоту); i – ширина модального интервала; – частота модального интервала; – частота интервала, предшествующего модальному; – частота интервала, следующего за модальным. 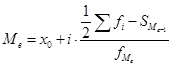 , (32) , (32)где x0 – нижняя граница медианного интервала (медианным называется первый интервал, накопленная частота которого превышает половину общей суммы частот); i – ширина медианного интервала; – частота медианного интервала. Рассчитаем моду и медиану по данным таблицы 24. Таблица 24. Распределение населения региона по уровню денежного дохода
Интервал с границами 2 500–2 600 в данном распределении будет модальным, так как он имеет наибольшую частоту (20,1 %). По формуле (31) определим моду: Для определения медианного интервала необходимо определять накопленную частоту каждого последующего интервала до тех пор, пока она не превысит 1/2 суммы накопленных частот (в нашем случае 50 %):
Медианным является интервал с границами 2 600 – 2 700. Определим медиану по формуле 32: Соотношение моды, медианы и средней арифметической указывает на характер распределения признака в совокупности, позволяет оценить его асимметрию. Если Мо < Me < , имеет место правосторонняя асимметрия, при < Me < Мо следует сделать вывод о левосторонней асимметрии ряда. На основе полученных в последнем примере значений структурных средних можно заключить, что наиболее распространенным, типичным является среднедушевой доход порядка 2 560 руб. в месяц. В то же время более 1/2 населения располагает доходом свыше 2 670 руб. при среднем уровне 2 735 руб. (средняя арифметическая взвешенная). Из соотношения этих показателей следует вывод о правосторонней асимметрии распределения населения по уровню среднедушевых денежных доходов, что позволяет предполагать достаточную емкость рынка дорогих товаров повышенного качества и товаров престижной группы. Вопросы для самопроверки: 1. Что такое средняя величина и каковы ее основные виды? 2. Что представляет собой исходное соотношение средней величины? 3. В каких случаях применяются взвешенные средние величины? Почему при расчете средней величины важно учитывать веса вариантов показателя? 4. Какими математическими свойствами обладает средняя арифметическая величина? 5. В каких случаях применяется средняя гармоническая величина? 6. Какой вид средних величин используется для расчета среднего значения по моментным рядам динамики? 7. Что такое мода и для чего она применяется? 8. Можно ли рассчитать моду по интервальному ряду распределения? 9. Что характеризует медиана? 10. Можно ли вычислить медиану по ряду распределения, не рассчитывая накопленные частоты? Литература по теме: Основная литература: 1. Улитина Е.В. Статистика: учеб. пособие / Е.В. Улитина, О.В. Леднева, О.Л. Жирнова. – 3-е изд. – М.: МФПУ, 2013.– 312 с. – (Университетская серия). Дополнительная литература: 1. Общая теория статистики: статистическая методология в изучении коммерческой деятельности: учебник / Под ред. А.А. Спирина, О.Э. Башиной. – М.: Финансы и статистика, 2004. 2. Практикум по теории статистики: учеб. пособие / Под ред. проф. Р.А. Шмойловой. – М.: Финансы и статистика, 2004. 3. Шмойлова Р.А., Минашкин В.Г., Садовникова Н.А., Шувалова Е.Б. Теория статистики: учебник / Под ред. проф. Р.А. Шмойловой. – М.: Финансы и статистика, 2004. 4. Салин В.Н., Чурилова Э.Ю. Практикум по курсу «Статистика» (в системе STATISTICA). – М.: Социальные отношения, 2006. 5. Методологические положения по статистике. – М.: Госкомстат России, 2010. Практические задания: Задание 1. Распределение рабочих предприятия по тарифному разряду имеет следующий вид:
Определите средний уровень квалификации рабочих предприятия, модальное и медианное значения тарифного разряда. Задание 2. По данным о размере месячного товарооборота сети торговых предприятий определите средний размер месячного товарооборота на одно предприятие, модальное и медианное значения товарооборота.
Задание 3. Производственная деятельность одного из отделений корпорации за месяц характеризуется следующими данными:
Определите средние затраты на 1 руб. произведенной продукции в целом по отделению. Задание 4. По данным об остатках оборотных средств предприятия на начало месяца (тыс. руб.) определите среднемесячный размер остатков оборотных средств за 2012 год.
|
