Статистика синергия. Статистика. Литература по теме Практические задания

• Название: Литература по теме Практические задания
• Анкор: Статистика синергия
• Дата: 16.01.2023
• Размер: 1.83 Mb.
• Имя файла: Статистика.docx
• Тип: Литература; #889718
• страница: 6 из 16

Тема 6. Вариационный анализ финансовых показателей

 

Цель изучения темы состоит в формировании компетенций о системе показателей, используемых для анализа вариации, особенностях методики их расчета, интерпретации и практическом применении.

 

В результате успешного освоения темы Вы:

Узнаете:

·     почему необходимо изучать вариацию;

·     какие показатели вариации существуют и для чего они используются;

·     как рассчитываются и интерпретируются показатели вариации;

·     какими математическими свойствами обладают показатели вариации и как влияет на их величину изменение всех значений данных или перевод в другую шкалу измерений.
Приобретете компетенции:

·     владение методами теоретического и экспериментального исследования;

·     понимание роли и значения информации в развитии современного общества и экономических знаний;

·     владение основными методами, способами и средствами получения, хранения, переработки информации;

·     способность анализировать финансовую отчетность и принимать обоснованные решения;

·     способность оценивать эффективность использования различных систем учета и распределения затрат; иметь навыки калькулирования и анализа себестоимости продукции;

·     способность обосновывать решения в сфере управления оборотным капиталом;

·     умение измерять силу вариации признака при помощи абсолютных и относительных показателей;

·     способность рассчитывать показатели вариации и делать выводы по их значениям;

·     способность оценивать количественную однородность любого набора данных;

·     умение рассчитывать значения показателей вариации при систематическом изменении всех значений исследуемого признака.
В процессе освоения темы акцентируйте внимание на следующих ключевых понятиях:

·     вариация, или изменчивость;

·     отклонение от средней;

·     размах вариации;

·     среднее линейное отклонение;

·     дисперсия;

·     среднее квадратическое отклонение;

·     линейный коэффициент вариации;

·     коэффициент вариации.
Вопросы темы:

1.  Причины изучения вариации.

2.  Показатели вариации и способы их расчета.

3.  Математические свойства показателей вариации.
Теоретический материал по теме
Вопрос 1. Причины изучения вариации.
Одна из причин, по которой существует необходимость в проведении статистического анализа и постоянном сборе и обновлении информации о социальных и экономических явлениях, состоит в том, что данные изменчивы.
Вариацию (от лат. variatio – «изменение, различие»), или изменчивость, можно определить как степень различия между отдельными значениями признака или показателя.
Почему важно изучать вариацию? В чем ценность информации о том, насколько отличаются значения признака друг от друга?

Ситуация, в которой присутствует изменчивость, всегда связана с долей риска и неопределенностью в будущем. Систематическое воздействие различных факторов и условий вызывает изменение отдельных вариантов признаков или показателя в целом. В большинстве случаев обнаружить такое воздействие и тем самым снизить риск возможно, изучая колебания или индивидуальные различия значений, а не обобщающие величины.

Например, биржевой или финансовый аналитик для прогнозирования игры на бирже или анализа поведения конкретной ценной бумаги извлечет больше полезной информации, изучая колебания курса акции, чем среднюю величину курса этой акции. Менеджера по персоналу при изучении производительности труда работников компании будут больше интересовать причина и размер отклонения количества обработанных за день каждым сотрудником заказов от среднего количества заказов, установленного нормой или рассчитанного для данной категории работников. А по тому, насколько мало или велико среднее отклонение от нормы в разных бригадах (отделах, сменах), менеджер сможет судить об их однородности с точки зрения производительности отдельных сотрудников и принять меры для ее выравнивания и повышения в целом по предприятию.

Показатели изменчивости индивидуальных значений используют для организации контроля качества на производстве, оценки доходности финансовых вложений, сравнительном анализе конкурентных возможностей предприятий, планировании затрат, маркетинговых исследованиях, для построения статистических моделей и во многих других случаях.

Каким образом можно получить количественную оценку степени изменчивости (или колеблемости) признака и сделать вывод о степени различия между отдельными его значениями?

Очевидно, что для оценки различия между значениями необходимо сравнить их друг с другом или с некоей постоянной, или объединяющей все эти значения величиной. Согласно определяющему свойству, такой объединяющей все варианты признака величиной является их средняя – или типичный размер признака.

Несмотря на то, что средняя является условным центром распределения вариантов признака, она не дает представления о том, как отдельные значения группируются вокруг нее, сосредоточены ли они вблизи или значительно удалены от центра (рис. 17).
Таблица 25.

Итоги продаж за месяц
№ менеджера	Количество договоров
1	9
2	13
3	15
4	19
5	16
6	20
7	32
8	25
9	17
10	14
Итого	180

 

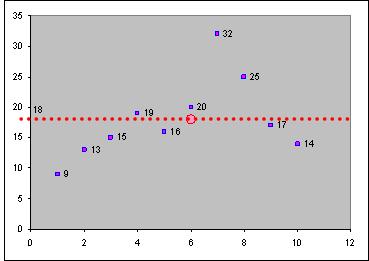Рис. 17. Количество договоров на сервисное обслуживание, заключенных менеджерами по продажам в течение месяца
Примечание.

На графике по оси Х отмечены N менеджеров, а по оси Y – количество заключенных ими договоров (по данным табл. 25). Очевидно, что среднее количество заключенных договоров на одного менеджера составляет 18. Средний уровень продаж отмечен на графике пунктирной линией. Степень удаленности от средней определяется длинной вертикального отрезка от каждой точки на графике, обозначающей количество заключенных соответствующим менеджером договоров, до пунктирной линии.
Чем ближе расположены значения признака к средней, тем, очевидно, больше их близость по отношению друг к другу и тем выше однородность совокупности в целом.

Для количественной характеристики колеблемости признака необходимо оценить расстояние между каждым индивидуальным значением признака и общей для них средней величиной, которое определяется как разность между их значениями. Эту разность в статистике называют отклонением от средней величины (рис. 18.).

 

Таблица 26.

 

Итоги продаж за месяц
№ менеджера	Количество договоров	Отклонение от 18 (от средней величины)
1	9	–9
2	13	–5
3	15	–3
4	19	1
5	16	–2
6	20	2
7	32	14
8	25	7
9	17	–1
10	14	–4
Итого	180	0

 

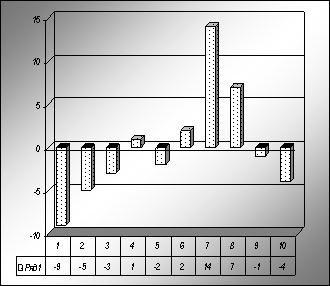Рис. 18. Гистограмма отклонения количества заключенных договоров каждым менеджером от среднего значения, равного 18

 

Вычислив среднее из индивидуальных отклонений, мы узнаем величину типичного стандартного расстояния от средней величины.

Найденное число покажет, насколько в среднем отличается каждое значение признака в данной совокупности от средней величины, и будет служить мерой случайности отклонений отдельных значений.
Вопрос 2. Показатели вариации и способы их расчета.
Для количественного измерения степени близости значений отдельных единиц к средней используется система абсолютных и относительных показателей. В общем виде система показателей вариации представлена на рис. 19.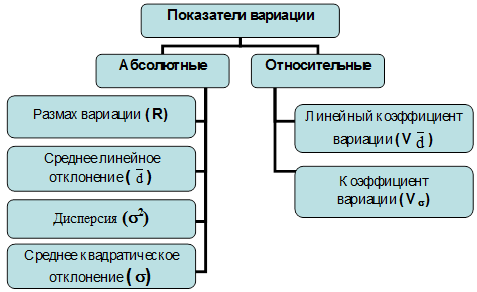

Рис. 19. Основные показатели вариации
Размах вариации – это разность между наибольшим (x_max) и наименьшим (x_min) значениями вариантов.
R = x_max - x_min                           (33)

 

Пример 1. Определим показатель размаха вариации по данным табл. 27.

 

Таблица 27.

 

Группы предприятий по объему товарооборота

 

Товарооборот, млн. руб.	Число предприятий fi
90-100	28
100-110	48
110-120	20
120-130	4
ИТОГО	100

R = 130 - 90 = 40 млн. руб.
Размах показывает, что товарооборот предприятий изменяется (колеблется) в пределах от 90 до 130 млн руб., а общая ширина диапазона принимаемых значений (амплитуда колебаний) составляет 40 млн руб.

Размах измеряется в тех же абсолютных единицах, что и значения признака. Размах устанавливает ширину интервала, занимаемого значениями данных, но не отражает отклонений всех вариантов признака в ряду. Поскольку размах зависит только от крайних значений, его величина в большей мере подвержена воздействию случайности, так как в совокупности аномально большие или маленькие значения данных могут быть получены под влиянием случайных причин.

Чтобы дать обобщающую характеристику распределению отклонений, исчисляют среднее линейное отклонение , которое учитывает различие всех единиц изучаемой совокупности.
Среднее линейное отклонение показывает стандартное отличие значения каждого варианта от общей средней величины и определяется как средняя арифметическая из отклонений индивидуальных значений от средней, без учета их знака (по модулю):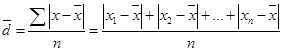

                  (34)

Необходимость использования модуля связана со свойством средней арифметической (см. тему 5), согласно которому сумма индивидуальных отклонений от средней арифметической всегда равна нулю. Среднее линейное отклонение измеряется в тех же абсолютных единицах, что и значения признака.

 

Порядок расчета среднего линейного отклонения:

1)       по значениям признака находят среднюю арифметическую;

2)       определяют отклонения каждого значения x_i от средней ;

3)       рассчитывается сумма абсолютных величин отклонений: ;
4)       сумма абсолютных величин отклонений делится на число значений.
Пример 2. Рассчитаем среднее линейное отклонение стажа работников одной смены по данным табл. 28.

 

Таблица 28.

 

Стаж работников I смены бригады рабочих на предприятии

 

Таб. номер рабочего	Стаж работы, лет ( )
А	1	2	3
3 440	2	- 8	8
3 537	3	- 7	7
3 825	12	2	2
2 171	15	5	5
2 845	18	8	8
Итого	50	0	30

 

Средний стаж работы на одного рабочего смены составляет 10 лет (50 : 5 = 10). Отклонения стажа каждого рабочего от среднего стажа, равного 10 годам, рассчитаны в графе 2, их сумма равна нулю.

Среднее линейное отклонение составляет: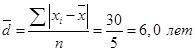
,
т.е. стаж работы каждого работника данной смены в среднем отличается от их среднего значения на 6 лет.
Если данные наблюдения представлены в виде дискретного или интервального ряда распределения с частотами,  исчисляется по формуле средней арифметической взвешенной: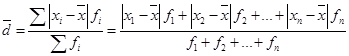

              (35)

Порядок расчета взвешенного среднего линейного отклонения:

1)       вычисляется средняя арифметическая взвешенная;

2)       определяются абсолютные отклонения вариантов от средней ;

3)       полученные отклонения умножаются на частоты ;

4)       находится сумма взвешенных отклонений без учета знака: ;

5)       сумма взвешенных отклонений делится на сумму частот: .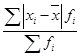
Для нахождения  по интервальному ряду распределения вначале находят середины каждого интервала (как среднюю арифметическую из значений границ) и используют их для расчета отклонений от общей средней аналогичным образом.
Пример 3. Рассчитаем среднее линейное отклонение по данным о производительности труда работников одной смены по данным таблицы 29.

 

Таблица 29.