Статистика синергия. Статистика. Литература по теме Практические задания
 Скачать 1.83 Mb. Скачать 1.83 Mb.
|
|
Тема 8. Анализ взаимосвязи между социально-экономическими явлениями Цель изучения темы состоит в формировании системы знаний и компетенций об основных статистических категориях выявления и оценки силы взаимосвязи между социально-экономическими явлениями, способах расчета, оценки и интерпретации показателей взаимосвязи между социально-экономическими явлениями, выраженными неколичественными признаками. В результате успешного освоения темы Вы: Узнаете: · какие виды взаимосвязи существуют в экономическом анализе; · какие методы используются при изучении связей между социально-экономическими явлениями; · что представляют собой линейная и нелинейная связи; · что означает взаимная сопряженность признаков и каким образом подготовить исходные данные для ее оценки; · с помощью каких коэффициентов измеряется взаимосвязь между качественными признаками. Приобретете компетенции: · владение методами количественного анализа, теоретического и экспериментального исследования; · владение основными методами, способами и средствами получения, хранения, переработки информации, навыками работы с компьютером как средством управления информацией; · понимание роли и значения информации в развитии современного общества и экономических знаний; · способность оценивать воздействие макроэкономической среды на функционирование организаций и органов государственного и муниципального управления; · умение применять количественные и качественные методы анализа при принятии управленческих решений; · умение различать виды взаимосвязи; · умение строить и анализировать диаграмму рассеяния; · умение составлять таблицы взаимной сопряженности качественных признаков размерностью 2х2 и большей; · умение выбирать вид и рассчитывать значения коэффициентов взаимосвязи между качественными признаками. В процессе освоения темы акцентируйте внимание на следующих ключевых понятиях: · факторные и результативные признаки; · функциональная связь; · корреляционная связь; · прямая и обратная связь; · линейная и нелинейная связь; · ложная корреляция; · диаграмма рассеяния; · таблица сопряженности; · коэффициент ассоциации; · коэффициент контингенции; · коэффициент взаимной сопряженности Пирсона; · коэффициент взаимной сопряженности Чупрова; · показатель взаимной сопряженности. Вопросы темы: 1. Классификация видов и методов изучения взаимосвязи. 2. Графический метод выявления взаимосвязи. 3. Изучение взаимосвязи между качественными признаками. Теоретический материал по теме Вопрос 1. Классификация видов и методов изучения взаимосвязи. Исследование объективно существующих связей между социально-экономическими явлениями и процессами является важнейшей задачей статистики. Понимание, как изменение одного из исследуемых показателей отразится на изменении другого, необходимо при регулировании и управлении любыми системами и процессами, чтобы правильно оценивать последствия принимаемых управленческих решений. Большинство финансово-экономических процессов – это результат одновременного взаимодействия большого числа составляющих их элементов, представляющих собой выраженные в форме показателей различные количественные и качественные признаки. Признаки по их сущности и значению для изучения взаимосвязи делятся на два класса. Признаки, обуславливающие изменения других связанных с ними признаков, называются факторными, или просто факторами и обозначаются Х. Признаки, изменяющиеся под действием факторов, называются результативными и обозначаются Y. При исследовании взаимосвязи между одним факторным и одним результативным признаками или между двумя факторными признаками говорят о двумерных данных, а при изучении влияния нескольких факторных признаков на один результативный – о многомерных данных. В статистике различают функциональную и корреляционную связи. Функциональной называют связь, при которой определенному значению факторного признака соответствует одно и только одно значение результативного признака. Если зависимость проявляется не в каждом отдельном случае, а в общем, среднем, при большом числе наблюдений, то такая зависимость называется корреляционной. При корреляционной связи изменение среднего значения результативного признака обусловлено изменением признака-фактора и при одинаковом значении факторного признака величина признака-результата у разных единиц совокупности может в силу индивидуальных особенностей различаться. Связи между явлениями и их признаками классифицируются по направлению, тесноте (силе связи) и аналитическому выражению (рис. 20) 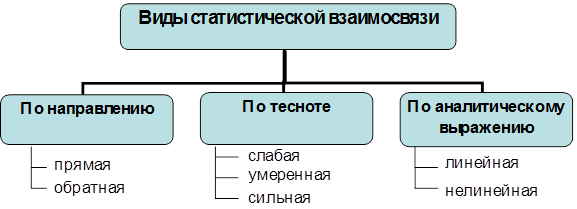 Рис. 20. Классификация видов взаимосвязи По направлению выделяют связь прямую и обратную. Прямая – это связь, при которой с увеличением или с уменьшением значений факторного признака происходит увеличение или уменьшение значений результативного признака. Так, рост объемов производства способствует увеличению прибыли предприятия. В случае обратной связи значения результативного признака изменяются под воздействием факторного, но в противоположном направлении – с увеличением или с уменьшением значений факторного признака происходит уменьшение или увеличение значений признака-результата. Так, снижение себестоимости единицы производимой продукции вызывает рост прибыли. Для измерения тесноты связи используют значение коэффициента корреляции. Он изменяется в пределах от -1 до +1. Знак (+) говорит о прямой связи, а (-) об обратной (табл. 41): Таблица 41. Количественные критерии оценки тесноты связи
По аналитическому выражению выделяют связи линейные и нелинейные. Если статистическая связь между явлениями X и Y может быть приблизительно выражена уравнением прямой линии ( Для выявления и анализа связи статистика использует следующие основные методы: · графический метод – построение диаграммы рассеяния; · метод корреляционного анализа – выявление наличия, силы и направления взаимосвязи между признаками; · метод регрессионного анализа – построение модели взаимосвязи, позволяющей получать расчетные значения результативного показателя на основе значений факторного признака. Причинную обусловленность и корреляцию нельзя считать синонимами. Корреляция не всегда дает объяснение, почему исследуемые переменные в двумерной совокупности связаны между собой. Следует иметь в виду, что корреляция бывает и без причинной обусловленности: она представляет собой число, которое говорит, что большим значениям одного фактора соответствуют большие значения другого (или наоборот). Корреляция всего лишь указывает, что между этими величинами наблюдается определенное соответствие. Наиболее распространенной причиной существования корреляции без причинной обусловленности является наличие некоторого скрытого третьего фактора, создающего впечатление, будто одна переменная выступает причиной другой. Однако реальной причиной для каждой из этих двух переменных является неизвестная третья. Под термином ложная корреляция понимают высокую корреляцию, которая обеспечивается действием третьего фактора. Например, если рассчитать значение коэффициента корреляции между такими показателями, как «размер ущерба имуществу от пожара» и «количество пожарных, участвовавших в тушении пожара», то это будет величина, близкая к 1. Однако, конечно же, нельзя утверждать, что причиной высокого размера ущерба является большое количество пожарных, действиями которых и нанесен ущерб имуществу. Безусловно, пожарные, заливая огонь пеной или водой, могут нечаянно повредить электрокабели или офисную технику, но в любом случае причиной высокой корреляции между ущербом имуществу и количеством пожарных является третий фактор – масштаб самого пожара. Чем более сложный и масштабный пожар, тем больший урон имуществу он наносит и тем большее число пожарных требуется для его тушения. Вопрос 2. Графический метод выявления взаимосвязи. Графический метод предполагает изображение взаимосвязи двух признаков с помощью диаграммы рассеяния (поля корреляции). Диаграмма рассеяния представляет каждую единицу совокупности в виде точки в пространстве двух измерений, соответствующих двум факторам. Переменная, которая рассматривается как «причина», обозначается х и указывается на оси абсцисс. Переменная, изменяющаяся под влиянием этой причины, обозначается y и указывается по оси ординат. Для построения диаграммы рассеяния необходимо в системе координат на оси Х отложить значения факторного признака, а на оси Y – результативного и каждое пересечение линий, проводимых через эти оси, обозначить соответствующими точками. Чем сильнее связь между признаками, тем теснее будут группи
роваться точки вокруг определенной линии, выражающей форму связи (рис. 21).  Рис. 21. Диаграмма рассеяния (поле корреляции) При отсутствии связи диаграмма рассеяния точек имеет вид либо круглого, либо овального облака (причем овал может быть направлен как горизонтально, так и вертикально, но не иметь наклона) (рис. 22). 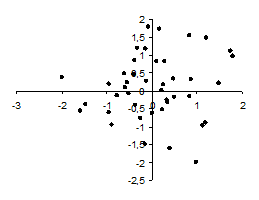 Рис. 22. Диаграмма рассеяния, свидетельствующая об отсутствии взаимосвязи между двумя признаками Легче всего поддается анализу и интерпретации двумерная совокупность данных, выраженная в форме линейной взаимосвязи. Визуально взаимосвязь проявляется в том, что точки на диаграмме рассеяния концентрируются вокруг условной прямой линии. Они могут как довольно тесно концентрироваться, почти точно попадая на прямую линию (рис. 23), так и быть разбросаны достаточно широко, образуя некоторое облако (рис. 24). Рис. 23. Диаграмма рассеяния, выражающая линейную положительную взаимосвязь 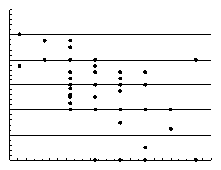 Рис. 24. Диаграмма рассеяния, выражающая линейную отрицательную взаимосвязь При нелинейной взаимосвязи точки на диаграмме рассеяния группируются вокруг некоторой кривой линии. Поскольку разновидностей кривых линий существует множество, анализ такой взаимосвязи существенно осложнен. Приведем пример двух наиболее распространенных видов нелинейной связи (рис. 25 и 26): Рис. 25. Диаграмма рассеяния, характеризующая взаимосвязь, выраженную уравнением гиперболы Рис. 26. Диаграмма рассеяния, характеризующая взаимосвязь, выраженную уравнением параболы Пример 1. Построим диаграмму рассеяния по данным таблицы 42 и охарактеризуем тип взаимосвязи, которую иллюстрирует диаграмма рассеяния. Таблица 42. Итоги работы менеджеров по продаже полиграфической продукции
При построении диаграммы рассеяния для данной двумерной совокупности данных необходимо, во-первых, определить факторный и результативный признаки. Так как затраченные усилия влияют на результат, следовательно, число контактов с клиентами признаем факторным признаком и изображаем его на горизонтальной оси, а объем продаж – результативным признаком и располагаем его по вертикальной оси. Далее изображаем точки, иллюстрирующие, как величина объема продаж изменяется от количества контактов. Нанеся все точки на график, получим диаграмму рассеяния, которая представлена на рис. 27. 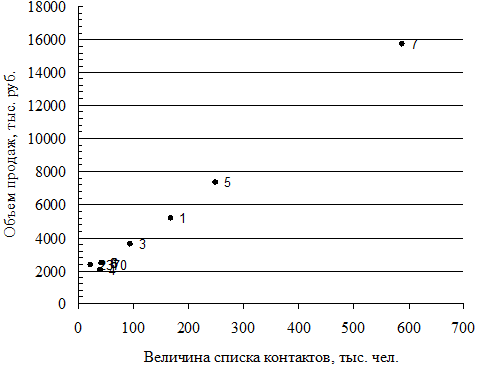 Рис. 27. Взаимосвязь между количеством контактов и объемом продаж полиграфической продукции На диаграмме рассеяния представлена информация как о каждой отдельной единице совокупности, так и о взаимосвязи между ними. Взаимосвязь между количеством контактов и объемом продаж можно признать положительной: точки на диаграмме выстраиваются снизу вверх при движении слева направо. Это свидетельствует о том, что менеджеры, имеющие больше количество контактов с клиентами, обеспечили компании и большие объемы сбыта (чем больше значения х, тем выше расположены точки на диаграмме). Полученную взаимосвязь можно признать линейной, что видно и по форме области концентрации точек на диаграмме рассеяния, которые практически выстраиваются в прямую линию. Вопрос 3. Изучение взаимосвязи между качественными признаками. Значения бизнес-показателей, анализируемых в ходе исследования, не всегда имеют количественное выражение. При обработке информации менеджер-аналитик часто сталкивается с показателями, выраженными в номинальной шкале, например: пол, должность сотрудника, уровень профессионального образования и т.п. Также информация может быть представлена по альтернативным признакам, принимающим только два варианта «да» (1) и «нет» (0) (например: курение сотрудника, наличие или отсутствие у него детей, наличие/отсутствие замечаний за нарушение производственной дисциплины и т.п.). При экспресс-опросах, например, по результатам обучающих мероприятий, используются вопросы, призванные выявить степень удовлетворенности участников обучения его результатами (удовлетворен / не удовлетворен), изменение отношения к предмету обучения (изменилось / не изменилось, ниже среднего / среднее / выше среднего, улучшилось / не изменилось / ухудшилось). Такие показатели являются качественными, и известные методы количественного анализа для их анализа и исследования неприменимы. Для определения тесноты связи двух качественных признаков, каждый из которых состоит только из двух вариантов, применяются коэффициенты ассоциации и контингенции. Для их вычисления строится таблица сопряженности [2 х 2], которая показывает связь между двумя явлениями, каждое из которых состоит из двух качественно отличных друг от друга значений признака (например, изделие годное или бракованное). Как правило, в строках располагают варианты факторного признака, а в столбцах – результативного. Если признак один и тот же, а различие состоит в объектах, то в строках и столбцах используют одинаковый порядок расположения вариантов. Например, исследуя взаимосвязь между факторным признаком «наличие высшего образования у родителей (имеют / не имеют)» и «наличие высшего образования у детей (имеют / не имеют)», вариант «имеет высшее образование» следует расположить в первой строке и в первом столбце таблицы сопряженности этих признаков. Таблица 43. Таблица взаимной сопряженности для вычисления коэффициентов ассоциации и контингенции
Коэффициент ассоциации Ка вычисляют по формуле: где n11 – число единиц, имеющих значения x1 и y1; n12 – число единиц, имеющих значения x1 и y2; n21 – число единиц, имеющих значения x2и y1; n22 – число единиц, имеющих значения x2и y2. Коэффициент ассоциации принимает значения в интервале [-1; 1]. При равенстве коэффициента ассоциации нулю говорят об отсутствии связи между изучаемыми признаками. Коэффициент контингенции Кк считается более надежной мерой связи и определяется по формуле: 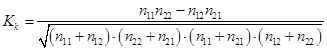 (68) (68)Коэффициент контингенции принимает значения в интервале [0; 1]. Коэффициент контингенции принимает нулевое значение при отсутствии связи между изучаемыми показателями и равен единице – при функциональной зависимости между ними. Коэффициент контингенции всегда меньше коэффициента ассоциации. Связь считается подтвержденной, если Пример 2. Исследуем связь между активностью участия студентов в практических занятиях и результатом тестирования по теме курса. Результаты обследования характеризуются следующими данными (таблица 44). Таблица 44. Зависимость результата тестирования по теме от активности участия студентов в практических занятиях
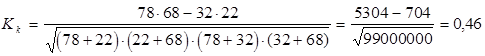 Таким образом, связь между результатом прохождения итогового тестирования по теме и активностью участия студента в практическом занятии сильная и прямая. Когда хотя бы один из качественных признаков принимает более двух вариантов значений, то для определения тесноты связи применяются коэффициенты взаимной сопряженности Пирсона и Чупрова. Вспомогательная таблица, используемая для расчета коэффициентов, имеет следующий вид: Таблица 45. Вспомогательная таблица для расчета коэффициентов взаимной сопряженности Пирсона и Чупрова
Коэффициент Пирсона КП и коэффициент Чупрова КЧ вычисляются по следующим формулам: 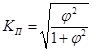 (69) (69)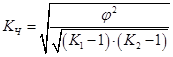 (70) (70)где K1 – число значений (групп) первого признака; K2 – число значений (групп) второго признака; – показатель взаимной сопряженности. Показатель взаимной сопряженности определяется как сумма отношений квадратов частот каждой клетки таблицы к произведению итоговых частот соответствующего столбца и строки. 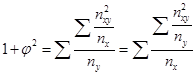 (71) (71)Вычитая из этой суммы «1», получим величину : 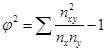 (72) (72)Коэффициенты взаимной сопряженности принимают значения в интервале [0; 1]. Равенство коэффициентов нулю означает отсутствие связи, равенство единице – полную взаимосвязь. Пример 3. С помощью коэффициентов взаимной сопряженности Пирсона и Чупрова исследуем взаимосвязь показателей «частота опозданий сотрудника» и «оценка качества работы сотрудника его руководителем». Таблица 46. Зависимость оценки качества работы сотрудника его руководителем от частоты опозданий сотрудника
Решение: 1. Рассчитаем показатель взаимной сопряженности : 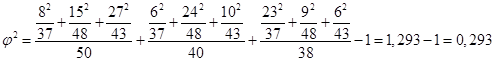 2. Найдем значения коэффициентов взаимной сопряженности согласно формулам: Таким образом, связь между частотой опозданий сотрудников и оценкой качества их работы руководителем можно признать статистически значимой и средней по силе влияния. Вопросы для самопроверки: 1. В чем различия между функциональной и корреляционной связью? 2. В каких случаях можно говорить о прямой, а в каких – об обратной зависимости между изучаемыми признаками? 3. Что такое диаграмма рассеяния и как она строится? 4. Как выглядит расположение точек на диаграмме рассеяния: а) при нелинейной связи между x и y; б) при отсутствии взаимосвязи между x и y? 5. Что такое ложная корреляция? 6. Что представляет собой таблица сопряженности? Какие размерности таблиц сопряженности вы знаете? 7. Для каких качественных данных используется расчет коэффициента ассоциации и контингенции? 8. Когда для оценки взаимосвязи используются коэффициенты взаимной сопряженности Пирсона и Чупрова? 9. Как интерпретируются количественные значения коэффициентов взаимной сопряженности? Какие критические значения для них существуют? 10. Какие коэффициенты следует применить для оценки взаимосвязи между показателями: а) «пол сотрудника» и «наличие ученой степени»? б) «уровень образования сотрудника (полное среднее, среднее профессиональное, высшее)» и «оценка степени корпоративной лояльности» (высокая, средняя, низкая)»? Литература по теме: Основная литература: 1. Улитина Е.В. Статистика: учеб. пособие / Е.В. Улитина, О.В. Леднева, О.Л. Жирнова. – 3-е изд. – М.: МФПУ, 2013.– 312 с. – (Университетская серия). Дополнительная литература: 1. Общая теория статистики: статистическая методология в изучении коммерческой деятельности: учебник / Под ред. А.А. Спирина, О.Э. Башиной. – М.: Финансы и статистика, 2004. 2. Практикум по теории статистики: учеб. пособие / Под ред. проф. Р.А. Шмойловой. – М.: Финансы и статистика, 2004. 3. Шмойлова Р.А., Минашкин В.Г., Садовникова Н.А., Шувалова Е.Б. Теория статистики: учебник / Под ред. проф. Р.А. Шмойловой. – М.: Финансы и статистика, 2004. 4. Методологические положения по статистике. – М.: Госкомстат России, 2010. Практические задания: Задание 1. При помощи диаграммы рассеяния оцените направление взаимосвязи между показателями, указанными в таблице.
Задание 2. По итогам проведения тренинга были получены следующие результаты анкетирования его участников (таблицы ниже). Посещаемость занятий сотрудниками
Таблица сопряженности оценки сотрудниками качества работы тренера и общей удовлетворенности посещением тренинга
При помощи известных вам методов определите: а) повлиял ли пол сотрудника на посещение занятий тренинга? б) есть ли взаимосвязь (и если есть, то какая) между оценкой участником тренинга работы тренера и общей оценкой его удовлетворенностью посещением тренинга? | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
