Лекции по цифровой электронике. Логические функции и логические элементы
 Скачать 2.34 Mb.
|
Законы алгебры логикиАЛ базируется на нескольких аксиомах, из которых выводят основные законы для преобразований с логическими переменными. Каждая аксиома представлена в двух видах, что вытекает из принципа дуальности логических операций, согласно которому операции конъюнкции и дизъюнкции допускают взаимную замену, если одновременно поменять 1 на 0, 0 на 1, знак на , а знак на . Аксиомы операции отрицания:  ,  .Аксиомы операций конъюнкции и дизъюнкции: 1а) 00=0 1б) 11=1 2а) 10=01=0 2б) 01=10=1 3а) 11=1 3б) 00=0 Законы АЛ вытекают из аксиом и также имеют две формы выражения а) и б).
а) ab=baб) ab=ba
а) a(bc)=(ab)c=abcб) a(bc)=(ab)c=abc
а) aa=a б) aa=a
а) a0=0 б) a0=a
а) a1=aб) a1=1
а) a  =0 б) a =1
а) a(bc)=ab+aб) a(bc)=(ab)( ac)
а) aab=a б) a(ab)=a
а) (ab)(a  )=aб) a.ba.=a
а)  б)  или после инвертирования в)  г)  Поскольку значениями логических функций могут быть только 0 или 1, то любые логические функции можно использовать как аргументы других логических функций, т.е. строить из простых функций более сложные. Пусть в таблице 1.2. задана произвольная функция Y трех аргументов, и ее нужно выразить с помощью простых функций НЕ, И, ИЛИ. Очевидно, что Y= 1, когда или a  c = 1 (строка 1), или  (строка 3), или  (строка 6), или  (строка 7). Таблица 1.2.
Все это можно записать в виде одного общего аналитического выражения:  (1.1)Полученное аналитическое выражение называют совершенной дизъюнктивной нормальной формой (СДНФ). СДНФ состоит из элементарных конъюнкций, соединенных знаками дизъюнкций. Конъюнкцию называют элементарной, если в нее не входит по несколько одинаковых букв. Число элементарных конъюнкций в СДНФ обязательно равно числу единичных значений функции в таблице истинности. В каждую элементарную конъюнкцию СДНФ входят обязательно все аргументы функции в прямой или инверсной форме. Поскольку процедуру построения СДНФ в принципе можно применить к таблице, содержащей любое число аргументов при любом расположении единичных значений функции, то можно сделать важный вывод: с помощью набора функций НЕ, И, ИЛИ можно выразить любую логическую функцию. Такой полный набор называют логическим базисом или просто базисом. Нетрудно показать, что базисами являются также и другие наборы: НЕ, И; НЕ, ИЛИ; И-НЕ и ИЛИ-НЕ. Д 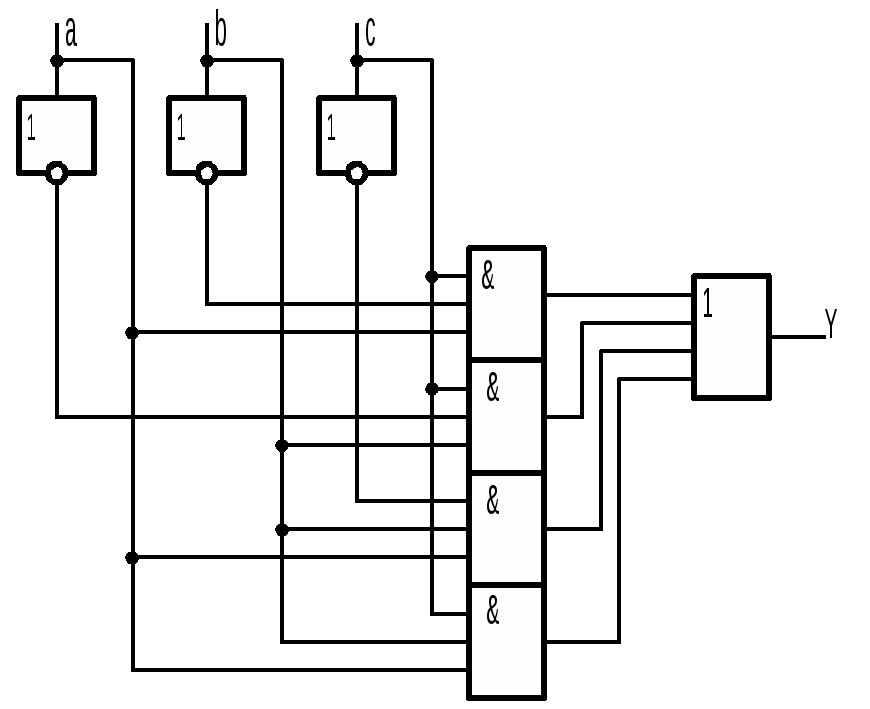 ля построения логической схемы, реализующей функцию, заданную таблицей истинности, обычно удобнее аналитическая форма представления функции. В данном случае - это выражение (1.1). Схема, реализующая (1.1), показана на рис. 1.6. Она состоит из трех ярусов. В первом ярусе расположены инверторы. Очевидно, что максимальное число инверторов не превышает числа аргументов. Во втором ярусе расположены элементы И, реализующие входящие в формулу элементарные конъюнкции. Число входов каждого элемента равно числу аргументов реализуемой функции, а число элементов- числу элементарных конъюнкций в формуле. В третьем ярусе схемы стоит элемент ИЛИ, число входов которого равно числу дизъюнкций в формуле.Рис.1.6. Логическая схема, реализующая (1.1). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
=a