Практическое задание 1. Занятие по теме Исследование основных логических элементов

• Название: Занятие по теме Исследование основных логических элементов
• Дата: 17.11.2020
• Размер: 243.51 Kb.
• Имя файла: Практическое задание 1.docx
• Тип: Занятие; #151215

Практическое занятие по теме «Исследование основных логических элементов»

Цель работы: Изучить основные логические элементы и базовые логические функции, научиться строить логические схемы по заданным логическим выражениям.

Теоретические сведения

1. 
   В алгебре логике используются следующие логические функции:
   

	Логическая функция	Операция	Связки и знаки для записи операции	Схематическое изображение логического элемента		Таблица истинности	Определение
				Отечественный вариант	Зарубежный вариант
1	Конъюнкция	Логическое умножение	И, AND, ^, ∙, &		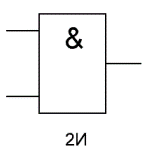	X1 X2 F 0 0 0 0 1 0 1 0 0 1 1 1	Конъюнкция-логическая операция, ставящая в соответствие двум простым высказываниям составное, являющееся истинным, когда оба исходных высказывания истинны
2	Дизъюнкция	Логическое сложение	ИЛИ, OR, V, |, +		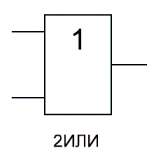	X1 X2 F 0 0 0 0 1 1 1 0 1 1 1 1	Дизъюнкция-логическая операция, ставящая в соответствие двум простым высказываниям составное, являющееся истинным, когда хотя бы одно или оба из исходных высказываний истинны
3	Инверсия	Логическое отрицание	НЕ, NOT, ¯, ¬		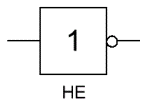	X1 F 0 1 1 0	Инверсия –логическая операция, которая исходному высказыванию ставит в соответствие новое высказывание, противоположное по значению исходному.
4	Конъюнкция с отрицанием	Логическое умножение с отрицанием	NAND		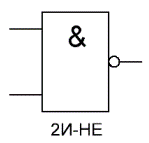	X1 X2 F 0 0 1 0 1 1 1 0 1 1 1 0	Конъюнкция с отрицанием – логическая операция, ставящая в соответствие двум простым высказываниям составное, являющееся истинным, когда хотя бы одно из исходных высказываний ложно
5	Дизъюнкция с отрицанием	Логическое сложение с отрицанием	NOR		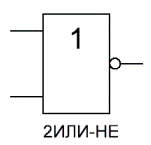	X1 X2 F 0 0 1 0 1 0 1 0 0 1 1 0	Дизъюнкция с отрицанием – логическая операция, ставящая в соответствие двум простым высказываниям составное, являющееся истинным, когда оба исходных высказывания – ложны.
6	«Исключающее ИЛИ» -	Сложение по модулю 2 (неравнозначность)	XOR		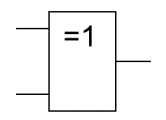	X1 X2 F 0 0 0 0 1 1 1 0 1 1 1 0	Исключающее ИЛИ – логическая операция, ставящая в соответствие двум простым высказываниям составное, являющееся истинным когда исходные высказывания противоположны друг другу по значению
7	Импликация	Логическое следование	Если…, то… =>		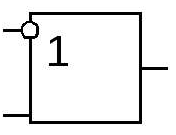	X1 X2 F 0 0 1 0 1 1 1 0 0 1 1 1	Импликация – логическая операция, ставящая в соответствие двум простым высказываниям составное, являющееся ложным когда условие (первое высказывание) истинно, а следствие (второе высказывание) ложно
8	Эквиваленция	Равнозначность	Тогда и только тогда , <=>		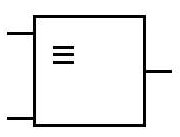	X1 X2 F 0 0 1 0 1 0 1 0 0 1 1 1	Эквиваленция – логическая операция, ставящая в соответствие двум простым высказываниям составное высказывание, являющееся истинным, когда оба исходных высказывания одновременно ложны или одновременно истинны

2. 
   Приоритет логических операций
   

• 
  Инверсия
  
• 
  Конъюнкция
  
• 
  Дизъюнкция
  
• 
  Импликация
  
• 
  Эквиваленция
  

3. 
   Алгоритм построения таблицы  истинности:
   

1. подсчитать количество переменных n в логическом выражении;

2. определить число строк в таблице по формуле m=2n, где n - количество переменных;

3. подсчитать количество логических операций в формуле;

4. установить последовательность выполнения логических операций с учетом скобок и приоритетов;

5. определить количество столбцов: число переменных + число операций;

6. выписать наборы входных переменных;

7. провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной в пункте 4 последовательностью.

Заполнение таблицы:

1. разделить колонку значений первой переменной пополам и заполнить верхнюю часть «0», а нижнюю «1»;

2. разделить колонку значений второй переменной на четыре части и заполнить каждую четверть чередующимися группами «0» и «1», начиная с группы «0»;

3. продолжать деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами «0» или «1» до тех пор, пока группы «0» и «1» не будут состоять из одного символа.

4. 
   Алгоритмпостроение логических схем.
   

1. 
   Определить число логических переменных;
   
2. 
   Определить количество базовых логических операций и их порядок;
   
3. 
   Изобразить для каждой логической операции соответствующий ей логический элемент (вентиль);
   
4. 
   Соединить логические элементы (вентили) в порядке выполнения логических операций.
   

5. 
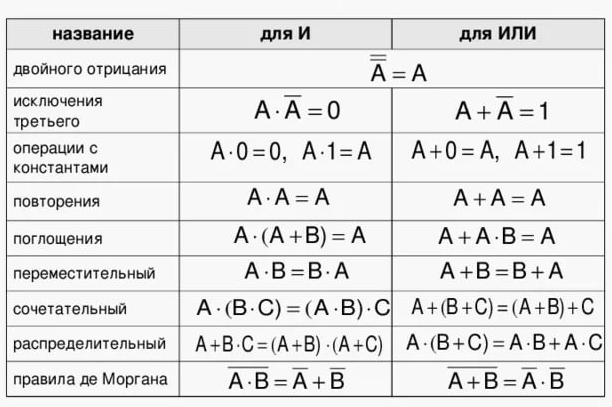
   Законы алгебры логики
   

Практическая часть
Задание 1.

• 
  Открыть программу для моделирования работы логических схем по ссылке https://logic.ly/demo
  
• 
  Запустить Adobe Flash Player. В появившемся окне щелкнуть по кнопке Разрешить
  
• 
  С помощью данной программы доказать истинность основных законов алгебры логики, путем построения логической схемы по логической формуле
  

Задание 2.

• 
  Создать в программе модели логических схем согласно вариантам, указанным преподавателем из таблицы 1
  
• 
  Исследовать работу данных моделей.
  
• 
  Оформить результаты исследований (п.4) в письменном отчете, который должен содержать:
  

• 
  логическое выражение;
  
• 
  рисунок логической схемы по ГОСТ (отечественному стандарту);
  
• 
  таблицу истинности.
  

Задание 3.

Построить таблицы истинности для следующих выражений : A v (B v ¬B => ¬ C); A & (B & ¬ B => ¬ C); A v (B v ¬B) & A v (B => C)
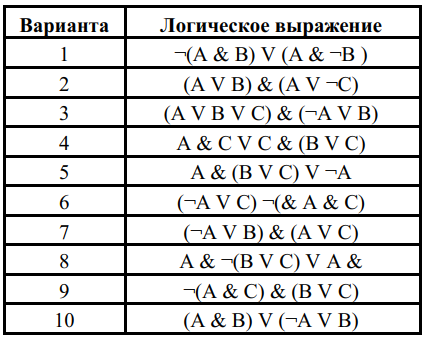Т аблица 1