Логика КР. Шпоры логика. Логика это наука о формах и законах правильного мышления. Предмет логики
 Скачать 467.25 Kb. Скачать 467.25 Kb.
|
|
П р о т и в о п о с т а в л е н и е – логическая операция с простыми суждениями, производящая одновременно и обращение, и превращение суждений. Делать это можно в разной последовательности. Либо вначале исходное суждение обращается («Все S есть Р» → «Некоторые Р есть S»), а затем обращенное суждение превращается («Некоторые Р есть S» → «Некоторые Р не-есть не-S»). Либо вначале исходное суждение превращается («Все S есть Р» → «Все S не-есть не-Р»), а затем превращенное суждение обращается («Все S не-есть не-Р» → «Все не-Р не-есть S»). Противопоставление субъекту. Противопоставление субъекту - это такая логическая операция с простым суждением, в результате которой образуется новое суждение, субъектом которого является предикат исходного суждения, а предикатом - понятие, противоречащее субъекту исходного суждения. Общая последовательность данной операции такова: Исходное суждение Обращение исходного суждения Превращение обращенного суждения. Противопоставление предикату. Противопоставление предикату - это такая логическая oперация с простым суждением, в результате которой образуется новое суждение, субъектом которого является понятие, противоречащее предикату исходного суждения, а предикатом - субъект исходного суждения. Общая последовательность данной операции такова: Исходное суждение Превращение исходного суждения Обращение превращенного суждения. 13. Сложные суждения. Логический союз. С л о ж н о е суждение – это суждение, которое состоит из двух и более простых суждений, связанных между собой логическими союзами. Из определения ясно, что сложные суждения образуются из простых суждений и логических союзов. Таблица основных логических связок.
14. Логическое значение сложных суждений: таблицы истинности. Условия истинности сложных суждений, состоящих из простых категорических суждений, основываются на допущении двузначности и задаются при помощи таблиц истинности. Таблица истинности для конъюнкции
Таблица истинности для дизъюнкции
С л а б а я дизъюнкция истинна, когда истинен хотя бы один из членов дизъюнкции, и ложна, когда все ее члены – ложны
С и л ь н а я дизъюнкция истинна только при разных логических значениях членов дизъюнкции и ложна при одинаковых. Таблица истинности для импликации
Таблица истинности для эквиваленции
Таблица истинности для отрицания
«Отрицание» – унарный союз. Если исходное суждение истинно, то его отрицание – ложно, и наоборот. 15. Умозаключение как форма мышления. Структура и виды умозаключений. Умозаключение - форма мышления, посредством которой из одного и более суждений выводится новое суждение. Новое суждение может быть и ложным. Зависит от: Являются ли истинными исходные суждения, правильно ли они связаны между собой. Истинность мысли и правильность мысли: Первое условие связано с истинностью мысли, второе - правильность мышления. Истинное мышление - мышление, адекватно отражающее фрагмент действительности Правильное мышление - мышление, не нарушающее правил и законов логики. Ложность посылок - когда исходные суждения ложны, то правила вывода не нарушены. Неправильность вывода - когда исходные суждения истинны, но нарушается определённое логическое правило. Структура умозаключения - посылки, заключения (вывод). Посылки - исходные суждения, вывод - новое суждение. Виды умозаключений :1. По числу посылок (непосредственные и посредственные) Непосредственные - одна посылка и одно умозаключение. Умозаключения - обращения, превращения, противопоставления, все заключения по логическому квадрату.Например в непосредственным относятся: - умозаключение обращения E суждения, - обращение A суждения, обращение I.... - превращения... - противопоставления субъекту/предикату Опосредованные умозаключения состоят из двух и более посылок и заключений. S-P S-P ---- S-P 2. По направленности логического вывода (дедуктивные, индуктивные, традуктивные) Дедуктивные - рассуждение от общего к частному Индуктивные - от частного к общему Традуктивные - объём знаний в посылках и заключениях одинаков. 16. Простой категорический силлогизм: правила, фигуры, модусы. Простой категорический силлогизм - дедуктивное опосредованное умозаключение, состоящее из двух суждений, имеющих субъектно-предикатную форму. Или - дедуктивное опосредованное умозаключение, состоящее из двух простых категорических суждений и заключения. Структура ПКС : Силлогизм (ПКС) - Состоит из трёх категорических суждения, 2 из них образуют посылки, 3 - заключение. Силлогизм - состоит из трёх терминов. Больший термин (совпадает с предикатом) - P. Меньший (совпадает с субъектом) - S. Средний (присутствует в каждой посылке, но нету в заключении) - M. M-P Все государства имеют столицу S-M Конго - государство ---- S-P - Конго имеет столицу ПКС - это умозаключение об отношении двух крайних терминов на основании их отношения к среднему термину. Правило термина силлогизма - в силлогизме должно быть три и только три термина, 2 - мало, 4 - много. Для записи ПКС можно использовать разные формы. В ПКС средний термин может занимать место S или P. Поэтому различают 4 вида силлогизма: 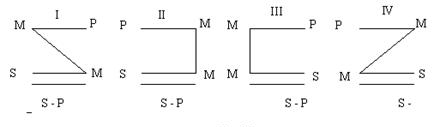 Различное положение среднего термина в разных фигурах хорошо видно при их сравнительном графическом изображении. 1) M замещает S в большей посылке и P в меньшей 2) M замещает P в обеих посылках 3) M замещает S в обеих посылках 4) M замещает P в большей посылке и S в меньшей Фигуры силлогизма - это разновидности силлогизма, различающиеся положением среднего термина в посылках. Правило фигур: 1 фигура. Большая посылка - суждение общее (A или E). Меньшая посылка - суждение утвердительное (А или I). 2 фигура. Большая посылка - суждение общее (A или E). Одна из посылок - суждение отрицательное (Е или O). 3 фигура. Меньшая посылка - суждение утвердительное (A или I). Заключение - суждение частное (I или O). 4 фигура. Если большая посылка - суждение утвердительное (А или I), то меньшая посылка - суждение общее (А или Е). Если одна из посылок - суждение отрицательное (Е или О), то большая посылка - суждение общее (А или Е). Если меньшая посылка - суждение утвердительное (А или I), то заключение силлогизма - суждение частное (О или I). Разновидности силлогизма, различающиеся количественными и качественными характеристиками посылок, называются модусами простого категорического силлогизма. Каждой фигуре отвечают модусы.  Отбор правильных модусов производится как с помощью общих правил силлогизма, так и дополнительных правил фигур силлогизма. В каждом латинском названии модуса есть 3 гласные. Первые 2 - это посылки, 3 - заключение. 17. Разновидности категорического силлогизма. разновидностей простого категорического силлогизма, образованного из простых суждений, также относятсясокращенный силлогизм (энтимема), сложныц (полисиллогизм) и сложносокращенный (эпихейрема). Энтимема. Силлогизм может быть полным (с выраженной полной структурой) и неполным (когда один из 3 элементов структуры не выражен явно, а лишь подразумевается). а) с пропущенной большей посылкой. б) с пропущенной меньшей посылкой. в) с пропущенным заключением. Если представить себе несколько связанных по смыслу простых силлогизмов, в которых заключение предшествующего силлогизма (его называют в логике просиллогизмом) становится посылкой последующего (эписиллогизма), то такая форма мысли называется полисиллогизмом. а) если заключение просиллогизма берется в качестве большей посылки эписиллогизма, то такой полисиллогизм называется прогрессивным. Он имеет вид. б) если заключение просиллогизма берется в качестве меньшей посылки эписиллогизма, то такой полисиллогизм называется р е г р е с с и в н ы м. Сорит (от греч. soros – куча) или сокращенный полисиллогизм. В такой форме вывода пропущены заключения простых силлогизмов, которые образуют бόльшую или меньшую посылки эписиллогизмов. Аналогично полисиллогизму, сориты бывают прогрессивными (гоклениевскими1) и регрессивными (аристотелевскими). В прогрессивном сорите пропущены бόльшие посылки эписиллогизмов В аристотелевском сорите пропущены меньшие посылки эписиллогизмов Э п и х е й р е м а (от греч. epiheirema – умозаключение) или сложносокращенный силлогизм, в котором обе посылки – энтимемы (в которых также могут быть пропущены как посылки, так и заключение). 18. Выводы из сложных суждений: условные и условно-категорические умозаключения. У с л о в н ы м называется силлогизм, в составе которого есть условное суждение. Условное суждение имеет структуру: «Если А, то В» или «p → q» В зависимости от того, состоит ли силлогизм только из условных суждений или нет, различают: ч и с т о у с л о в н ы й силлогизм. у с л о в н о – к а т е г о р и ч е с к и й силлогизм — это силлогизм, одна из посылок которого — условное суждение, а другая — категорическое. В символической логике они принимают следующий вид: 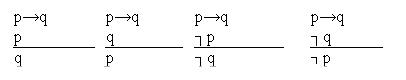 Достоверные модусы. М о д у с п о н е н с - утверждающий модус. «Утверждающим» он называется потому, что его заключение — утвердительное суждение М о д у с т о л л е н с - отрицающий модус. В данном случае рассуждение идёт не от утверждения основания к утверждению следствия (как в предыдущем модусе), а иначе: от отрицания следствия к отрицанию основания. Правдоподобные модусы. «От отрицания основания к отрицанию следствия» «От утверждения следствия к утверждению основания»: 19. Выводы из сложных суждений: разделительно-категорические умозаключения. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||