Логика КР. Шпоры логика. Логика это наука о формах и законах правильного мышления. Предмет логики
 Скачать 467.25 Kb. Скачать 467.25 Kb.
|
|
1. Предмет логики как науки. Основные формы мышления. Логика - это наука о формах и законах правильного мышления. Предмет логики - законы и формы, приемы и операции мышления, с помощью которых человек познает окружающий мир. Предмет логики - слово, понятие, разум, рассуждение. Изучение интеллектуальной деятельности человека! Одна из главных задач логики — определить, как прийти к выводу из предпосылок (правильное рассуждение) и получить истинное знание о предмете размышления, чтобы глубже разобраться в нюансах изучаемого предмета мысли и его соотношениях с другими аспектами рассматриваемого явления. Задача логики заключается в том, чтобы показать, каким правилам должно следовать умозаключение, чтобы быть верным. Мышление представляет собой разнообразные сочетания мыслей. Понятие = признак + признак... Суждение = понятие + понятие… Умозаключение = суждение + суждение... Понятие - отражает общие существенные признаки предметов. При помощи понятий мышление кодирует предметы реального мира и создает его идеальную модель. В уме мы говорим о мире на языке понятий. Суждение позволяет высказываться о наличии или отсутствии этих признаков у предметов (Мухомор не является съедобным). Это более сложная форма мысли, она состоит уже не из признаков, а из понятий и может быть истинной либо ложной. Умозаключение - самая сложная форма человеческой мысли, образованная из суждений. Благодаря умозаключению мы получаем знание о новых признаках на основании тех, которые уже известны (Все цитрусовые - теплолюбивы, а мандарин - цитрусовый. Значит, мандарин - теплолюбивое растение). 2. Фундаментальные законы логики. Аристотель сформулировал основные законы правильного мышления: закон тождества, закон непротиворечия, закон исключенного третьего. Позднее был сформулирован четвертый закон - закон достаточного основания. Данные законы имеют силу для всех форм мысли и выступают условиями правильности мышления. Закон мышления - необходимое, существенное, повторяющаяся связь между мыслями. Закон тождества - всякое понятие и суждение в процессе определения, рассуждения, доказательства должны быть тождественны сами себе. Он часто нарушается, когда идет подмена понятий (на турнире шахматист из-за растеренности потерял очки). Тождества - сходство предметов в каких-то отношениях (все жидкости упруги и теплопроводны). Закон противоречия или непротиворечия - два противоположных суждения об одном и том же предмете, взятом в одно и тоже время и в одном и том же отношении не могут быть одновременно истинны (все грибы являются съедобными; ни один гриб не является съедобным). Противоположные суждения делятся на: противные и противоречащие. Логический квадрат: А - общеутвердительные суждения I - часноутвердительные суждения Е - общеотрицательные суждения U - часноотрицательные суждения Закон исключенного третьего - два противоречащих суждения об одном и том же предмете, взятом в одно и тоже время и в одном и том же отношении не могут быть вместе истинными или ложными, одно из них истинно, другое ложно, третьего не дано. Противоречия не будет если: а) ручь идет о разных предметах (Осенью дождь полезен для грибов. Осенью дождь не полезен для уборки урожая). б) речь идет в разное время (этот букет роз свежий. Этот букет роз не свежий (через 2 недели)). Закон достаточного основания - всякая мысль в процессе определенного рассуждения, доказательства должна быть достаточно обоснованная (персики в карманах). 3. История логики. Логика классическая и неклассическая. Заслуга выявления форм мышления, а также основных законов, связывающих эти формы, принадлежит Аристотелю. Логику Аристотеля считают дедуктивной, поскольку в ней выведение нового знания есть переход от общего положения к частному случаю. Главный труд Аристотеля - "Органон" являлся каноном дедуктивного способа рассуждения. Он соответствовал типу преобладавших в античности наук и выступал их логико-методологическим основанием. В современной логике рассматриваются и другие формы мысли: вопрос, проблема, гипотеза.. Классическая логика - термин, используемый в математической логике по отношению к той или иной логической системе, для указания того, что для данной логики справедливы все законы (классического) исчисления высказываний, в том числе закон исключения третьего. Традиционно ориентиром классической логики служит анализ математических рассуждений, поэтому ее особенности связаны именно им. В процессе развития классическая логика оказалась одной из семейства логических теорий. Ядром современной логики традиционно остается классическая логика, сохраняющая как теоретическую, так, и практическую значимость. Неклассическая логика - логика, в которой один или несколько законов классической логики не выполняются. Самым известным примером неклассической логики есть интуиционистская логика (отказ от закона исключения третьего). Кроме того существуют некоммутативная логика (отказ от коммутативности конъюнкции и дизъюнкции), линейная логика (отказ от идемпотентности конъюнкции и дизъюнкции), немонотонная логика (отказ от монотонности отношения выводимости), квантовая логика (отказ от дистрибутивности ), и огромное множество других. 4. Понятие как форма мышления. Структура понятия. Простейшей формой мысли является понятие. Понятие = признак + признак. Понятие является мысленным отображением в сознании человека общих существенных признаков предметов. Предпосылкой образования понятия выступает способность нашего мышления сравнивать предметы между собой по различным признакам. Признаками называют сходства или различия предмета. Понятие - это мысль об общих существенных признаков предмета. Всё о чём можно думать, может быть предметом мысли. Поэтому понятие может содержать в себе признаки как материальных, реально существующих предметов, так и идеальных (пример, самого мышления),также вымышленных(вечный двигатель). Понятия возникают только в том случае, когда в них появляется потребность. Выражением наших мыслей является естественный язык. Язык делает мысль действительной. Смысловая единица - понятие, лексическая единица - слово. Понятие - это смысл слова. Понятие - это мысль о существенных признаках предметов, выраженная в слове или словосочетании. Структура понятия: Структура понятия определяется его ролью в мышлении и состоит из двух элементов: содержания и объёма. Содержание - важнейший элемент в структуре понятия. Это его качественный параметр. Содержание понятия есть совокупность существенных признаков, мыслимых в данном понятии, как отличительных, так и общих. Объём - в структуре понятия обозначает совокупность предметов мысли, обладающих одним содержанием, т.е. одними и теми же отличительными признаками. Объём выступает количественным параметром понятия. С увеличением содержания понятия его объём уменьшается, а с уменьшением содержания - объём увеличивается. 5. Виды понятий. П о с о д е р ж а н и ю понятия принято делить на: К о н к р е т н ы е и а б с т р а к т н ы е (конкретные понятия - это понятия о предметах («механическое устройство», «автобус», «растение», «диплом»). Абстрактные - это понятия о свойствах и отношениях («красивый», «безбилетный», «родной»). А б с о л ю т н ы е и о т н о с и т е л ь н ы е (абсолютные понятия безотносительны, самостоятельны, беспредпосылочны, в их содержании нет признаков, указывающих на их зависимость от других понятий, например «зрение», «наука», «инженер», в содержании относительных понятий имеются признаки, указывающие на те понятия, с которыми оно соотнесены по смыслу, и без которых они бессмысленны; относительными являются понятия «муж», «родители», «учитель», «жених». Трудно себе представить «мужа» без жены, «родителей» без детей, «учителя» без учеников, «жениха» без невесты), также относительными являются и «парные понятия» диалектической логики: «форма и содержание», «сущность и явление», «причина и следствие» и др., т.е. логика понятий отражает логику вещей); П о л о ж и т е л ь н ы е и о т р и ц а т е л ь н ы е (в положительных понятиях мыслится присутствие определенных признаков - «экономика», «техника», «спорт», в отрицательных понятиях фиксируется отсутствующий признак. Например, «нездоровый», «алогичный», «аморфный», «неподготовленный», отсутствие признака - это тоже признак). П о о б ъ е м у понятия делятся на следующие: н у л е в ы е: объем = 0 («король Беларуси», «Циклоп»); е д и н и ч н ы е: объем = 1 («основатель кибернетики», «создатель дизеля»); 3) о б щ и е: объем > 1 («станция», «космонавт»). Кроме того, п о х а р а к т е р у э л е м е н т о в, образующих объем, можно различать собирательные и несобирательные понятия. Они различаются типом отношений между отдельными элементами класса и всем классом элементов. Главная особенность собирательных понятий заключается в том, что в их содержании есть признаки, отсутствующие у отдельных элементов класса. К примеру, собирательными являются понятия: «Солнечная система», «Большая медведица», «коллегия адвокатов», «футбольная ассоциация», «дивизия». Напротив, признаки, содержащиеся в несобирательных понятиях, относятся как к классу предметов, так и к его отдельным элементам. Например, понятие «цветок» характеризует и весь класс цветов, и каждый цветок в отдельности - розу, ромашку, пион. 6. Отношения между понятиями. П о с о д е р ж а н и ю отношения между понятиями бывают сравнимыми и несравнимыми. С р а в н и м ы е - это понятия, в содержании которых имеются общие существенные признаки. Например, можно сравнивать понятия «спортсмен» и «студент», «учебный предмет» и «логика», «чувство» и «любовь». Н е с р а в н и м ы м и называются понятия, в содержании которых отсутствуют какие-либо общие признаки. Например, нельзя сравнивать понятия «закон Божий» и «ЭВМ», «монах» и «станция». В зависимости от того, как соотносятся признаки сравнимых понятий, последние делятся, в свою очередь, на следующие: Т о ж д е с т в е н н ы е, и л и р а в н о з н а ч н ы е понятия (признаки таких понятий полностью совпадают. В языке такие понятия выражаются синонимами, например, понятия «первый президент Республики Беларусь» и «А.Г.Лукашенко» тождественны); С х о д н ы е, и л и о д н о р о д н ы е понятия (у таких понятий общей является часть содержания, например, в содержании понятий «девушка» и «минчанка» есть общие признаки, образующие новое сложное понятие «девушка-минчанка»; «лес» и «парк» - «лесопарк». П о д ч и н е н н ы е понятия (данное отношение возникает тогда, когда признаки одного понятия полностью находятся в содержании другого понятия. Например, в отношении подчинения находятся понятия «периодическое издание» и «журнал»,«факультет БГУИР» и «ФИТУ», «язык программирования» и «Ассемблер», «офицер» и «подполковник». («подполковник» - это офицер, однако офицер не обязательно подполковник)). По объему: Понятия - несравнимые и сравнимые. Сравнимые - Совместимые и несовместимые. Совместимые - тождественные, однородные (а и б имеют одинаковые признаки), включение (б полностью включается в А) Несовместимые - противоположные (А - не А), противоречивые (А .. с .. не А), совместное включение (а и б включается в С). 7. Логические операции с понятиями: определение. Определение - раскрытие содержания понятия или термина. Определение - явное и неявное. Явное (Установка его характерных признаков.): функции (образовательная, эвристическая), виды (родовидовое, генетическое). Правила и ошибки явного определения понятий (4): Соразмерность -> расширенное, зауженное; Круг -> Тавтология; Определение через слова, которые тоже нужно пояснять -> неизвестное через неизвестное; отрицательное определение -> это - не то. Правильное определение должно быть достаточным, не содержать в себе простого повтора слов, других неясных слов, и, по возможности, положительным. Неявное определение (чаще встречается в науке): виды (описание, сравнение, характеристика (указание на личные свойства и признаки)). Остенсивные (показательные) и вербальные (словесные определения, без образных пояснений). 8. Логические операции с понятиями: деление, обобщение и ограничение. Деление понятия - раскрытие его объёма. Делимое - исходное понятие, которое требует установки объёма. Основание деления - признак, по которому производится деление. Члены (результаты) деления - это виды делимого понятия. Правила и ошибки деления: - Соразмерность (Делимое = сумма членов деления)->неполное, избыточное; - Деление по одному основания -> подмена признака (или основания) - Деление должно быть непрерывным и последовательным -> скачка в делении - Результаты деления должны исключать друг друга -> нечёткое деление (пример - продукты качественные и отечественные) Виды деления: - По видоизменения признака (по изменению признака) - Дихотомическое деление (рассечение понятия на 2 части: А - не А; наука: техническая, не техническая: ... ) Обобщение и ограничение - взаимообратная операция, демонстрирующая гибкую связь между содержанием и объёмом понятия и придающая мысли динамику. Обобщение - собака->животное (от понятия с меньшим объёмом к большему, путём уменьшения содержания) Ограничение - животное->собака (от понятия с большим объёмом к меньшему, путём увеличения содержания) 9. Суждение как форма мышления. Виды суждений. Суждение - понятие + понятие Суждение - это высказывание, утверждающее или отрицающее что-нибудь о чём-нибудь (Аристотель) Суждение - это связь понятий, это язык мыслей, понятие - это алфавит. Суждение может быть истинным или ложным Суждение состоит из субъекта (S), предиката (P) и связки (СТРУКТУРА) S - субъект. Предмет мысли. Подлежащее. P - предикат. Понятие, указывающее на свойство предмета. Логическая связка - логические отношения между S и P S есть/не есть P Виды суждения: Форма суждения зависит от способа его построения. Суждения делятся на качественные и количественные. Качественные - Категорические (S есть P), суждения отношений (равенство, подобие, одновременность, последовательность), модальные суждения (достоверность высказывания с точки зрения его необходимости, возможности, доказуемости). Качественные признак зависит от связки. Количественная характеристика зависит от квантора (все, не все, некоторые). Делятся на единичные, частные, общие. три основных вида суждения: К а т е г о р и ч е с к и е суждения или суждения принадлежности Суждения о т н о ш е н и й. М о д а л ь н ы е суждения. К а т е г о р и ч е с к и е суждения имеют структуру «S есть P». Суждения о т н о ш е н и й выражают не принадлежность, а различные типы отношений между предметами и свойствами: равенства(«Оценка равна знаниям»), подобия(«12:4 подобно 9:3»). М о д а л ь н ы е суждения (от лат modus- мера, способ) оценивают достоверность высказывания с точки зрения его «необходимости», «возможности» с точки зрения качества утвердительными («Все студенты пишут дипломные работы») и отрицательными («Х не сдал экзамен по математике»). По количеству суждения делятся на единичные, частные и общие. Е д и н и ч н о е суждение устанавливает принадлежность признака2 единственному предмету мысли. Ч а с т н о е суждение указывает на принадлежность признака нескольким предметам или части класса предметов. О б щ е е суждение констатирует принадлежность признака всем элементам класса, то есть исчерпывает весь объём класса. 10. Атрибутивные суждения: структура, виды, распределённость терминов. По количеству атрибутивные суждения бывают общими, частными и единичными. В общих суждениях предмет мысли (субъект) взят в полном объеме. В частных суждениях предмет мысли (субъект) берется в части объема. Единичные суждения информируют о конкретном единичном предмете Атрибутивное суждение состоит из трех элементов: 1) субъекта, 2) предиката и 3) связки. Субъект — выделяет предмет мысли (то, о чем говорится в суждении) и выполняет функцию логического подлежащего. Предикат — выражает мысль о предмете (то, что говорится в суждении) и выполняет функцию логического сказуемого. Связка — отношение между предметом мысли и его свойствами. У атрибутивных суждений есть две важнейшие характеристики: 1) количество и 2) качество. Количество — логическая характеристика суждения, раскрывающая, в каком объеме взят субъект суждения (полностью или частично). Качество — логическая характеристика суждения, выражающая наличие утверждения или отрицания в связке. 11. Отношения между атрибутивными суждениями: логический квадрат. Совместимость суждения может быть: полной, частичной(пересечение), подчинённой (включение). В логике есть 4 вида логический отношений между сравнимыми категорическими суждениями: - подчинение - противоречие (контрадикторности) - противоположности (контрарности) - подпротивоположности (субконтрарности) Логический квадрат: 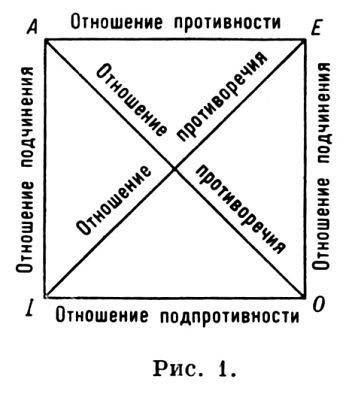   12. Операции с простыми суждениями. О б р а щ е н и е – одна из них. Логический смысл данной операции заключается в том, что субъект (S) и предикат (Р) суждения меняются местами, не меняя качества суждения. Количество может как сохраняться (при чистомобращении), так и меняться (обращение с ограничением). Общая структура этой операции такова:
Читается: «если S есть (не-есть) Р, то Р есть (не-есть) S». С учетом распределенности терминов, суждения типа А, Е, I, О обращаются следующим образом: А → I.
Суждение А обращается в суждение I: «Если все S есть Р, то некоторые Р есть S». Это обращение с ограничением. Ограничение связано с тем, что понятия S и Р взяты в разном объеме. A → A
Суждение А может также обращаться и в суждение A: «Если все S есть Р, то все Р есть S». Это обращение общеутвердительного суждения в общеутвердительное – обращение без ограничения Е → Е.
Суждение Е обращается в суждение Е без ограничения: «Если ни одно S не-есть Р, то ни одно Р не есть S». I → I.
Суждение I обращается в I также без ограничения, т.е. с сохранением качества и количества суждения: «если некоторые S есть Р, то некоторые Р есть S». П р е в р а щ е н и е – логическая операция с простыми суждениями, в ходе которой меняется качество суждения (утвердительная связка заменяется на отрицательную и наоборот), субъект и предикат остаются на своих местах (не обращаются), а предикат исходного суждения заменяется на противоречивый в превращенном суждении. Общая структура операции превращения:
Читается: «Если S есть (не-есть) Р, то S не-есть (есть) не-P». Операцию превращения можно производить со всеми видами простых суждений. При этом: А превращается в Е Е превращается в А I превращается в О О превращается в I А → Е. Общеутвердительные суждения превращаются по формуле:
Е → А. Общеотрицательные суждения превращаются по формуле:
I → O. Частноутвердительные суждения превращаются по формуле:
O → I. Частноотрицательные суждения превращаются по формуле:
|
