Логика_формальные языки. Логика формальные языки как системы и средства моделирования. Основные определения. Формальные языки
 Скачать 154.05 Kb. Скачать 154.05 Kb.
|
|
Логика_формальные языки как системы и средства моделирования. Основные определения. 1. ФОРМАЛЬНЫЕ ЯЗЫКИ Предметом математической логики являются, прежде всего, математические теории. При этом слово "теория" понимается в некотором специальном смысле. Под теорией в математической логике понимают формализованный язык L вместе с некоторым множеством предложений (формул) языка. Чтобы грамматический анализ языка был однозначен, правила его образования должны носить четкий характер. Элементами языка являются символы (буквы) и различные наборы символов, которые называют выражениями. Правильно составленные выражения, которым в данном языке придается определенный смысл, называют отмеченными выражениями. Символы языка - буквы образуют множество минимальных выражений (под минимальными понимаются выражения, не разложимые на составляющие) - алфавит в широком смысле, так как в него включены скобки, знаки препинания, пробелы и т.д. Пусть некоторое множество S является множеством символов языка L. Каждое выражение языка есть конечная последовательность символов, e = (s1, s2, ..., sn). Выражение e можно представить как функцию, определенную на множестве {1, 2, ..., n} со значениями в S, e(1)=s1, e(2)=s2, ..., e(n)=sn. Выполняется свойство единственности разложения выражения, т.е. если e=s1,s2,...,sn и e=t1,t2,...,tm, то n=m и s1=t1,...,sn=tn. Грамматичестий анализ основан на распознавании сложного выражения как результата сопряжения более простых выражений. На множестве всех выражений Е введем бинарную операцию (умножение), определив произведение выражений e=s1,s2,...,sn и f=t1,t2,...,tm как ef=(s1,s2,...,sn,t1,t2,...tm). Введенная операция подчиняется ассоциативному закону (ef)g=e(fg). Кроме того, если ввести выражение нулевой длины e0, то e0 e = e e0 =e; e0 играет роль единицы и множество выражений языка - Е с введенной операцией образует полугруппу с единицей. 1.1. Классификация отмеченных выражений. Классификация выражений абстрактного языка начинается с символов языка. В общем случае абстрактный язык включает девять категорий символов - четыре счетных класса: класс переменных; класс констант; класс функциональных символов; класс символов отношений; и пять категорий, включающих по одному символу - логические связки: символ отрицания; символ дизъюнкции; символ квантора общности; символ квантора существования. Каждому функциональному символу и каждому символу отношения ставится в соответствие натуральное число - ранг данного символа. 1.2. Языки первого порядка. В общем случае язык первого порядка является набором из четырех множеств [3]. L=< Srt, Cnst, Fn, Pr>, котрый называется сигнатурой языка. В этом наборе 1) Srt - непустое множество, элементы которого называются сортами объектов. Для каждого сорта фиксируется счетный набор символов, которые называются переменными данного сорта. Среди логико-математических языков выделим односортные языки, в которых все предметные переменные имеют один сорт. Таков язык, например, арифметики. Напротив, язык линейной алгебры является двусортным (числа и векторы). Введение сортов позволяет потенциально рассматривать объекты разного рода. 2) Cnst - множество (может быть, и пустое) констант.Каждой константе языка приписывается определенный сорт Srt. Константы различных сортов различны. 3) Fn - множество (может быть, и пустое), элементы которого называются функциональными символами языка L (функциональными буквами). С каждой функциональной буквой однозначно связан некоторый объект - вид данной функциональной буквы. Вид функциональной буквы f есть выражение (1,…,k), где i, - сорта языка, k>0. Число k называется количеством аргументных мест символа f . Сорт i называется сортом i-го аргументного места символа f . В случае односортного языка для задания вида функционального символа достаточно указать количество его аргументов. 4) Pr - непустое множество, элементы которого называются предикатными символами (предикатными буквами) языка L. С каждой предикатной буквой P Pr связан некоторый обеъкт - вид данной предикатной буквы. Вид предикатной буквы P есть выражение вида (1,…,k), где i, есть сорт языка, k 0. Число k называется количеством аргументных мест символа P. Нульместные предикатные символы называются пропозициональными переменными. Под предикатом понимают функцию от переменных пробегающих некоторую область , которая в случае класической логики принимает только два значения:0,1. В дальнейшем, если не оговорено специально, под языком первого порядка мы будем понимать односортный язык первого порядка. Отмеченными выражениями языка первого порядка являются термы и формулы. Термы - это имена предметов, формулы –высказывания о предмктах. В формальных языках выражения строятся по строго определенным правилам. Термы в односортном языке строятся индуктивно с помощью следующтх превил. Все переменные являются термами. Все константные символы являются термами. Если f n- местный функциональный символ и x1,x2,…xn-термы, то f(x1,x2,…xn)-терм. При построении формул используются кроме перечисленных символы, которые называются логическими символами языка. Эти символы делятся на связки и кванторы. Определение. В формальном языке используются следующие логические связки: - конъюнкция, читается как “и”. - дизъюнкция, связка “или”. - импликация, “если…то”. -отрицание, связка “не”. Используются два квантора. - квантор всеобщности, читается как “для всех”.”для любого”. - квантор существования, “существует. Определение. Выражение вида P(t1,t2,…tn), где P n- местный предикатный символ, а t1,t2,…tn –термы называют атомарной формулой. Формулами являются выражения языка построенные по следующим правилам. Все атомарные формулы являются формулами. Если A и B формулы, то A B формула. Если A и B формулы, то A B формула. Если A и B формулы, то A B формула. Если A формула, то A формула. Если A формула и x произвольная переменная языка, то xA формула. Если A формула и x произвольная переменая языка, то xA формула. Определение. Терм не содержащий переменных называется замкнутым. Определение. Вхождение переменной в формулу называется связанным, если существует формула B, являющаяся частью исходной формулы C, содержащая данное вхождение переменной и такая, что B имеет вид xA илиxA. Определение. Формула не содержащая свободных вхождений переменных называтся замкнутой формулой или высказыванием.  Пример 1. Выделить связанные и свободные переменные в формуле x(P(y) F(x) xQ(x,z) xR(x,y)) Q(z,y). Пример 1. Выделить связанные и свободные переменные в формуле x(P(y) F(x) xQ(x,z) xR(x,y)) Q(z,y).Решение. Знак () x означает "квантор действует на переменную х", знак ' отмечает свободную переменную:    x(P(y') F(x) xQ(x,z') xR(x,y')) Q(z',y) Определение. Функциональной сложностью терма называют значение функции, заданной на множестве термов в соответствии со следующими правилами. 1. Если х переменная, то ῖ(x) = 0 2. Если х константа, то ῖ(x) = 0 3. Если терм имеет вид f(t1,...,tn), гдe t1,...,tn - термы, то ῖ(f(t1,...,tn)) = ῖ(t1)+...+ ῖ(tn)+1. Пример2. Для терма f(x,g(x,y),h(z) найти функциональную сложность. Решение. ῖ(f(x,g(x,y),h(z)) = ῖ(x)+ ῖ(g(x,y))+ ῖ(h(z))+1 = 0+ ῖ(x)+ ῖ(y)+1+ ῖ(z)+1+1 = 3 Определение. Логической сложностью формулы А называют значение функции l, определенной на множестве формул в соответствии со следующими правилами. 1.Если А - атомарная формула, то l(A) = 0. 2. l(A) = l(A)+1. 3. l(AB) = l(A)+l(B)+1. 4. l(AB) = l(A)+l(B)+1. 5. l(A B) = l(A)+l(B)+1. 6. l(xA) = l(A)+1 7.l(xA) = l(A)+1. Пример3. Вычислить логическую сложность формулы P((QR) (RP)) , гдe P,Q,R - атомарные формулы. Решение. l(P((QR) (RP))) = l(P)+l((QR) (RP))+1 = l((QR)+l(RP))+1+1 = l(Q)+l(R)+1+l(R)+l(P))+1+1+1 = 1+l(P)+1+1+1+1 = 5/ Задания . 1. Выписать все подформулы приведенных формул: a). Q(f(x),g(x,y)) P(x,y); б). (P (QR)) ((PQ) R); в). x(P(f(x)) yR(x,y)) Q(z,y); г). (R P) ((QR) P); д). (P Q) ((PQ) P). 2.Выделить связанные и свободные вхождения переменных в следующих формулах: a). x(A(x) B(x)) (xA(x) xB(x)); б). xy((F(y,z) F(x,z)) F(x,x) F(y,x))); в). (x(A(x) (B C(y)) x(A(x) Q(x,z))) P(x). 3. Доказать, что функциональная сложность терма равна числу вхождений в него функциональных символов. 4. Вычислить логическую сложность формул: a). ((P(QR))) ((PQ) R); б). ((P Q) (R P)) (Q R); в). Q(x,x) R(f(y,x)); г). (P (PQ)) (P ((PQ))); д). z(P(z) M ╞ А zQ(x,z) (yR(z,y)) Q(z,x). 5.Индукцией по построению термрв доказать, что для каждого терма t значение функциональной сложности l(t) равно количеству вхождений в терм функционального символа. 6.Индукцией по построению множества формул доказать, что l(А) равно количеству вхождения логических символов в формулу. 3.Семантика языка первого порядка и его интерпретация. Модели. Для придания смысла формулам формального языка, необходимо определить множество, элементы которого сопоставляются переменным языка. Пусть L язык первого порядка: L = < Srt, Cnst, Fn, Pr>. L = < D, Cnst, Fn, Pr>.-односортный язык. Тогда множество, элементы которого сопоставляются переменным языка L вводится следующим определением. Определение. Носителем языка L или объектной областью языка L называют функцию D, которая сопоставляет каждому сорту Str непустое множество D, D: → D. Можество D называют объектной областью сорта . Формулу языка, в которой вместо параметров подставлены элементы носителя называется оцененной и задает конкретное высказывание истинное или ложное при данных значениях (оценках) параметров. В случае односортного языка D совмадает с носителем. Формула языка, в каторой вместо параметров подставлены элементы носителя, называется оцененной, и задает конкретное высказывание, истинное или ложное при данных значениях (оценках) параметров. Каждая такая формула задает конкретное высказывание в модели. 3.1. Оценка термов и формул. При оценке формулы (терма) каждая переменная хi этой формулы заменяется на элемент носителя di. Так как при подстановке каждая переменная заменяется на конкретный элемент носителя, то оценка является константной подстановкой. Если Т - выражение языка L, то оценку обозначают символом , а оцененное выражение T. Каждый замкнутый терм в языке с носителем D определяет некоторый элемент этого носителя, а каждое высказывание языка является ложным или истинным утверждением об элементах носителя. Пусть t - замкнутый терм языка L. Значение tM терма, оцененного в модели M, определяется индукцией по построению термов [4], [5]. 1. Если с - константа из множества Const, то cM = č, гдe č - элемент носителя D, соответствующий константному символу с языка L. 2. Если t- переменная языка L, которой в интерпретации соответствует элемент d носителя D, то tM = d. 3. Если терм имеет вид f(t1,...,tn), то оценка терма определяется как f(t1,...,tn)M = f(t1M,...,tnM) . 4.Если t- терм языка L, содержащий параметры, то для всякой оценки Ø оцененный терм обозначается tØ, оценка которого tØ, т.е. терм с параметрами является функцией своей оценки. Оценку формул определяют рекурсией по длине формул [4]. Этой четверкой функций определяется модель М языка L. Т.е. модель есть "предписание" сопостовляющее символам языка объекты: функциональным символам - функции, предикатным символам - предикаты и т.д.Модель "наполняет" определенным содержанием символическое выражение языка, определяет его семантику.(в частности классическую семантику первого порядка - для языка первого порядка). Пример 4. Пусть задан терм t = (x+y)·z+x·y , гдe функциональным символам x+y,x·y приписаны функции (операции) сложения и умножения в множестве натуральных чисел N = {1,2,...}. Тогда терм t, оцененный посредством подстановки x=2, y=4 z=7, задает оцененный терм (2+7)·7+2·4, который имеет в N значение 64. Оцененные формулы языка в классической логике разделяются на истинные и ложные. Запись M ╞ A означает, что оцененная формула А истинна в модели М. Истинность оцененных в модели формул определяется индукцией по построению формул. M ╞ P(t1,...,tn) тогда и только тогда, когда Р(t1M,...,tnM) = 1 M ╞ A тогда и только тогда, когда неверно, что M ╞ А. M ╞ АВ тогда и только тогда, когда M ╞ А или M ╞ В. M ╞ АВ тогда и только тогда, когда M ╞ А и M ╞ В. M ╞ А В тогда и только тогда, когда если M ╞ А, то M ╞ В. M ╞ xA тогда и только тогда, когда d D, M ╞ A(xd), где A(xd) означает замену переменной х в формуле А на элемент носителя d. M ╞ xA тогда и только тогда, когда xA, M ╞ A(xd). Истинность или ложность формулы зависящей от параметров зависит от оценки параметров. Определение. Формальной аксиоматической теорией называют упорядоченную пару: T = Где L- логико-математический язык, X- некоторое множество предложений (замкнутых формул) языка L, которое называют множеством нелогических аксиом теории T. Пример 5. Пусть M = Решение. а). Наличие трех переменных не означает, что все переменные различны, то есть среди переменных в S3 могут оказаться одинаковые. б). Четность натурального числа у озачает, что найдется такое натуральное число х, что у является результатом сложения этого числа с самим собой, то есть у = х+х. Таким образом, имеем "у - четное число "= xS(x,x,y). Пример 6. Доказать, что формула xA(х) xA(х) является тавтологией. Решение. Необходимо доказать, что при любой оценке в модели М: M ╞ xA(х) xA(х). а). Переменная х не входит свободно в рассматриваемую формулу, поэтому область определения оценки Ø не включает переменную х, хотя она может входить свободно в формулу А. б). В связи с этим необходимо доказать, что : M ╞ x(AØ) x(AØ), где АØ - оцененная в модели М формула А. в). Допустим, что M ╞ x(AØ). Отсюда следует, что неверно M ╞ x(AØ); таким образом, для любого элемента d носителя модели М неверно M ╞ (AØ)(xd) и следовательно, каково бы ни было dD, M ╞ (AØ)(xd) - что в соответствии с истинностью дает M ╞ x (AØ) и, следовательно, M ╞ x(AØ). Задачи. 1. Доказать тождественную истинность формул: а). xA(х) xА(х); б). xуА(х,у) уxА(х,у). 2. Доказать, что если А не содержит свободно х, то: а). А xВ(х) x(АВ(х)); б). А xВ(х) x(АВ(х)); в). А xВ(х) x(АВ(х)); г). А xВ(х) x(АВ(х)); д). xВ(х) А x(В(х) А). Знак означает эквивалентность формул. Элементы теории моделей Def. 1. Множество 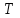 формул языка формул языка 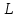 совместно, если совместно, если 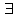 его модель, т.е. если его модель, т.е. если 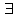 интерпретация языка интерпретация языка 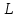 , в которой истинны все формулы из , в которой истинны все формулы из 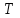 . .Таким образом, совместность понятие семантическое. Для одной и той же теории 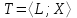 возможно возможно 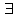 различных моделей, одну из которой называют стандартной. различных моделей, одну из которой называют стандартной.Def. 2. Две интерпретации некоторого языка одной и той же теории, в которых истинны одни и те же закрытые формулы, называются элементарно эквивалентными. Справедлива лемма: Лемма 1. Пусть 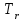 - множество всех закрытых формул языка - множество всех закрытых формул языка 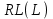 истинных в его стандартной интерпретации, тогда все формулы языка истинных в его стандартной интерпретации, тогда все формулы языка 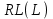 , не входящие в , не входящие в 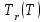 будут ложны в любой интерпретации (модели). будут ложны в любой интерпретации (модели).Д-во. Пусть 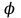 - закрытая формула, не входящая в - закрытая формула, не входящая в 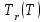 , тогда , тогда 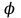 ложна в стандартной интерпретации (см. оценка терминов и формул в интерпретации Колмогоров.Др.). Тогда отрицание ложна в стандартной интерпретации (см. оценка терминов и формул в интерпретации Колмогоров.Др.). Тогда отрицание 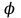 , т.е. , т.е. 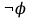 - истинно в стандартной интерпретации, следовательно - истинно в стандартной интерпретации, следовательно 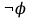 - истинно и в любой модели теории - истинно и в любой модели теории 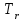 , а значит , а значит 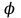 ложна в любой модели ложна в любой модели 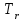 . Таким образом, в любой модели теории . Таким образом, в любой модели теории 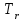 истинны те и только те (закрытые?) формулы, которые истинны в стандартной модели. истинны те и только те (закрытые?) формулы, которые истинны в стандартной модели.Теорема компактности Мальцева-Геделя. Пусть имеется произвольный язык 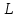 и произвольное множество и произвольное множество 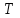 закрытых формул этого языка. Пусть также каждое конечное подмножество закрытых формул этого языка. Пусть также каждое конечное подмножество 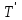 множества множества 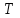 совместно, тогда и все множество совместно, тогда и все множество 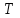 совместно. совместно.(Истинность для д-ва т. направленности) Д-во. (стр. 73, далее д-в) В соответствии с теоремой Геделя-Мальцева о полноте совместность множества формул эквивалентна с непротиворечивостью, таким образом достаточно доказать, что если всякое конечное подмножество данных формул непротиворечиво, то и все множество формул 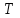 непротиворечиво. непротиворечиво. 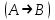 Или: 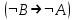 Если противоречиво данное множество 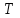 , то противоречиво и некоторое его конечное подмножество. , то противоречиво и некоторое его конечное подмножество.Это следует из свойства выводимости. 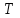 противоречиво противоречиво 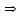 из из 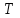 ├ ├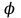 и и 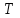 ├ ├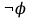 , тогда (по свойству выводимости) найдутся конечные множества , тогда (по свойству выводимости) найдутся конечные множества 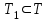 ; ; 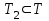 , что из , что из 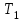 ├ ├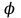 , а из , а из 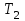 ├ ├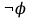 , тогда из конечного множества , тогда из конечного множества 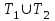 ├ ├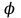 ; ; 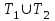 ├ ├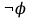 и следовательно конечное множество и следовательно конечное множество 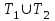 - противоречиво. - противоречиво.Лемма 2. Если формула 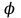 выводится из множества формул выводится из множества формул 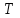 , то , то 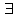 конечное подмножество конечное подмножество 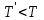 такое, что такое, что 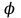 выводится из выводится из 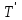 . .Def. 2. Множество формул 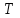 противоречиво, если из него выводится некоторая формула противоречиво, если из него выводится некоторая формула 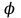 и ее отрицание и ее отрицание 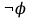 . .Теорема Геделя-Мальцева (стр. 734). Пусть 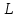 - произвольный язык (одное. яз. 1-го пор.), - произвольный язык (одное. яз. 1-го пор.), 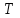 - множество закрытых формул этого языка. Тогда равносильны следующие утверждения: - множество закрытых формул этого языка. Тогда равносильны следующие утверждения:а) 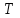 совместно (т.е. совместно (т.е. 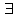 модель – семантическое св-во) модель – семантическое св-во)б) 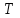 непротиворечиво (т.е. выводится непротиворечиво (т.е. выводится 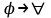 , т.е. …. (далее см. со стр. 78). , т.е. …. (далее см. со стр. 78).(Искать приемлемое доказательство) Т.е. теорема утверждает эквивалентность семантического критерия синтаксическому. !!! Приведенные утверждения математической логики позволяют обосновать возможность построения н/с модели (интерпретации) теории функцией действительного переменного, так называемой н/с анализ, в котором наряду с обычными 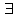 бесконечно малые и бесконечно большие числа. бесконечно малые и бесконечно большие числа.Будем рассматривать язык 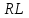 , содержащий функциональные символы для каждой функции с действительными аргументами и значениями. Тогда наша задача может быть сформулирована так: доказать , содержащий функциональные символы для каждой функции с действительными аргументами и значениями. Тогда наша задача может быть сформулирована так: доказать 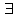 интерпретации языка интерпретации языка 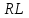 , в которой истинны те же закрытые формулы языка 1-го порядка, что и в стандартной интерпретации, но носитель которой включает бесконечно малые величины. Эту интерпретацию назовем гипердействительной, стандартную – действительной. , в которой истинны те же закрытые формулы языка 1-го порядка, что и в стандартной интерпретации, но носитель которой включает бесконечно малые величины. Эту интерпретацию назовем гипердействительной, стандартную – действительной.Замечание. Стандартные действительные числа удовлетворяют аксиоме Архимеда: 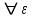 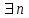 т.ч. т.ч. 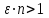 или или 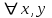 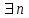 т.ч. т.ч. 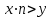 и тогда не и тогда не 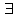 бесконечно малых чисел, т.к. если бесконечно малых чисел, т.к. если 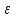 - бесконечно малое, то - бесконечно малое, то 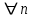 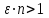 . .Не противоречит ли это нашему требованию об истинности одних и тех же закрытых формул 1-го порядка в обеих интерпретациях? Аксиома Архимеда имеет вид: 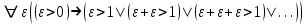 Эта бесконечная формула 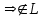 Если 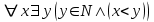 , то в новой интерпретации она может быть верна, но в ней , то в новой интерпретации она может быть верна, но в ней  не обыкновенный счетный натуральный ряд, а содержит бесконечно большие числа. не обыкновенный счетный натуральный ряд, а содержит бесконечно большие числа.Утв. 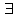 модель элементарно эквивалентная модель элементарно эквивалентная 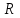 такая, что в такая, что в 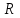 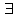 бесконечно малые величины. бесконечно малые величины.Д-во. Добавим к языку 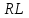 , содержащему все функциональные символы всех функций на , содержащему все функциональные символы всех функций на 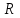 , еще один нульместный функциональный символ (константу) , еще один нульместный функциональный символ (константу) 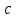 , отличный от всех имеющихся. Расширенный язык обозначим , отличный от всех имеющихся. Расширенный язык обозначим 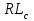 . Для того, чтобы задать стандартную интерпретацию, возьмем стандартную интерпретацию языка . Для того, чтобы задать стандартную интерпретацию, возьмем стандартную интерпретацию языка 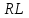 , выберем в ее носителе элемент и объявим его значением добавленного символа , выберем в ее носителе элемент и объявим его значением добавленного символа 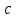 . Наоборот, если имеется некоторая интерпретация . Наоборот, если имеется некоторая интерпретация 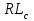 , интерпретацию , интерпретацию 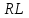 получим из нее просто исключить символ получим из нее просто исключить символ 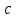 и то, какой элемент ему соответствует. и то, какой элемент ему соответствует.Рассмотрим множество закрытых формул 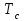 нового языка. Оно содержит: нового языка. Оно содержит:а) Все закрытые формулы 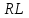 , истинные в стандартной интерпретации , истинные в стандартной интерпретации 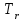 . .б) И кроме того, счетное множество формул вида: 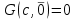 ; ; 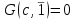 ; ; 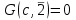 ; … ; …где 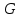 - двуместный функциональный (предикатный) символ, для которого - двуместный функциональный (предикатный) символ, для которого 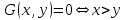 , а , а 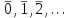 соответствуют нульместным функциональным символам языка соответствуют нульместным функциональным символам языка 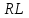 , соответствующим числам 0, 1, 2, … , соответствующим числам 0, 1, 2, …Достаточно показать, что 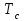 совместно (т.е. имеет модель) (тогда совместно (т.е. имеет модель) (тогда 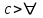 натурального числа). Но это следует из теоремы компактности. Действительно, выберем натурального числа). Но это следует из теоремы компактности. Действительно, выберем  конечное подмножество конечное подмножество 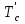 множества множества 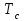 . Тогда . Тогда 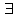 семейство формул семейство формул 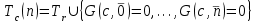 , которое при достаточно большом , которое при достаточно большом 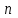 включает включает 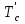 . .Если совместно 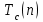 , то совместно и , то совместно и 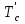 (в модели для (в модели для 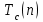 истинны все истинны все 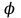 из из 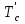 ). ).Для доказательства совместности 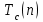 построим его модель. Для этого возьмем стандартную интерпретацию языка построим его модель. Для этого возьмем стандартную интерпретацию языка 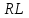 и расширим ее до интерпретации языка и расширим ее до интерпретации языка 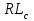 , считая, что , считая, что 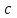 интерпретируется как число интерпретируется как число 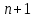 . Очевидно . Очевидно 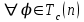 . . 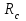 ╟ ╟ 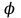 . .Таким образом, 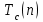 совместно совместно 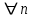 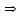 по теореме компактности совместно множество по теореме компактности совместно множество 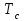 , модель этого множества формул , модель этого множества формул 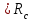 , превращается в искомую систему гипердействительных чисел , превращается в искомую систему гипердействительных чисел 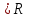 , как только будет «забыто» о , как только будет «забыто» о 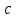 (т.е. исключить из языка (т.е. исключить из языка 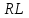 символ символ 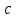 , а в интерпретации , а в интерпретации 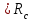 забыть о том, что элементу забыть о том, что элементу 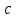 приписан соответствующий символ). приписан соответствующий символ).Таким образом, в 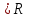 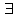 бесконечно большие бесконечно большие 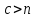 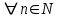 , следовательно , следовательно 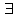 и бесконечно малые, например, и бесконечно малые, например, 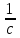 . . |
