Логика как наука, практическое значение логики Логика происходит от греческого слова logos, что значит мысль, слово, разум

• Название: Логика как наука, практическое значение логики Логика происходит от греческого слова logos, что значит мысль, слово, разум
• Дата: 28.04.2022
• Размер: 258.17 Kb.
• Имя файла: 24.docx
• Тип: Закон; #502890

1. 
   Логика как наука, практическое значение логики
   

«Логика» происходит от греческого слова logos , что значит «мысль, слово, разум». Наука о мышлении. Предметом изучения логики являются формы и законы правильного мышления. 

Логика как одна из наук о мышлении, философски окрашенная наука. Это -- наука о структуре форм мысли, о простейших мыслительных методах, о законах связи форм мысли между собой, а также и об ошибках, возможных при нарушении этих законов.

Практическое значение логики:

Логика дает человеку способность обосновывать, возможность корректно доказывать и успешно убеждать. Логика выводит рассуждения на уровень строгой теории.

1) Логика указывает на ошибки в мыслительной деятельности (Все, имеющие конспекты, получат зачет. Значит, не имеющие конспектов не могут рассчитывать на зачет? Конечно, не значит.)

2) Прояснение логической интуиции (ср.: мы правильно говорим, но не отказываемся от грамматики).

3) Логика формирует культуру мышления (четкость, последовательность, доказательность рассуждения; усиление эффективности и убедительности речи; формирование умения выделять главное, ясность и трезвость мысли). 

2. 
   История развития логики
   

Принято именно Аристотеля (384—322 до н.э.) считать отцом логики, хотя Аристотель, как известно, учился у Пла­тона, Платон — ученик Сократа, а Сократ большую часть своей долгой жизни потратил на разоблачение псевдо­учености софистов, которые до него уже исследовали вопросы языка и мышления. 

Историю логики можно разделить на два основных этапа: первый продолжался более двух тысяч лет, в течение которых логика развивалась очень медленно; второй начался во второй половине XIX в., когда в логике произошла научная революция, в корне изменившая ее лицо. Это было обусловлено прежде всего проникновением в нее математических методов. На смену аристотелевской, или традиционной, логике пришла современная логика, называемая также математической, или символической. Эта новая логика не является логическим исследованием исключительно математических доказательств. Она представляет собой современную теорию правильного рассуждения, «логику по предмету и математику по методу», как охарактеризовал ее известный русский логик П.С.Порецкий. Таким образом, по Аристотелю, предмет науки логики — основные формы мысли, их структурные особенности и зависи­мости, законы и наиболее распространенные ошибки, возможные при нарушении этих законов.

3. 
   Основные логические законы
   

Логика выделяет четыре основных свойства логического мышления.

Это законы тождества, непротиворечия, исключенного третьего и достаточного основания. Они действуют в любом рассуждении, в какой бы логической форме оно ни протекало и какую бы логическую операцию ни выполняло. 

1. 
   Закон тождества. Любая мысль в процессе рассуждения должна сохранять одно и
   

то же содержание или смысл, сколько бы она не повторялась. Каждое понятие должно употребляться в одном и том же смысле. Всякая мысль в процессе

рассуждения должна быть тождественна самой себе(А есть А, или А=А, где под А понимается любая мысль). (Убеждение существует. Убеждение не существует.)

2. Закон непротиворечия. Логическое мышление характеризуется непротиворечивостью.

Два несовместимых друг с другом суждения не могут быть одновременно истинными; одна из них необходимо является ложь.

Этот закон формулируется следующим образом: неверно, что А и не - А(не могут быть истинными две мысли, одна из которых отрицает другую). Где А – произвольное высказывание, выражающее любую мысль.

Закон непротиворечия действует в отношении всех несовместимых суждений.

2. 
   Закон исключенного третьего. Закон противоречия выражает ту закономерность,
   

что две таких мысли не могут быть одновременно истинными, одна из них необходимо ложна. Формула: А или не – А, где А – любое суждение. Например «Дождь идет» или «Дождь не идет».

Закон исключенного третьего действует только в отношении противоречащих (контрадикторных) суждений.

3. 
   Закон достаточного основания.Выражает черту правильного мышления.
   

Любая мысль должна быть доказана другими мыслями, истинность которых доказана ранее.

Если из истинности суждения а следует истинность суждения b, то а будет основанием для b, a b — следствием этого основания.

4. 
   Понятие как форма мысли
   

Понятие – это мысль о существенных признаках предметов.

Выделяют 2 типа:

1. 
   необходимые – признаки неотчуждаемые от феномена (что неизбежно)
   
2. 
   случайные – признаки происходящие (может произойти, а может и не произойти)
   

Структура понятия включает два элемента: 1) содержание, 2) объём.

Содержание понятия – это совокупность признаков присущих объему. (Например, студент - все те предметы, для которых характерны признаки "быть учащимся" и "учиться в высшем учебном заведении". Объем понятия "простое число" – это множество чисел, каждое из которых делится на единицу или на самое себя, т.е. это числа 1, 2, 3, 5, 7, и т.д)

Объём понятия – это множество предметов, которое мыслится в понятии. (Например, человек – это существо, наделенное разумом, волей, чувствами, имеющим широкие ногти, два глаза и т.п)

Связь между содержанием и объёмом понятия выражается в логическом законе обратного отношения между ними, который можно сформулировать так: пусть имеются два понятия, содержание одного из которых меньше содержания другого, тогда объём первого больше объёма второго.

5. 
   Объём и содержание понятия
   

Содержание понятия  - это совокупность признаков присущих объему. (Например, студент - все те предметы, для которых характерны признаки "быть учащимся" и "учиться в высшем учебном заведении". Объем понятия "простое число" – это множество чисел, каждое из которых делится на единицу или на самое себя, т.е. это числа 1, 2, 3, 5, 7, и т.д)

Объем понятия это множество предметов, которое мыслится в понятии. (Например, человек – это существо, наделенное разумом, волей, чувствами, имеющим широкие ногти, два глаза и т.п)

6. 
   Операции обобщения и ограничения
   

Обобщение понятий – есть процесс перехода от понятия с меньшим объемом, но большим содержанием к понятию с большим объемом, но меньшим содержанием. Например, обобщая понятие «хвойный лес», мы переходим к понятию «лес». Содержание уменьшилось, объем стал шире.

Ограничение понятий – операция обратная. С большим объемом, но меньшим содержанием к понятию с меньшим объемом, но с большим содержанием. Например, понятие «юрист», добавить характеризующийся признак, то получим новое понятие «юрист-криминолог».

7. 
   Операция определения
   

Определение понятий – операция по прояснению содержания понятия:

- определяемое -

- определяющее – которое позволяет узнать

Правила определения:

1. 
   Определение должно быть соразмерным – объем определяемого и определяющее должно иметь тождество, т.е находится в равнообъемности
   
2. 
   Определение должно быть ясным
   
3. 
   Определение не должно содержать кольца, когда в определяемом есть такие слова, как и в определяющем
   
4. 
   По возможности определение не должно быть отрицательным.
   

Остенсивное определение – определение по средствам указания.

Определения делятся на 1) номинальные и реальные, 2) явные и неявные.

Реальные – определения, раскрывающие содержание

Номинальные – вводится новый термин (имя), объясняется значение термина, его происхождение и т.п. (вещественное доказательство - «улика»)

Явные – между определяемым и определяющим устанавливается равенство (т.е сначала указывается родовой признак, затем выделяется вид)

Неявные – определения, где содержание раскрывается косвенным путём.

8. 
   Операция деления
   

Деление понятий – операция по прояснению объема понятий.

1. 
   Делимое – понятие, которое делят
   
2. 
   Подмножества делений – видовые понятия по отношению к исходному
   
3. 
   Основание деления – признак, по которому происходит деление
   

Правила деления:

1. 
   Деление должно быть соразмерным
   
2. 
   Основание деления должно быть неизменным
   
3. 
   Подмножество деления не должны пересекаться в объеме
   
4. 
   Деление должно быть непрерывным
   

В логике принято различать два вида деления:

─ видовое деление;

─ дихотомическое.

Видовое деление – основанием является признак, принадлежащий всем предметам. (на полу делят на мужчин и женщин)

Дихотомическое - где основанием является признак, принадлежащий некоторым предметам.

9. 
   Виды понятий
   

Классификация по объему:

1. 
   Общие – весь возможный объем (страна, писатель)
   
2. 
   Частные – только часть возможного объема
   
3. 
   Единичные – объем которых равен 1 (Лондон)
   
4. 
   Нулевые – объем которых равен 0. (преступник, не совершавший преступление)
   

Классификация понятий по содержанию:

1. 
   Утвердительные – наличие некого признака (грамотный человек)
   
2. 
   Отрицательные – отсутствие признака (не говорящий по английски)
   

Понятия:

1. 
   конкретные – обозначают предмет (существа, продукт, вещи)
   
2. 
   абстрактные – обозначают признаки предметов (твердость, долговечность)
   

10. 
    Круги Эйлера
    

Понятия по характеру отношений между их объёмами делятся:

1. 
   Совместимые - когда элементы объёма одного понятия частично или
   

полностью принадлежат объёму другого понятия

2. 
   Несовместимые - когда ни один элемент объёма одного понятия не
   

принадлежит объёму другого понятия).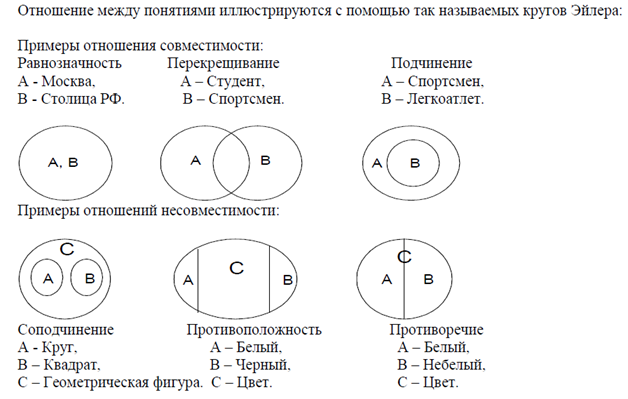

11. 
    Суждение как форма мысли
    

Суждение - это форма мышления, в которой утверждается или отрицается связь между предметом и его признаком, отношения между предметами или факт существования предметов; суждение может быть либо истинным, либо ложным.

12. 
    Виды суждений
    

По количеству:

1. 
   Простые – один субъект или один предикат
   
2. 
   Сложные – более одного субъекта и/или предиката
   

Качество суждения — разумеется не фактическое содержание суждения, а его самая общая логическая форма — утвердительная или отрицательная.

Количество суждения — подразумевает характер субъекта, т.е. его логический объем. (Например, число дней недели, месяцев или времен года) В зависимости от этого выделяются общие, частные и единичные суждения.

1. 
   Единичноутвердительные: s есть P. Александр Пушкин – это русский писатель.
   
2. 
   Единичноотрицательные: s не есть P. Сервантес не был художником.
   
3. 
   Общеутвердительные: Все S есть P. Все квартиры в этом доме имеют высокие потолки.
   
4. 
   Общеотрицательные: Ни один S не есть P. Ни один студент из нашей группы не сдал экзамен на пятёрку.
   
5. 
   Частноутвердительные: Некоторые S есть P. Некоторые машины из нашего автопарка нуждаются в срочном ремонте.
   
6. 
   Частноотрицательные: Некоторые S не есть P. Некоторые тексты песен не имеют смысла.
   

13. 
    Структура простого суждения
    

1. 
   Субъект – фрагмент действительности, описываемый суждением. Москва
   
2. 
   Предикат – совокупность признаков, приписываемые субъекту. Столица России
   
3. 
   Связка – элемент суждения, обеспечивающий взаимодействие субъекта и предмета.
   
4. 
   
   

14. Логическое значение простого суждения

Логическое значение суждение – честность или ложность суждения.

14. 
    Квадрат истинности
    

А 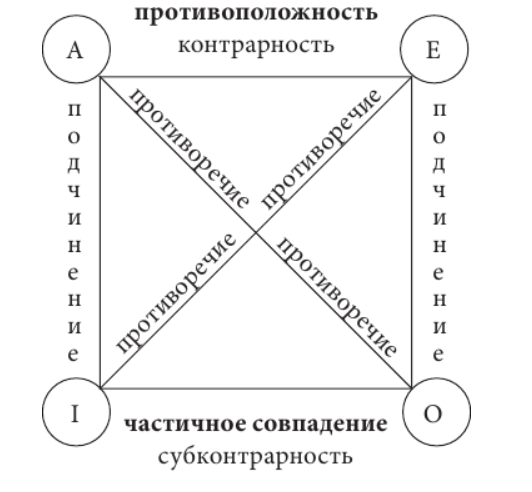-общее утверждение суждения

Все S являются P

I – частное-утвержденные суждения

Некоторые S являются P

E – Общее отрицательные суждения

Ни одно S являются P

O – частное -отрицательное

Некоторые S являются P

16. Распределённость терминов в суждениях.

Термин считается распределенным, если он взят в полном объеме. Термин считается нераспределенным, если он взят в части объема.

Суждение А (Все S являются P). «Все студенты нашей группы (S) сдали экзамены (Р)»

Суждение Е (Ни одно S не есть Р). «Ни один студент нашей группы (S) не является неуспевающим (Р)».

Суждение I (Некоторые S суть Р). «Некоторые студенты нашей группы (S) – отличники (Р)».

Суждение О (некоторые S не суть Р). «Некоторые студенты нашей группы (S) – не отличники (Р)».

17.Структура сложного суждения.

Сложное суждение – суждение, состоящее из нескольких простых суждений, связанных между собой логическими союзами.

18. Логическое значение сложного суждения. Таблицы истинности.

Конъюнкция– логическая операция, по смыслу максимально приближенная к союзу «и». Конъюнкция будет истинной при истинности всех ее суждений.

Р	Q	P ˄ Q
И	И	И
И	Л	Л
Л	Л	Л
Л	И	Л

Дизъюнкция – логическая операция, по применению максимально приближенная к союзу «или». Дизъюнкция будет истинной при истинности, хотя одного суждения.

P	Q	P˅Q
И	И	И
И	И	И
Л	И	И
Л	Л	Л

Строгая дизъюнкция – логическая операция, оператор условия (если Р, то Q). Будет истинной при разных логических значениях ее суждений. Импликация будет истинной при выполнении, хотя одного из двух условий:

1. 
   Антецедент (первая часть условия) не верен;
   
2. 
   Консеквентен (последствия) верен.
   

Р	Q	P ˅Q
И	И	Л
И	Л	И
Л	И	И
Л	Л	Л

Эквиваленция– логическое выражение, которое является истинным тогда, когда оба простых логических выражения имеют одинаковую истинность.

P	Q	P <=>Q
И	И	И
И	Л	Л
Л	И	Л
Л	Л	И

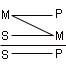
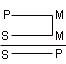
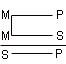
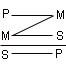
19. Модальные суждения: суть, виды.

Модальность – это явно или неявно выраженная в суждении дополнительная информация о логическом или фактическом статусе суждения, о регулятивных, оценочных, временных и других его характеристиках.

Алетическая модальность выражает характер связи между мыслимыми предметами, между субъектом и предикатом. (Возможно, случайно)

Деонтическая модальность распространяется на деятельность людей, нравственные и правовые нормы их поведения в обществе. (Разрешается, запрещается, обязательно)

Эпистемическая модальность характеризует степень достоверности знания (Доказано, недоказуемо, опровергнуто)

Аксиологическая модальность выражает отношение человека к материальным и духовным ценностям (хорошо, плохо)

20. Умозаключение как форма мысли.

Умозаключение – это форма мышления, посредством которой из одного или нескольких суждений выводится новое.

Элементы:

Посылки– суждения истинностью, которых мы руководствуемся.

Заключение­– суждения в результате процедуры умозаключения.

Вывод– процесс перехода от посылок к заключению.

21. Виды умозаключений.

Дедуктивные – умозаключения, в которых из общего правила делается вывод для частного случая. (Все звезды излучают энергию. Солнце – это звезда. Солнце излучает энергию)

Индуктивные – умозаключения, в которых из нескольких частных случаев выводится общее правило. (Юпитер движется. Марс движется. Венера движется. Юпитер, Марс, Венера – это планеты. Все планеты движутся)

Умозаключения по аналогии – умозаключения, в которых на основе сходства предметов (объектов) в одних признаках делается вывод об их сходстве и в других признаках. (Планета Земля расположена в солнечной системе, на ней есть атмосфера, вода и жизнь. Планета Марс расположена в солнечной системе, на ней атмосфера и вода. Вероятно, на Марсе есть жизнь)

22. Непосредственные умозаключения.

Суждение, содержащее новое знание, может быть получено посредством преобразования суждения. Так как исходное (преобразуемое) суждение рассматривается как посылка, а суждение, полученное в результате преобразования, – как заключение, умозаключения, построенные посредством преобразования суждений, называются непосредственными.

23.Структура простого категорического силлогизма.

Простой категорический силлогизм состоит из трех простых суждений (посылок и заключений).

Термины:

S – меньший термин, субъект заключения

P – большой термин, предикат заключения

M – средний термин, входит в обе посылки, но не входит в заключение.

Посылки:

Большая посылка – посылка, содержащая Р – предикат заключения, записывается первой.

Меньшая посылка – посылка, содержащая S – субъект заключения, записывается второй

(Всякий человек смертен. Сократ– человек. Сократ смертен.)

24. Правила простого категорического силлогизма.

Правило 1.  Терминов должно быть только три

В каждом силлогизме должно быть только 3 термина (S, Р. М).Если правило нарушено, то ошибка называется «учетверение термина». Эта ошибка основана на нарушении требований закона тождества и называется учетверением терминов.

Пример такой ошибки

: Труд — основа жизни.

Изучение логики — труд.

Изучение логики — основа жизни.

Здесь термин «труд» трактуется в разном смысле: в большей посылке — широко, а в мень­шей — узко.

Правило 2. Средний термин должен быть распределен хотя бы в одной из посылок.

Если средний термин не распределен ни в одной из посылок, то отношение между крайними терминами в заключении остается неопределенным.

Духи «Шанель» имеют приятный запах.

Духи «Шанель» полезны.

Здесь средний термин «имеют приятный запах» (удобно записывать так: «есть имеющие приятный запах») не распределен ни в одной из посылок. Поэтому заключение ложно.

Правило 3. Термин, не распределенный в посылках, не может быть распределен в заключении.

Распределенность крайних терминов в посылках и в заключении должна быть одинаковой. При нарушении этого правила возникает логическая ошибка «незаконное расширение термина».

Все солдаты умеют стрелять.

Все дети—не солдаты.

Все дети не умеют стрелять.

Предикат вывода («умеют стрелять») — распределен, а в посылке он не распределен. Смысл этого правила состоит в том, что при его нарушении в заключении о большем круге предметов, чем содержится в посылках.
25.Фигуры и модусы простого категорического силлогизма

Фигуры силлогизма- это его разновидности, различающиеся положением среднего термина (М) в посылках. Существует 4 разновидности:   

1. 
   средний термин занимает место субъекта в большей посылке предиката в меньшей
   
2. 
   средний термин занимает место предиката в обеих посылках
   
3. 
   средний термин занимает место субъекта в обеих посылках.
   
4. 
   средний термин является предикатом в большей посылке и субъектом в
   

меньшей

1-я фигура	2-я фигура	3-я фигура	4-я фигура

1. 
   Все металлы (М) - электропроводны (Р) Медь (S) - металл (М). Медь (S) –
   

электропроводна (Р)

2. 
   Этот смертельный удар (Р) нанесен человеком огромной силы (M) Обвиняемый (S)
   

Не является человеком огромной силы (М). Обвиняемый (S) не нанес этот смертельный удар (P)

3. 
   Ни один страус (М) не летает (Р) Все страусы (М) птицы (S). Некоторые птицы (S)
   

Не летают (P)

4. 
   Ни один счастливый человек(Р) не стремится к справедливости (М) Некоторые
   

стремящиеся к справедливости люди (M) являются юристами (S).

Фигура силлогизма называется модусами.

Модусы фигуры отличаются друг от друга качественной и/или количественной характеристиками входящих в них суждений.

Количество модусов у каждой фигуры – 64, а всего модусов четырех фигур насчитывается 256. Однако большинство из них не являются правильными, поскольку могут приводить от истинных посылок к ложному заключению.

26.Чисто условные умозаключения

Чисто условным называется умозаключение, обе посылки которого являются условными суждениями.  

Если у преступника был сообщник(p), то на лицо преступная группа(q), а если преступление совершено группой, то это — преступление с отягчающими обстоятельствами(r). Значит, если у преступника был сообщник, то это — преступление с отягчающими обстоятельствами(r).

Следует, что обе посылки – условные суждения, причем следствие первой посылки является основанием второй (q), из которого, в свою очередь, вытекает некоторое следствие (r). Общая часть двух посылок (q)  позволяет связать основание первой (р) и следствие второй (r). Поэтому заключение также выражается в форме условного суждения.

Схема чисто условного умозаключения:
(p → q)  ∧ (q →  r),
(Р → r).

Вывод: следствие следствия есть следствие основания

Умозаключение, в котором заключение получается из двух условных посылок, относится к простым.
Однако заключение может следовать из большего числа посылок, которые образуют цепь условных суждений. Такие умозаключения называются сложными.

27.Условно-категорические умозаключения

Условно-категорическим называется умозаключение, в котором одна из посылок — условное, а другая посылка и заключение — категорические суждения.

Это умозаключение имеет два правильных модуса: 1) утверждающий и 2) отрицающий.

1. 
   В утверждающем модусе - посылка, выраженная категорическим
   

суждением, утверждает истинность основания условной посылки, а заключение утверждает истинность следствия.

Если иск предъявлен недееспособным лицом (р), то суд оставляет иск без рассмотрения (q). Иск предъявлен недееспособным лицом (р) Суд оставляет иск без рассмотрения (q).

Схема модуса: p —> q, p

Первая посылка — условное суждение, выражающее связь основания (р) и следствия (q). Вторая посылка — категорическое суждение, в котором утверждается истинность основания (р): иск предъявлен недееспособным лицом. Признав истинность основания (р), мы признаем истинность следствия (q): суд оставляет иск без рассмотрения.

2. 
   В отрицающем модусе - посылка, выраженная категорическим суждением,
   

отрицает истинность следствия условной посылки, а заключение отрицает истинность основания.

Если иск предъявлен недееспособным лицом (р), то суд оставляет иск без рассмотрения (q). Суд не оставил иск без рассмотрения (не-q) Неверно, что иск предъявлен недееспособным лицом (не-р). 

Схема отрицающего модуса: p->q, —|q-p|

Достоверные заключения дают два: утверждающий и отрицающий. Они выражают законы логики и называются правильными модусами условно-категорического умозаключения. Эти модусы подчиняются правилу: утверждение основания ведет к утверждению следствия и отрицание следствия — к отрицанию основания.

28. Условно-разделительные умозаключения.

Условно-разделительное умозаключение, в котором одна посылка состоит из двух условных суждений, а другая являет­ся разделительным суждением.

1. 
   Конструктивная дилемма(простая) - условная посылка содержит два
   

основания, из которых вытекает одно следствие. Разделительная посылка утверждает оба возможных основания, заключение утверждает следствие.



Если обвиняемый виновен в заведомо незаконном задержании (р), то он подлежит уголовной ответственности за преступление против правосудия (r); если он виновен в заведомо незаконном заключении под стражу (q), то он также подлежит уголовной ответственности за преступление против правосудия (r). Обвиняемый виновен или в заведомо незаконном задержании (р), или в заведомо незаконном заключении под стражу (q).

Обвиняемый подлежит уголовной ответственности за преступление против правосудия (r).

2. 
   Конструктивная дилемма (сложная) условная посылка содержит два основания и
   

два следствия. Разделительная посылка утверждает оба возможных основания.

3. 
   Простая деструктивная дилемма - условная посылка содержит одно основание,
   

из которого вытекает два возможных следствия. Разделительная посылка отрицает оба следствия, заключение отрицает основание.



Если Н. совершил умышленное преступление (р), значит, в его действиях был прямой (q) или косвенный умысел (r).

Но в действиях Н. не было ни прямого (q), ни косвенного умысла (r). Преступление, совершенное Н., не является умышленным (р).

4. 
   Сложная деструктивная дилемма - условная посылка содержит два основания и
   

два следствия. Разделительная посылка отрицает оба следствия, заключение отрицает оба основания.

30. Разделительно-категорическое умозаключение.

Разделительно-категорическим называется умозаключение, в котором одна из посылок — разделительное, а другая посылка и заключение — категорические суждения.

Различают 2 модуса:

1. 
   Утверждающе-отрицательный модус меньшая посылка — категорическое
   

суждение — утверждает один член дизъюнкции, заключение — также категорическое суждение — отрицает другой ее член.  

Облигации могут быть предъявительскими (р) или именными (q). Данная облигация предъявительская (q).

Данная облигация не является именной (не-q).

Схема утверждающе-отрицающего модуса:

2. 
   Отрицающе-утверждающий модус - меньшая посылка отрицает один дизъюнкт,
   

заключение утверждает другой. 

Облигации могут быть предъявительскими (р) или именными (q). Данная облигация не является предъявительской (не-р). Данная облигация именная (q).

Схема отрицающе-утверждающего модуса:


, ?р

31. Индуктивное умозаключение.

Логический переход от знания об отдельных явлениях к знанию общему совершается в форме индуктивного умозаключения, или индукции.

Индуктивным называется умозаключение, в котором на основании принадлежности признака отдельным предметам или частям некоторого класса делают вывод о его принадлежности классу в целом.

Посылками индуктивного умозаключения выступают суждения, в которых фиксируется полученная опытным путем информация о повторяемости признака Р у ряда явлений – S1, S2, Sn, принадлежащих одному и тому же классу К.

Схема умозаключения имеет следующий вид:

В основе логического перехода от посылок к заключению в индуктивном выводе лежит подтверждаемое тысячелетней практикой положение о закономерном развитии мира, всеобщем характере причинной связи, проявлении необходимых признаков явлений через их всеобщность и устойчивую повторяемость. Именно эти методологические положения оправдывают логическую состоятельность и эффективность индуктивных выводов.

Основная функция индуктивных выводов в процессе познания – генерализация, т. е. получение общих суждений. По своему содержанию и познавательному значению эти обобщения могут носить различный характер – от простейших обобщений повседневной практики до эмпирических обобщений в науке или универсальных суждений, выражающих всеобщие законы.

Важное место принадлежит индуктивным выводам в судебно-следственной практике – на их основе формулируются многочисленные обобщения, касающиеся обычных отношений между людьми, мотивов и целей совершения противоправных действий, способов совершения преступлений, типичных реакций виновников преступления на действия следственных органов и т. п.

В зависимости от полноты и законченности эмпирического исследования различают два вида индуктивных умозаключений: полную индукцию и неполную. В неполной индукции различают популярную и научную в зависимости от способа отбора исходного материала. Научная индукция делится в зависимости от способа исследования на индукцию методом отбора и индукцию методом исключения.

32. Умозаключение по аналогии.

Основанием умозаключений по аналогии служит сходство (аналогия) предметов, их свойств и отношений. Сходство предметов определяется двумя факторами:

1) числом признаков, общих для этих предметов;

2) степенью существенности этих признаков.

Пример. Предметы «стул» и «письменный стол» имеют много общих признаков: это предметы мебели, они могут быть изготовлены из одного материала, могут иметь четыре ножки, всегда имеют плоскую горизонтальную поверхность и т.д. Однако все эти признаки, кроме признака «быть предметом мебели», являются несущественными. Зато стул и письменный стол отличаются своими существенными признаками: стул предназначен для сидения, стол – для письма; стул имеет спинку, стол не имеет и т.д. Таким образом, стол и стул похожи, по преимуществу, в несущественных признаках и различаются существенными. Следовательно, нельзя говорить о таком их сходстве, которое могло бы служить основанием выводов по аналогии.

Заключения аналогии не являются достоверно истинными при истинности посылок, а только вероятно истинными. Вероятность истинности заключений выводов по аналогии низка даже по сравнению с популярной индукцией. Поэтому в науке аналогия редко используется как средство обоснования или доказательства суждений.

Но умозаключения по аналогии играют важную эвристическую роль в научном познании. Аналогия – один из основных способов формирования научных гипотез, источник догадок и предположений, которые затем проходят проверку более строгими дедуктивными и индуктивными методами. На первых этапах исследования незнакомых явлений ученый ищет среди уже известных ему явлений какие-то аналогии для нового.

Помимо этого, умозаключения по аналогии - одна из составляющих метода моделирования. В силу использования умозаключений по аналогии результаты моделирования всегда носят вероятностный характер.

В умозаключениях по аналогии используются следующие понятия:

-          образец аналогии - объект, признак которого переносится на другой объект;

-          субъект аналогии - объект, на который переносится признак;

-          термины аналогии - это образец и субъект аналогии;

-          переносимый признак - признак, который переносится с образца на субъект;

-          основание аналогии - признак, одновременно присущий обоим терминам аналогии и служащий основанием для переноса интересующего нас признака.