ргр по теплопередаче. Ргр по тех тпелопередаче. М. А. Зырянов оценка подпись, дата инициалы, фамилия
 Скачать 106.97 Kb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «Сибирский государственный университет науки и технологий имени академика М.Ф. Решетнева» Филиал СибГУ в г. Лесосибирск Кафедра информационных и технических систем
Лесосибирск 2022
Содержание Задание 1 Расчет теоретических циклов поршневых ДВСИсходные данные:Цикл Тринклера, ε = 14 ;λ =1,7 ; ρ = 1,3 ; t1 = 0 °С; N = 70 кВт; сν = 0,71 кДж/(кг∙К); ср = 1,005 кДж/(кг∙К) Расчет параметров в характерных точках цикла и построение диаграммы в координатах Р–νР1 = 1∙105 Па (задано по условию) Т1 = 273 + t1 = 273 + 0 = 273 К Rμ = 8314 Дж/(кмоль∙К) μ = 28,9 кг/кмоль (молекулярная масса воздуха) R = = = 287,7 Дж/(кг∙К) ν1 = = = 0,785 м3/кг u1 = сνТ1 = 0,71∙273 = 193,8 кДж/кг h1 = срТ1 = 1,005∙273 = 274,4 кДж/кг Для нахождения параметров точки 2 цикла используют соотношение между параметрами Р, ν, Т в адиабатном процессе 1-2: ν2 = = = 0,056 м3/кг k = = 1,4 Р2 = Р1∙εk = 1∙105∙141,4 = 40,2∙105 Па = 40,2 бар Т2 = = = 782 К u2 = сνТ2 = 0,71∙782 = 555,2 кДж/кг h2 = срТ2 = 1,005∙782 = 785,9 кДж/кг Для определения параметров точки 3 используют соотношение между параметрами в изохорном процессе 2-3: Р3 = Р2∙λ = 40,2∙105∙ 1,7 = 68,3∙105 Па = 68,3 бар Т3 = Т2∙λ = 782∙1,7 = 1329 К ν3 = ν2 = 0,056 м3/кг u3 = сνТ3 = 0,71∙1329 = 943,6 кДж/кг h3 = срТ3 = 1,005∙1329 = 1335,6 кДж/кг Для определения параметров точки 4 используют соотношение между параметрами в изобарном процессе 3-4: Р4 = Р3 = 68,3∙105 Па = 68,3 бар Т4 = Т3∙ρ = 1329∙1,3 = 1728К ν4 = ν3∙ρ = 0,056∙1,3 = 0,073 м3/кг u4 = сνТ4 = 0,71∙1728 = 1226,9 кДж/кг h4 = срТ4 = 1,005∙1728 = 1736,6 кДж/кг Для определения параметров точки 5 используют соотношение между параметрами в адиабатном процессе 4-5 и изохорном процессе 5-1: ν5 = ν1 = 0,785 м3/кг Р5 = Р4 k= 68,3∙105 1,4 = 2,5∙105 Па = 2,5 бар Т5 = = = 682 К u5 = сνТ5 = 0,71∙682 = 484,2 кДж/кг h5 = срТ5 = 1,005∙682 = 685,4 кДж/кг Расчет промежуточных точек. Точка a на изоэнтропе 1-2: Примем ра = 10,16,1∙105 Па νа = ν1 = 0,785∙ = 0,149 м3/кг Точки b и c на изоэнтропе 4-5: Примем рb = 35,429,1105 Па νb = ν4 = 0,073∙ = 0,116 м3/кг Примем рс = 98,2∙105 Па νс = ν4 = 0,073∙ = = 0,056 м3/кг Результаты расчетов сводят в таблицу 1.1. Таблица 1.1. Результаты расчетов основных термодинамических показателей в узловых точках
Таблица 1.2.
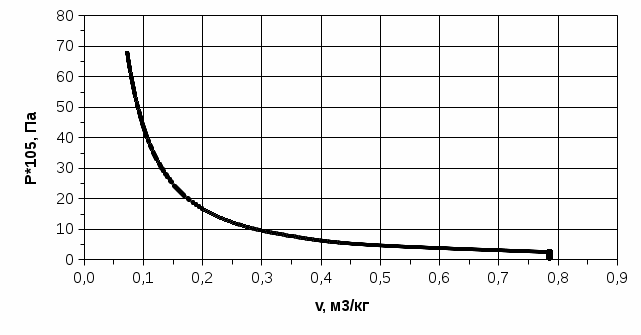 Рисунок 1.1. Цикл Тринклера в Р- ν координатах 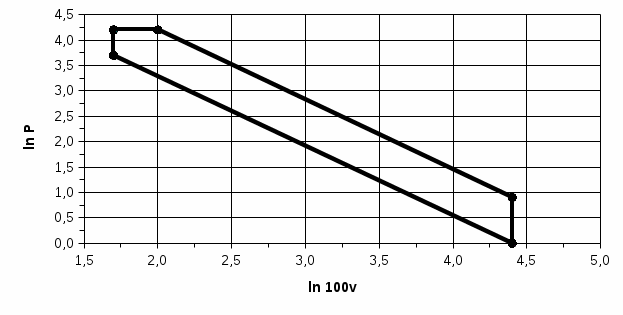 Рисунок 1.2. Цикл Тринклера в координатах ln Р-ln 100ν Расчет параметров в характерных точках цикла и построение диаграммы в координатах Т-sЗначение энтропии в точке 1 s1 = cpln - Rln = 1,005 ln - 287,7ln = 3,93 кДж/(кг∙К) Изменение энтропии в процессах: Δs1-2 = 0 (т.к. процесс изоэнтропный) Δs2-3 = сν ln = 0,71∙ln = 0,38 кДж/(кг∙К) Δs3-4 = ср ln = 1,005∙ln = 0,26 кДж/(кг∙К) Δs4-5 = 0 (т.к. процесс изоэнтропный) Δs5-1 = сν ln = 0,71∙ln = -0,64 кДж/(кг∙К) Расчет промежуточных точек d и e, задав для них значения температур, для построения изохоры 2-3: Тd = 900 К, Δs2-d = сν ln = 0,71∙ln = 0,1 кДж/(кг∙К) Те = 1100 К, Δs2-е = сν ln = 0,71∙ln = 0,24 кДж/(кг∙К) Расчет промежуточных точек f, q, и h, задав для них значения температур, для построения изохоры 5-1: Тf = 350 К, Δs1-f = сν ln = 0,71∙ln = 0,2 кДж/(кг∙К) Тq = 450 К, Δs1-f = сν ln = 0,71∙ln = 0,35 кДж/(кг∙К) Тh = 550 К, Δs1-f = сν ln = 0,71∙ln = 0,5 кДж/(кг∙К) Расчет промежуточных точек i и j, задав для них значения температур, для построения изобары 3-4: Тi = 1500 К, Δs3-i = ср ln = 1,005∙ln = 0,12 кДж/(кг∙К) Тj = 1600 К, Δs3-j = ср ln = 1,005∙ln = 0,18 кДж/(кг∙К) 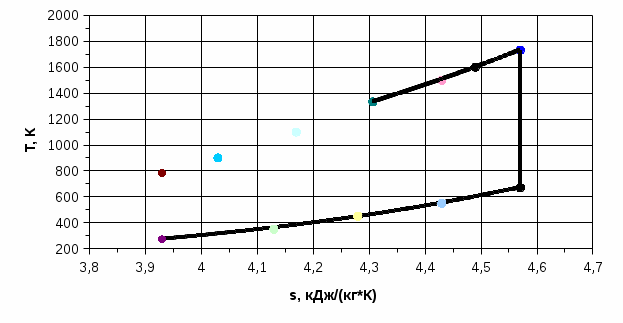 Рисунок 1.3. Цикл Тринклера в координатах Т-s Приращение энтропии в изобарном и изохорном процессах в диапазоне температур от Т1 до Т2: ΔsP1-2 = сp ln = 1,005∙ln = 1,06 кДж/(кг∙К) Δsν1-2 = сν ln = 0,71∙ln = 0,75 кДж/(кг∙К) Приближенный расчет изменения внутренней энергии и энтальпии в изоэнтропном процессе 1-2: Δu1-2 = Δsν1-2 = 0,75∙ = 396 кДж/кг Δh1-2 = ΔsР1-2 = 1,06∙ = 559 кДж/кг Из первого закона термодинамики следует, что q =Δu +l. По условию адиабатного процесса q = 0. Следовательно l = - Δu = -396 кДж/кг Т2 = 782 К, Т3 = 1329 К; ΔsP2-3 = сp ln = 1,005∙ln = 0,53 кДж/(кг∙К) Δsν2-3 = сν ln = 0,71∙ln = 0,38 кДж/(кг∙К) Приближенный расчет изменения внутренней энергии и энтальпии в изохорном процессе 2-3: Δu2-3 = Δsν2-3 = 0,38∙ = 401 кДж/кг Δh2-3 = ΔsР2-3 = 0,53∙ = 559 кДж/кг q2-3 = Δu2-3 = 401 кДж/кг Т3 = 1329 К, Т4 = 1728 К. ΔsP3-4 = сp ln = 1,005∙ln = 0,26 кДж/(кг∙К) Δsν3-4 = сν ln = 0,71∙ln = 0,19 кДж/(кг∙К) Приближенный расчет изменения внутренней энергии и энтальпии в изобарном процессе 3-4: Δu3-4 = Δsν3-4 = 0,19∙ = 290 кДж/кг Δh3-4 = ΔsР3-4 = 0,26∙ = 397 кДж/кг q3-4 = ср(Т4 – Т3) = 1,005(1728 - 1329) = 1051,2 кДж/кг l3-4 = P3∙(V4 – V3) = 68,3∙105(0,073 - 0,056) = 116,11 кДж/кг Т4 = 1728 К, Т5 = 682 К. ΔsP4-5 = сp ln = 1,005∙ln = -0,96 кДж/(кг∙К) Δsν4-5 = сν ln = 0,71∙ln = -0,67 кДж/(кг∙К) Приближенный расчет изменения внутренней энергии и энтальпии в изоэнтропном процессе 4-5: Δu4-5 = Δsν4-5 = -0,67∙ = -807 кДж/кг Δh4-5 = ΔsР4-5 = -0,96∙ = -1157 кДж/кг l4-5 = -Δu4-5 = 807 кДж/кг Т5 = 682 К, Т1 = 273 К. ΔsP5-1 = сp ln = 1,005∙ln = -0,9 кДж/(кг∙К) Δsν5-1 = сν ln = 0,71∙ln = -0,64 кДж/(кг∙К) Приближенный расчет изменения внутренней энергии и энтальпии в изохорном процессе 5-1: Δu5-1 = Δsν5-1 = -0,64∙ = -306 кДж/кг Δh5-1 = ΔsР5-1 = -0,9∙ = -430 кДж/кг q5-1 = Δu5-1 = -306 кДж/кг Результаты приближенных расчетов сводим в таблицу 1.3. Таблица 1.3. Результаты приближенных расчетов.
Количество тепла подводимого к телу в процессе 2-3: q2,3 = сν(Т3 – Т2) = 0,71(1329 – 782) = 388 кДж/кг Количество тепла подводимого к телу в процессе 3-4: q3,4 = ср(Т4 – Т3) = 1,005(1728 – 1329) = 401 кДж/кг Общее количество теплоты подведенное в цикле: q1 = q2,3 + q3,4 = 388+401 = 789 кДж/кг Количество тепла отводимого от тела в процессе 5-1: q2 = сν(Т5 – Т1) = 0,71(682 – 273) = 290 кДж/кг Работа, совершаемая в цикле: l0 = q1 - q2 = 789 - 290 = 499 кДж/кг Термический КПД цикла: ηt = = = 0,632 Количества воздуха, совершающего работа в цилиндрах двигателя при мощности N = 70 кВт. М = = = 0,140 кг/с Количества тепла, сообщаемого рабочему телу за 1 с при мощности 70 кВт: Q1 = Mq1 = 0,14∙789 = 110 кДж/с = 110 кВт Количества тепла, отводимого от рабочего тела за 1 с при мощности 70 кВт: Q2 = Mq2 = 0,14∙290 = 41 кДж/с = 41 кВт Термический КПД цикла так же можно рассчитать по формуле: ηt = 1 – ∙ = 1 - ∙ = 0,642 Полученная величина ηt незначительно отличается от полученной ранее. Задание 2 Расчет поршневого компрессораИсходные данные:P1 = 0,1 МПа; t1 = 27 ºC; Δt = 195 ºC; Рк = 6 МПа; n = 1,32 ; G = 0,4 кг/с Выведем формулу для определения числа ступеней при допустимом Δt. Конечная температура сжатия в цилиндре: Т2 = Т1х (n-1)/n (1) Степень повышения давления: х = = 1/z (2) где z – число ступеней. Подставим формулу (2) в (1) получим: Т2 = Т1(n-1)/(zn) (3) Величина повышения температуры: Δt = Т2 – Т1 = Т1(n-1)/(zn)- Т1 = Т1, (4) откуда число ступеней: z = ∙ (5) Температура в начале сжатия: Т1 = t1 + 273 = 27 + 273 = 300К z = ∙ = 1,98 Принимаем число ступеней z = 2 Степень повышения давления: х = = 7,746 Расчет ступеней компрессора. Ступень 1. Т1 = 300 К Т2 = Т1х(n-1)/n = 300∙7,746(1,32-1)/1,32 = 493 К Р2 = P1∙x = 0,1∙7,746 = 0,775 МПа Т.к. после сжатия (точка 2) происходит изобарное охлаждение(точка 3) до T1, то: Р3 = P2 = 0,775МПа T3 = Т1 = 300 К Величины объемов в этих точках: v1 = (6) где R = 287 Дж/(кг∙К) – газовая постоянная воздуха. v1 = = 0,861 м3/кг v2 = = 0,183 м3/кг v3 = = 0,111 м3/кг Ступень 2. Т3 = 300 К Т4 = Т3х(n-1)/n = 300∙7,746(1,32-1)/1,32 = 493 К Р4 = P3∙x = 0,775∙7,746 = 6,003 МПа Т.к. после сжатия (точка 4) происходит изобарное охлаждение(точка 5) до T3, то: Р5 = P4 = 6,003МПа T5 = Т3 = 300 К Величины объемов в этих точках: v4 = = 0,024 м3/кг v5 = = 0,014 м3/кг Таблица 2.1. Значение основных параметров в узловых точках.
Значение энтропии в точке1: s1 = cpln - Rln (7) где Тн = 273 К, Рн = 101375 Па, ср = 1005 Дж/(кг∙К) s1 = 1005ln - 287ln = 0,0987 кДж/(кг∙К) Изменение энтропии в процессе 1-2: Δs1-2 = cpln - Rln = 1005ln - 287ln = -0,0889 кДж/(кг∙К) Изменение энтропии в процессе 2-3: Δs2-3 = cpln = 1005∙ln = -0,4988 кДж/(кг∙К) Изменение энтропии в процессе 3-4: Δs3-4 = cpln - Rln = 1005ln - 287ln = -0,0889 кДж/(кг∙К) Изменение энтропии в процессе 4-5: Δs4-5 = cpln = 1005∙ln = -0,4988 кДж/(кг∙К) Строим диаграммы в координатах Р-v, и Т-s. 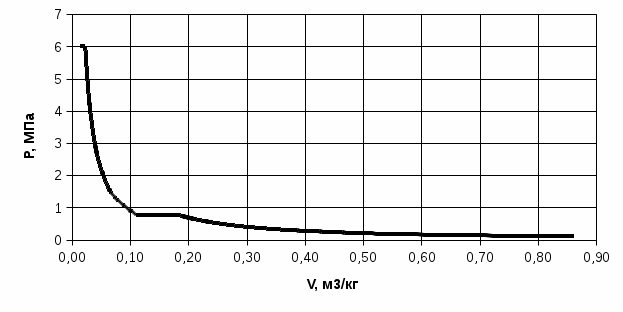 ∙Рисунок 2.1. Диаграмма работы идеального трехступенчатого компрессора в Р-v координатах. 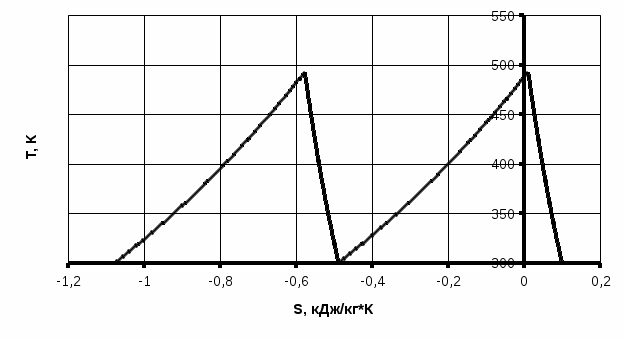 Рисунок 2.2. Диаграмма работы идеального трехступенчатого компрессора в Т-s координатах. Затраченная работа: l0 = z RT1(х(n-1)/n – 1) = 2∙∙287∙300(7,746(1,32-1)/1,32 -1)= 26,8 кДж/кг Необходимая мощность привода: N = Gl0 = 0,4∙26,8 = 10,7 кВт Теплота отведенная от стенок цилиндров компрессора: q1-2 = z∙сn(T2 – T1); cn = cv , k = cv = cp – R = 1005-287 = 718 Дж/(кг∙К), k = = 1,4 cn =718 = -179,50 Дж/(кг∙К) q1-2 = 2∙(-179,5)∙(493 – 300) = -69,3 кДж/кг Количество теплоты отведенное в ресиверах: q2-3 = zcp(Т2-Т1) = 2∙1,005(493 – 300) = 387,9 кДж/кг Задание 3 Расчет холодильного цикла Исходные данные t1 = -15 °C, t2 = 25 °C, Q = 130 кВт. По таблице свойств хладона-12 (табл. 7 приложения) на линии насыщения по t1 и t2 определяют: Р1 = 0,183 МПа; Р2 = 0,6508 МПа  = 3,9476 кДж/(кг∙К);  = 4,0836 кДж/(кг∙К) = 4,5648 кДж/(кг∙К);  = 4,5485 кДж/(кг∙К) = 385,98 кДж/кг  = 425,13 кДж/кг = 545,26 кДж/кг  = 562,73 кДж/кг = 0,000693 м3/кг  = 0,000764 м3/кг = 0,09125 м3/кг  = 0,02712 м3/кгРасчет h, s, x, и ν в точках 1-4: s2 = (сухой насыщенный пар хладона-12);s2 = 4,5485 кДж/(кг∙К); s1 = s2 = 4,5485 кДж/(кг∙К) (обратимый адиабатный процесс); x1 = 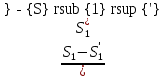 = = 0,9736;h1 = ∙x1 + (1 – x1) = 545,26∙0,9736 + (1 - 0,9736)∙385,98 = 541,1 кДж/кг;ν1 = ∙x1 + (1 – x1) = 0,09125∙0,9736 + (1 - 0,9736)∙0,000693 = 0,08886 м3/кг;h2 = (сухой насыщенный пар хладона-12 (х2 = 1));h2 = 562,73 кДж/кг; ν2 = (сухой насыщенный пар хладона-12 (х2 = 1));ν2 = 0,02712 м3/кг; s3 = (жидкость хладона в стадии насыщения (х3 = 0));s3 = 4,0836 кДж/(кг∙К); h3 = ;h3 = 425,13 кДж/кг; ν3 = ν3 = 0,000764 м3/кг h4 = h3 = 425,13 кДж/кг;  = = 38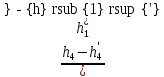5,98 кДж/кг;  = = 545,26 кДж/кг;x4 =  = = 0,2458; = = 3,9476 кДж/(кг∙К); = = 4,5648 кДж/(кг∙К);s4 = ∙х4 + (1-х4) = 4,5648∙0,2458 + (1-0,2458)∙3,9476 = 4,0993 кДж/(кг∙К); = = 0,000693 м3/кг; = = 0,09125 м3/кг;ν4 = ∙х4+(1-х4)∙ = 0,09125∙0,2458+(1+0,2458)∙0,000693 = 0,02295 м3/кг.Далее значение термодинамических параметров в узловых точках сводят в таблицу 3.1. Таблица 3.1. Значение термодинамических параметров в узловых точках
Холодильный коэффициент установки: ε = = = 5,36 Максимально возможный холодильный коэффициент εmax для заданных исходных условий соответствует значениям t1 и t2 случайно обратимому процессу адиабатного расширения 3-4: εmax = = = 6,45 Расход фреона: m = = = = 1,12 кг/с Мощность привода: N = m∙l = m(h2 – h1) = 1,12∙(562,73-541,1) = 24,2 кВт  Рисунок 3.1. Принципиальная схема парокомпрессорной холодильной установки 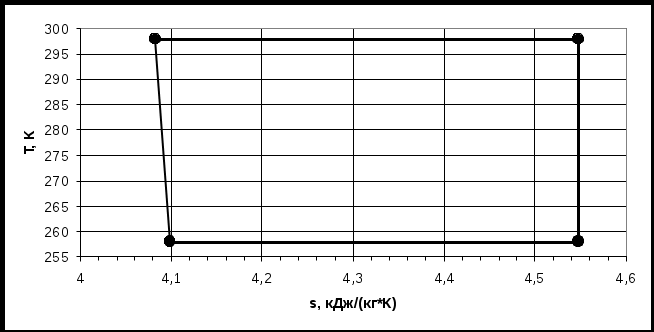 Рисунок 3.2. Цикл парокомпрессорной холодильной установки в Т-s координатах 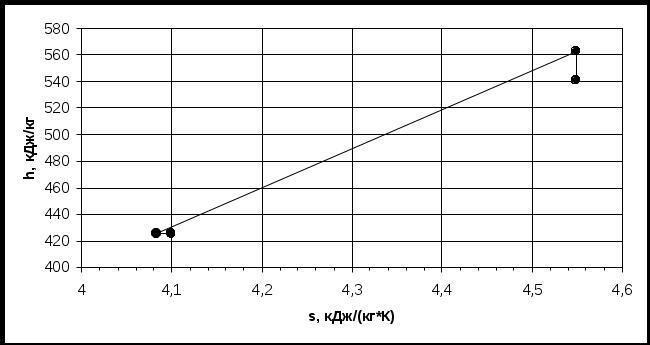  Рисунок 3.3. Цикл парокомпрессорной холодильной установки в h-s координатах Задание 4 Расчет теплопередачи через стенку горизонтально расположенной цилиндрической трубы По горизонтально расположенной стальной трубе, внутренний и внешний диаметры которой соответственно равны d1 и d2, а коэффициент теплопроводности λст = 40 Вт/(м∙К), протекает вода со скоростью wводы и средней температурой tводы. Снаружи труба охлаждается воздухом, температура которого tвозд = 20°С. Степень черноты наружной поверхности εтр. Требуется определить: 1) средний линейный коэффициент теплопередачи k от воздуха к воде; 2) удельный линейный тепловой поток при поперечном обдуве трубы воздухом со скоростью wвозд; 3) удельный линейный тепловой поток в случае wвозд= 0 м/с. Исходные данные: d1 = 0,04 м; wводы= 0,9 м/с; tводы = 90 °С; εтр = 0,8 ; d2 = 0,05 м; wвозд = 14 м/с; tвозд = 20°С; λст = 40 Вт/(м∙К). Решение: По табл. 15 приложения находим νводы, Рг и λводы при tводы = 90 °С: νюды = 0,326 ∙10-6 м2/с, Ргводы = 1,95 , λводы = 0,68 Вт/(м∙°С). По табл. 14 приложения находим νвозд, Рг и λвозд при tвозд = 20 °С: νвозд = 15,06∙10-6 м2/с, Ргвозд = 0,703, λвозд = 0,0259 Вт/(м∙°С) При движении жидкости в трубе критерий Рейнольдса: Re = wводыd1νюды Re = 0,9∙0,040,326∙10 6 = 110429 > 104, следовательно режим движения турбулентный. Критерий Нуссельта: Nu1 = 0,021∙Re0,8∙Pr0,43 Nu1 = 0,021∙1104290,8∙1,950,43 = 303,0 Коэффициент теплоотдачи на внутренней поверхности трубы: α1 = Nu1∙λводыd1 α1 = 303∙0,680,04 =5151,0 Вт/(м2∙К) При свободной конвекции около горизонтальной трубы (wвозд= 0 м/с): β = 1Твозд = 120+273 = 3,4∙10-3 К-1; Критерий Грасгофа: Gr = gβ(tводы - tвозд)d23ν2возд Gr = 9,8∙3,4∙10-3(90 - 20)0,05315,062∙10-12 = 1,29∙106 (Gr∙Prвозд) = 1,29∙106∙0,703 = 0,907∙106 Критерий Нуссельта в данном случае: Nu2 = 0,5(Gr∙Prвозд)0,25 Nu2 = 0,5∙(0,907∙106)0,25 = 15,43 Коэффициент теплоотдачи на наружной поверхности трубы при конвективном теплообмене: α2 = Nu2∙λвоздd2 α2к = 15,43∙0,02590,05 = 7,99 Вт/(м2∙К) Количество тепла, переданное трубой в окружающую среду путем излучения: qл = εтрС0 Тводы1004 - Твозд1004 qл = 0,8∙5,67 3631004 - 2931004 = 453,3 Вт/м2 Условный коэффициент теплоотдачи при лучистом теплообмене: α2л = qлtводы - tвозд α2л = 453,390 - 20 = 6,48 Вт/(м2∙К) Суммарный коэффициент теплоотдачи: 0,2231 α2 = α2к + α2л α2 = 7,99 + 6,48 = 14,47 Вт/(м2∙К) Линейный коэффициент теплопередачи при свободной конвекции: kс.к. = 11d1α1 + 12λст ∙ lnd2d1+ 1d2α2 kс.к. = 110,04∙5151 + 12∙40 ∙ ln0,05 0,04+ 10,05∙14,47 = 0,720 Вт/(м∙К) Удельный линейный тепловой поток: ql = π kс.к(tводы - tвозд) qlс.к. = 3,14∙0,72(90 - 20) = 158,26 Вт/м Температура внутренней поверхности: t1 с.к. = tводы - qlс.кα1d1π t1с.к. = 90 - 158,265151∙0,04∙3,14 = 89,76 ºС Температура наружной поверхности: t2с.к. = t1с.к. - 12λст∙lnd2d1 t2с.к. = 89,76 - 158,262∙3,14∙40∙ln0,050,04 = 89,62ºС При вынужденной конвекции (wвозд = 14 м/с): Критерий Рейнольдса: Re = wвоздd2νвозд Re = 14∙0,0515,06∙10-6 = 46,48∙103 При 103< Re<2∙105, критерий Нуссельта равен: Nu3 = 0,25Re0,6∙Pr0,38 Nu3 = 0,25∙(46,48∙103)0,6∙0,7030,38 = 138,08 Коэффициент теплоотдачи на наружной поверхности трубы при конвективном теплообмене: α3 = Nu3λвоздd2 α3к = 138,08∙0,02590,05 = 71,53 Вт/(м∙К) Суммарный коэффициент теплоотдачи: α3 = α3к + α2л α3 = 71,53 + 6,48 =78,01 Вт/(м∙К) Линейный коэффициент теплопередачи: kв.к. = 11d1α1 + 12λст ∙ lnd2d1+ 1d2α3 kв.к. = 110,04∙5151 + 12∙40 ∙ ln0,05 0,04+ 10,05∙78,01 = 3,788 Вт/(м∙К) Удельный линейный тепловой поток: ql = π kв.к(tводы - tвозд) qlв.к. = 3,14∙3,788(90 - 20) = 832,60 Вт/м Температура внутренней поверхности: t1в.к. = tводы - qlв.кα1d1π t1в.к. = 90 - 832,65151∙0,04∙3,14 = 88,71 ºС Температура наружной поверхности: t2в.к. = t1в.к. - 12πλст∙lnd2d1 t2в.к. = 88,71 - 832,62∙3,14∙40∙ln0,050,04 = 87,97ºС Вывод. С увеличением скорости газа при поперечном омывании им цилиндрической трубы возрастает коэффициент теплопередачи и, соответственно, удельный линейный тепловой поток k. Заключение В данной расчетно-графической работе решены четыре задачи. В первой задаче рассчитан термодинамический цикл Тринклера. Это цикл со смешанным подводом теплоты, по которому работают современные бескомпрессорные дизели. Во второй задаче рассчитан трёхступенчатый поршневой компрессор (без учета трения и вредного пространства). Из расчётов следует, что по мере повышения давления нагнетания снижается производительность компрессора, поэтому для получения высоких давлений применяются многоступенчатые компрессоры, в которых после каждой ступени газ поступает в промежуточный холодильник, где охлаждается при постоянном давлении до исходной температуры. В третьей задаче проведён расчёт парокомпрессионной холодильной установки. Из компрессора фреон поступает в конденсатор, где при постоянном давлении обращается в жидкость, после чего изоэнтальпийно расширяется в дросселе до начальной температуры. Определили холодильный коэффициент установки, массовый расход фреона, а также теоретическую мощность привода компрессора. В четвёртой задаче проведён расчёт теплопередачи через стенку горизонтально расположенной цилиндрической трубы. Расчёт показал, что с увеличением скорости газа при поперечном омывании цилиндрической трубы возрастает коэффициент теплопередачи и соответственно удельный тепловой поток. Список используемых источников 1. Теплотехника: учеб. для вузов [Текст] / В. Н. Луканин, [и др.]; под ред. В. Н. Луканина. – М.: Высшая школа, 1999. – 671 с. 2. Крутов, В. И. Теплотехника: учебник для вузов [Текст] / В. И. Крутов. М.: Машиностроение, 1986. – 432 с. 3. Кирилин, В. А. Техническая термодинамика [Текст] / В. А. Кирилин, В. В. Сычев, А. Е. Шейдлин. – М.: Энергия, 1974. – 447 с. 4. Техническая термодинамика [Текст] / В. И. Крутов, [и др.]. – М.: Высшая школа, 1991. – 384 с. 5. Богданов, С. Н. Холодильная техника. Свойства веществ [Текст] / С. Н. Богданов, О. П. Иванов, А. В. Куприянова: справочник. изд. 3-е, перераб. и доп. – М.: Агропромиздат., 1985. – 208 с. 6. Рабинович, О. М. Сборник задач по технической термодинамике. [Текст] / О. М. Рабинович. – М.: Машиностроение, 1973. – 344 с. 7. Андрианова, Т. Н. Сборник задач по термодинамике [Текст] / Т. Н. Андрианова, Б. В. Дзампов, В. Н. Зубарев, С. А. Ремизов: учеб. пособие для вузов.3-е изд., перераб. и доп. – М.:Энергоиздат., 1981. – 240с. 8. Нащокин, В. В. Техническая термодинамика и теплопередача [Текст] / В. В. Нащокин: учеб. пособие для вузов. 3-е изд., испр. и доп. – М.: Высшая школа, 1980. – 469 с. 9. Кушнырев, В. И. Техническая термодинамика и теплопередача. [Текст] / В. И. Кушнырев, В. И. Лебедев, В. А. Павленко. – М.: Строй издат., 1986. – 464 с. 10. Исаченко, В. П. Теплопередача [Текст] / В. П. Исаченко, В. А. Осипова, А. С. Сукомел. – М.: Энергоиздат, 1981. – 416 с. 11. Карташов, Э. М. Аналитические методы в теории теплопроводности твердых тел [Текст] / Э. М. Карташов.– М.: Высшая школа, 2001. – 539 с. 12. Краснощеков, Е. А. Задачник по теплопередаче [Текст] / Е. А. Краснощеков, А. С. Сукомел. – М.: Энергия, 1980. – 287 с. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||