Машины опорных векторов Support vector machines (svm) 1 Информация о методе
 Скачать 111 Kb. Скачать 111 Kb.
|
|
Машины опорных векторов - Support vector machines (SVM) 1 Информация о методе Support vector machines (SVM) Машины опорных векторов - набор методов обучения с учителем (supervised learning methods) используемый для классификации данных, регрессионного анализа и поиска аномальных значений (classification, regression and outliers detection). Преимущества SVM: Эффективен на пространствах большой размерности, то есть тогда когда объекты имеют много параметров остается эффективным в случае когда количество измерений больше количества обучающих примеров использует подмножество тренировочных данных в функции выработки решений (support vector), что обеспечивает эффективное использования памяти. Универсальность - могут использоваться разные ядерные функции (Kernel functions), включая определенные пользователем Может быть настроен для классификации в несбалансированом множестве Недостатки Если количество примеров намного меньше числа свойств трудно избежать переобучения Не поддерживает напрямую вероятностные оценки принадлежности классу, они рассчитываются с помощью довольно трудоемкой кроссвалидационной функции SVC (support vector classifier) получает на вход массив примеров X и массив меток классов y согласованного размера, обучается с помощью метода fit(X,y) и может использоваться для классификации неизвестных объектов. При этом в процессе обучения классификатор настраивается на то, чтобы различать объекты двух классов (true\false), или может быть обучен различать объекты нескольких классов. При этом SVC и NuSVC поддерживает подход “one-against-one”, а LinearSVC “one-vs-the-rest”. В последнем случае классификатор создает n классификаторов для n классов, а в первом случае n_class * (n_class - 1) / 2 классификаторов, которые затем должны быть объединены с помощью decision_function_shape метода. Настройка классификатора выполняется параметрами C (регуляризация) и gamma (параметр ядра, в случае не линейного ядра 'rbf'). Чем меньше С тем более сглаженным получается разделительная поверхность (то есть тем большей обобщающей способностью обладает классификатор - underfit). При больших С классификатор настраивается на стопроцентную классификацию обучающих примеров (overfitting), соответственно снижается способность обощения. Параметр gamma определяет как влияет отдельный обучающий пример. При больших gamma объекты других классов должны быть ближе в пространстве признаков чтобы оказать влияние. Выбор указаных параметров критичен для оптимальной работы SVC Постановка задачи SVC - метод обучения с учителем, обеспечивающий в том числе классификацию данных. Метод выполняет как линейное разделение обхектов, так и нелинйное за счет применения различных функций ядра Задача: Используя различные наборы данных оценить возможности классификации наборов данных с помощью SVC и визуализировать полученный результат. Данные Во первых, подключим необходимые компоненты и настроим цветовую палитру для отображения: %matplotlib notebook import numpy as np import matplotlib.pyplot as plt from sklearn.model_selection import train_test_split from sklearn.datasets import make_classification, make_blobs from matplotlib.colors import ListedColormap cmap_bold = ListedColormap(['#FFFF00', '#00FF00', '#0000FF','#000000']) В качестве данных сгенерируем два набор данных. первый из которых хорошо разделяется линейными методами, второй разделить прямой не возможно. Каждый набор будет содержать объекты двух классов в количестве 100 штук, описываемые 2 параметрами: X_C2, X_D2 и метки объектов (массивы чисел 0 и 1) y_C2, y_D2. Набор X_C2, y_D2 используется для обучения и классификации SVC с линейным ядром. Наборы данных показаны на рисунке 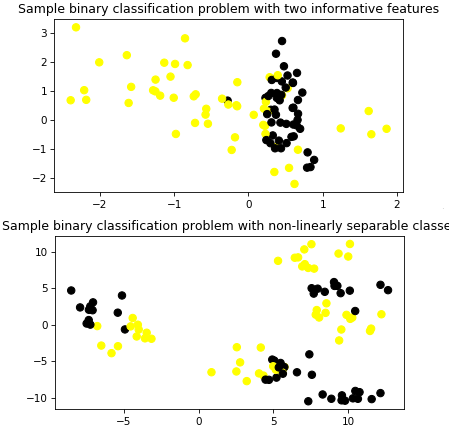 Метод решения Подключим необходимые библиотеки from sklearn.svm import SVC from sklearn.metrics import confusion_matrix, classification_report from adspy_shared_utilities import plot_class_regions_for_classifier_subplot Набор разделяется на обучающий и тестовый используя train_test_split(): X_train, X_test, y_train, y_test = train_test_split(X_C2, y_C2, random_state = 0) Классификатор обучается с предустановленным параметром C this_C = 5.0 clf = SVC(kernel = 'linear', C=this_C).fit(X_train, y_train) Вывод программы 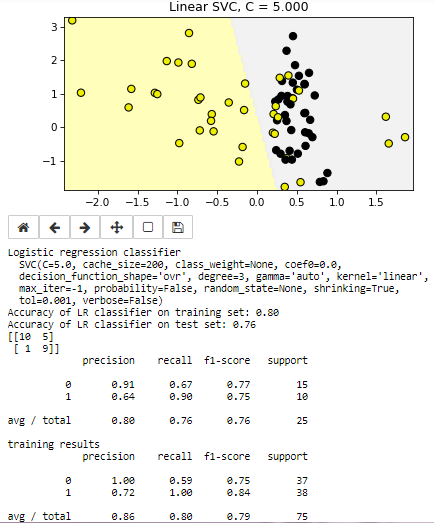 Программа показывает границу между классами, выводит параметры классификатора и параметры точности на тестовом и обчающем множествах Листинг программы MLF_SVM001 %matplotlib notebook import numpy as np import pandas as pd import matplotlib.pyplot as plt from sklearn.model_selection import train_test_split from sklearn.datasets import make_classification, make_blobs from matplotlib.colors import ListedColormap #from sklearn.datasets import load_breast_cancer #from adspy_shared_utilities import load_crime_dataset cmap_bold = ListedColormap(['#FFFF00', '#00FF00', '#0000FF','#000000']) ##### synthetic datasets ######################### # synthetic dataset for classification (binary) plt.figure() plt.title('Sample binary classification problem with two informative features') X_C2, y_C2 = make_classification(n_samples = 100, n_features=2, n_redundant=0, n_informative=2, n_clusters_per_class=1, flip_y = 0.1, class_sep = 0.5, random_state=0) plt.scatter(X_C2[:, 0], X_C2[:, 1], c=y_C2, marker= 'o', s=50, cmap=cmap_bold) plt.show() # more difficult synthetic dataset for classification (binary) # with classes that are not linearly separable X_D2, y_D2 = make_blobs(n_samples = 100, n_features = 2, centers = 8, cluster_std = 1.3, random_state = 4) y_D2 = y_D2 % 2 plt.figure() plt.title('Sample binary classification problem with non-linearly separable classes') plt.scatter(X_D2[:,0], X_D2[:,1], c=y_D2, marker= 'o', s=50, cmap=cmap_bold) plt.show() ############ Using SVM ##################### # from sklearn.svm import SVC from sklearn.metrics import confusion_matrix, classification_report from adspy_shared_utilities import plot_class_regions_for_classifier_subplot X_train, X_test, y_train, y_test = train_test_split(X_C2, y_C2, random_state = 0) fig, subaxes = plt.subplots(1, 1, figsize=(7, 5)) this_C = 5.0 clf = SVC(kernel = 'linear', C=this_C).fit(X_train, y_train) title = 'Linear SVC, C = {:.3f}'.format(this_C) plot_class_regions_for_classifier_subplot(clf, X_train, y_train, None, None, title, subaxes) predictions = clf.predict(X_test) print('Logistic regression classifier \n ', clf) print('Accuracy of LR classifier on training set: {:.2f}' .format(clf.score(X_train, y_train))) print('Accuracy of LR classifier on test set: {:.2f}' .format(clf.score(X_test, y_test))) matrix = confusion_matrix(y_test, predictions)#,labels) print(matrix) print(classification_report(y_test, predictions)) print('training results') predictions = clf.predict(X_train ) print(classification_report(y_train, predictions)) Задача 0 2. Используя сгенерированный набор данных X_D2, y_D2 оцените параметры точности классификатора и визуализируйте получившийся результат. По существу вам необходимо сделать минимальные изменения в вышеприведенной программе, заменив лишь анализируемый набор данным. Задача 1*3 Используя сгенерированный набор данных X_D2, y_D2, SVM c нелинейным ядром найдите оптимальное сочетание параметров С и gamma, обеспечивающих лучшие показательи точности классификации. Поиск С и gamma можно провести вручную, а можно воспользоваться операторами цикла. 1 https://scikit-learn.org/stable/modules/svm.html#scores-probabilities 2Решение MLF_SVM001_t0 3 Решение MLF_SVM001_t1 |
