мат. моделирование. РГР математическое моделирование Тянутов И. Е.. Математическое моделирование электрических систем и элементов
 Скачать 162.01 Kb. Скачать 162.01 Kb.
|
|
ФГБОУ ВО Уфимский государственный авиационный технический университет Кафедра электромеханики Расчетно-графическая работа по дисциплине «Математическое моделирование электрических систем и элементов» Выполнил: Группа ЭЭз-302 Тянутов И. Е. Проверил: К.т.н.,доцент ГусаковД.В. Уфа 2021 Цель работы: Научиться составлять математическую модель процесса, применяя законы электротехники, схемы замещения элементов энергосистемы и рассчитывать их параметры. Теоретическая часть Математические модели элементов ЭЭС. Линия электропередач. Физическая сущность большинства элементов в ЭЭС позволяет считать их, без особой погрешности, элементами с сосредоточенными параметрами, однако для линий электропередач (ЛЭП), особенно длинной свыше 50 км сверхвысокого и ультравысокого класса напряжения, учет распределенности их параметров во многих случаях становится необходим. При этом приближенный учет активных поперечных проводимостей ЛЭП является допустимым для точности воспроизведения реального спектра трехфазных процессов, а функциональное управление этой проводимостью позволяет учесть процесс коронирования ЛЭП. Кроме того, хотя распределенность параметров в ЛЭП неоднородна и ЛЭП в строгом представлении являются несимметричными, повсеместно используемое транспонирование ЛЭП симметрирует их. Таким образом, ЛЭП считаются симметричными и описываются известной, апробированной системой уравнений Исходные данные: P=1000 ; U=220 ; p=2 ; m=25 ; R =100 ; Ку = 30 ; X = 3 ; 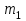 = 3 ; = 3 ; 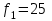 Используем заданные формулы . После чего были автоматически вычислены необходимые параметры. 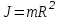 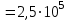 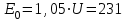 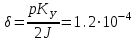 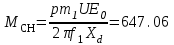  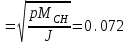 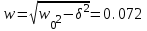 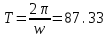 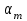 = 1 = 1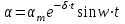 При изменении массы, радиуса ,коэффициента синхронизирующего моментаи коэффициента успокоительного момента при уменьшении заданных параметров получаются результаты. P=1000 ; U=220 ; p=2 ; m=12.5 ; R = 50 ; Ку = 15 ; X = 3 ; 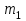 = 3 ; = 3 ; 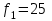 Используем заданные формулы . После чего были автоматически вычислены необходимые параметры. 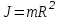 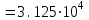 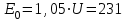 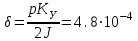 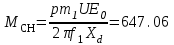 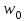 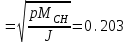 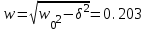 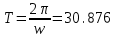 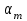 = 1 = 1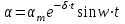 При изменении массы, радиуса ,коэффициента синхронизирующего моментаи коэффициента успокоительного момента при увеличении заданных параметров получаются результаты. P=1000 ; U=220 ; p=2 ; m=50 ; R =150 ; Ку =60 ; X = 3 ; 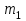 = 3 ; = 3 ; 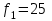 Используем заданные формулы . После чего были автоматически вычислены необходимые параметры. 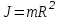 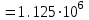 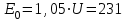 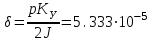 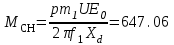 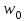 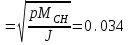  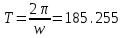 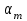 = 1 = 1 Графики для базисного значения , уменьшенного базисного значения и увеличенного базисного значений: 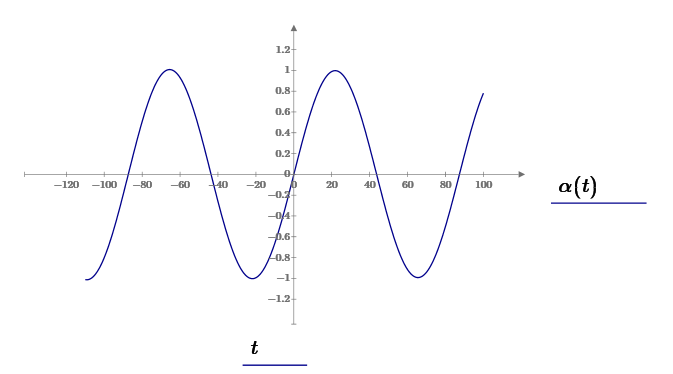 Рисунок 1-График для базисных значений 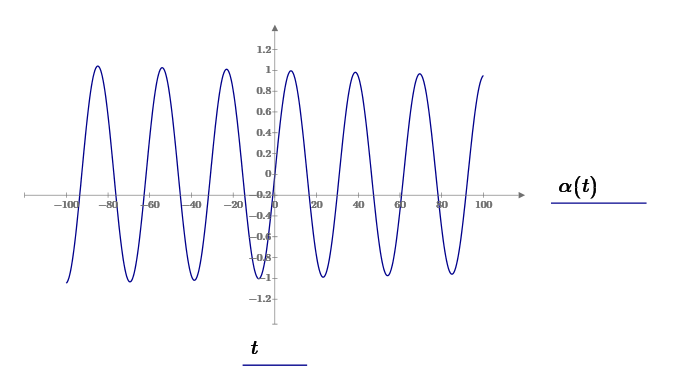 Рисунок 2-График для уменьшенного значения базисных значени 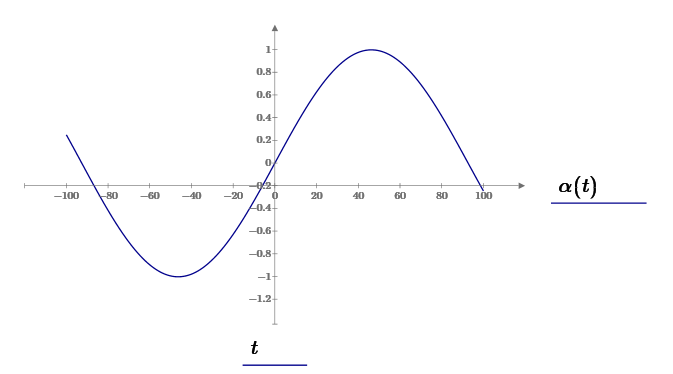 Рисунок3-График для увеличенного значения базисных значений Вывод: В ходе выполнения расчетно-графической работы были получены следующие умения : составлять математическую модель процесса, применяя законы электротехники, составлять схемы замещения элементов энергосистемы и рассчитать их параметры . Контрольные вопросыПри увеличении массы ротора частота затухания колебаний уменьшается, а скорость затухания колебаний увеличивается и на оборот, при уменьшении массы частота увеличивается, а скорость затухания уменьшается. При увеличении успокоительного момента - частота затухания увеличивается, а скорость затухания уменьшается; при уменьшении - частота уменьшается, а скорость затухания увеличивается При увеличении радиуса ротора частота затухания колебаний уменьшается, а скорость затухания колебаний увеличивается, а при уменьшении радиуса частота увеличивается, а скорость затухания уменьшается. При колебании ротора синхронного генератора внешний момент уравновешивают: электромагнитный момент, инерционный момент, синхронизирующий момент, успокоительный момент. |
