Математика и криминалистика Решение геометрических задач
 Скачать 3.2 Mb. Скачать 3.2 Mb.
|
|
Исследовательская работа на тему: «Математика и криминалистика Решение геометрических задач» Работу выполнили: Суворовцы Платов А.А Ветютнев Д.Д Руководитель: учитель математики Тасимова А.Д. Содержание: Введение Актуальность темы. Цель работы. Значение прикладных задач в криминалистике. Теоретическая часть. Практическая часть. Список использованной литературы. Приложение. Введение Криминалистика- наука, изучающая закономерности возникновения информации о преступлении, собирания , исследования, оценки и использования доказательств, исследующая механизм преступных деяний , особенности деятельности по раскрытию ,расследованию и предупреждению всех видов преступлений и разрабатывающая на этой основе средства и методы данной деятельности. Актуальность темы. В современном мире работа криминалиста является одной из самых важных. Каждый день он сталкивается с проблемами, которые он должен решать. Криминалист должен знать множество наук в совершенстве. Одна из наук является- математика. Зачем нужна эта точная наука эксперту криминалисту? Цель работы: 1. Расширение теоретической базы, аналитический обзор литературы. 2. Изучение геометрических методов в решении прикладных задач. 3. Развитие умений и навыков исследовательской работы и прикладное применение знаний в создании проекта. Значение прикладных задач в криминалистике. Решение прикладных задач имеет огромное значение в криминалистике и судебной экспертизе. Наибольшее применение в криминалистике, особенно в криминалистической технике, изучающей технические средства и методы работы с вещественными доказательствами, нашли геометрические методы. Благодаря их применению удается точно зафиксировать материальные следы преступлений и получить о них количественную информацию. Объективная фиксация размеров предметов, имеющих доказательное значение, способствует их индивидуализации. Наличие в уголовном деле точных данных о размерах определенных объектов и их частей, а также о расстояниях между предметами обстановки места происшествия дает возможность успешно анализировать вещественные доказательства с целью выяснения их роли в процессе подготовки к преступлению, при его раскрытии и сокрытии следов.(Рис 1, а,б) 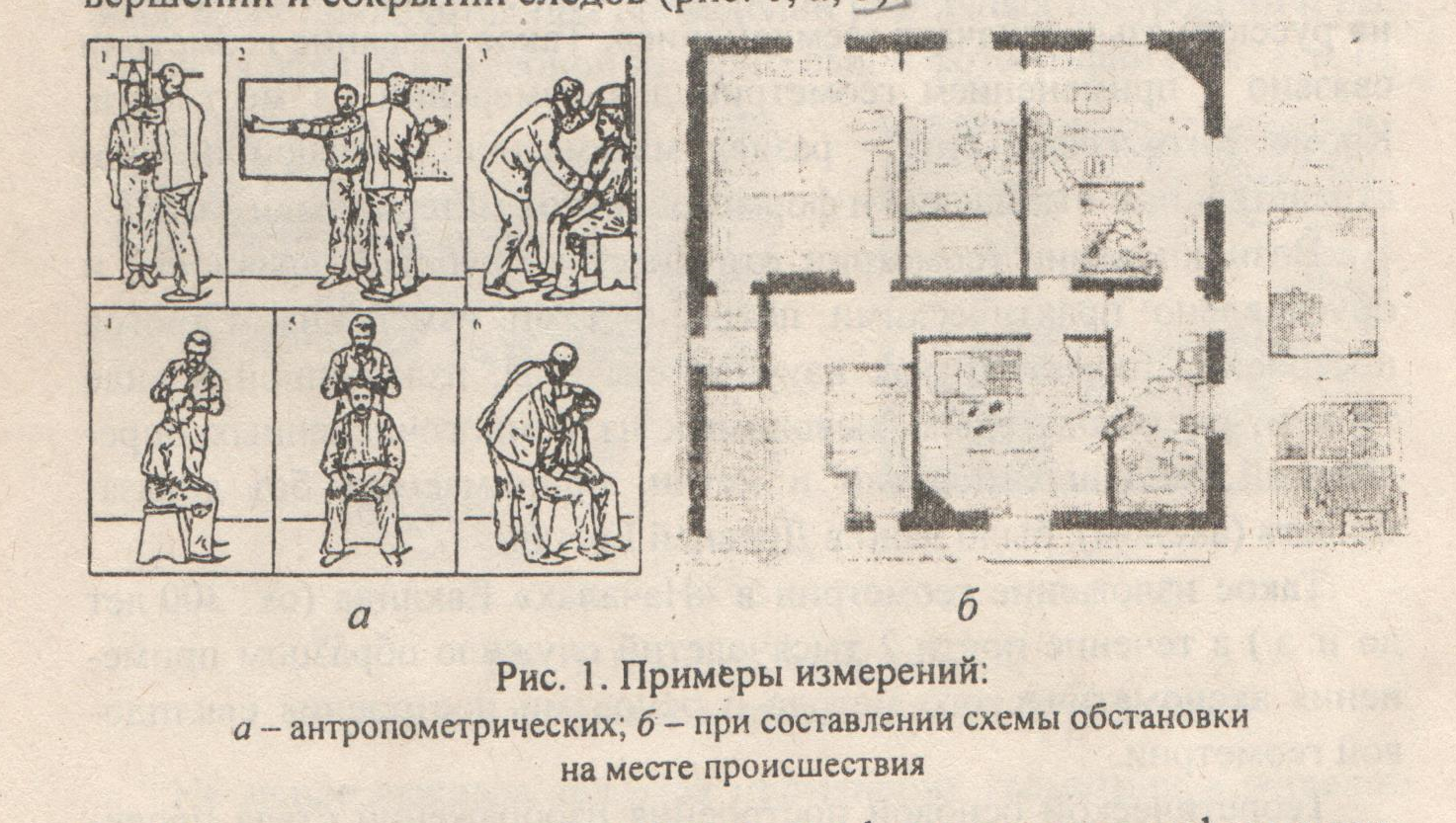 Методы геометрии применимы для формализации информации, полученной при изучении объектов криминалистических исследований – следов рук, ног, зубов человека, обуви, транспортных средств, орудий взлома, огнестрельного оружия, следов его применения, рукописных инструментов.(Рис 2) 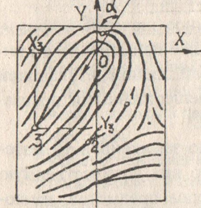 Рис 2 Методы проективной геометрии находят широкое применение в практике ряда идентификационных исследований. Довольно часто в решении практических задач используют положения из тригонометрии, которое представляет собой учение об отношениях между сторонами и углами треугольника. Многие важные для расследования вопросы выясняются с помощью тригонометрических функций. Последние применяются, например, при расчетах, производимых для определения точного места нахождения стрелявшего, в судебной баллистике, и с целью установления широты клинка холодного оружия по величине разреза – в трасологии. В криминалистике применяются измерительные геометрические методы и методы аналитической геометрии, представляющие собой комбинацию из элементарной алгебры и геометрии, методы проективной геометрии. Обращаться к геометрическим методам при решении прикладных задач приходится при проведении различных построений и расчетов, особенно в судебной измерительной фотографии.(Рис. 3 а,б)  Не менее важным является применение геометрии в решении задач кодирования и распознавания графической информации. Так , например , кодируется любая графическая информация о различныхобъектах криминалистических экспертиз при вводе её в компьютер ( почерк, следы и отпечатки рук). На основе методов кодирования созданы специальные алгоритмы для исследования и идентификации различных по сложности и располагающихся в разных ракурсах объектов и следов. Данные алгоритмы реализованы в виде компьютерных автоматизированных информационно-поисковых систем различных следов. Если нужно закодировать какой-нибудь графический объект, например, букву «П», её изображение помещают в первую четверть прямоугольной системы координат и условно делят на элементарные части (точки или отрезки). Координаты этих элементов и служат тождественной кодовой информацией о конфигурации данного письменного знака (объекта).( Рис 4) 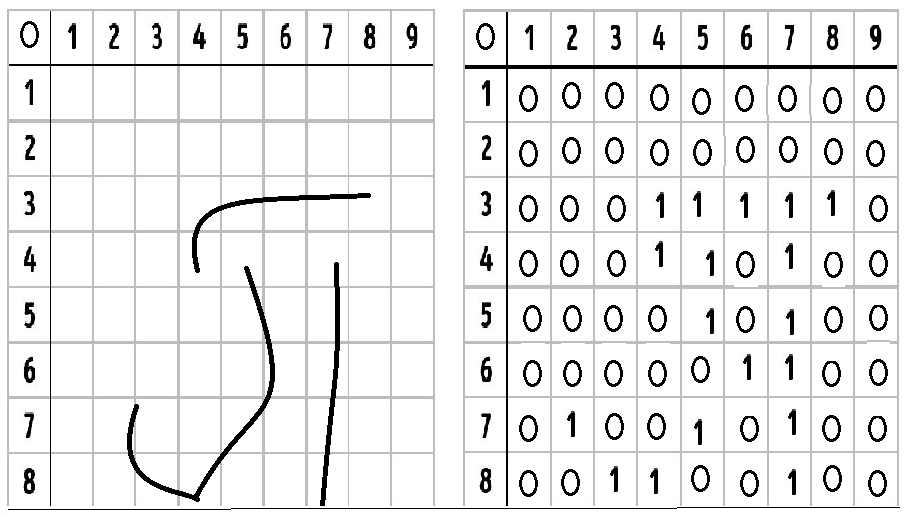 Рис 4 Теоретическая часть Трасология- раздел криминалистики , в котором изучаются теоретические основы следования, закономерности возникновения следов ,отражающих механизм преступления; разрабатываются рекомендации по применению методов и средств обнаружения следов, их фиксации, изъятия и анализа с целью установления обстоятельств , имеющих существенное значение для раскрытия, расследования и предупреждения преступления Геометрия –это наука о свойствах геометрических фигур. Слово «геометрия» - греческое (от гео. и.метрия), в переводе на русский язык означает «землемерие». Такое название геометрии связано с применением геометрии для измерений на местности. Кроме того, геометрия - раздел математики, изучающий пространственные отношения и формы объектов материального мира. При решении геометрических задач необходимо понять смысл понятий «равенство» . Под равенством понимается точное соответствие линейных и угловых величин сравниваемых геометрических фигур. 1. Решение прямоугольного треугольника по двум сторонам. Если даны две стороны прямоугольного треугольника, то третья сторона может быть вычислена по теореме Пифагора. (Теорема Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов). Определение острых углов производится по одной из формул, связывающих величины сторон и углов прямоугольного треугольника через функции синуса, косинуса и тангенса. (Синус угла -это отношение противолежащего катета к гипотенузе. Косинус угла-это отношение прилежащего катета к гипотенузе, Тангенсом угла называется отношение противолежащего катета к прилежащему катету). 2. Решение прямоугольного треугольника по одной стороне и острому углу. Если дан острый угол А , то величина угла С определяется по формуле С=90°-А, угол В прямой, равен 90°. Стороны можно найти по формулам. Приведенным выше, которые можно представить в следующем виде: a=b·sinA, a=b·cosC, a=c·tgA, c=b·sinC, c=b·cosA, c=a·tgC Практическая часть. Изучив необходимый теоретический материал, я обратился к эксперту криминалистики с просьбой самому решить некоторые задачи. Вот некоторые из них. 1) В доме № 45 по ул. Ленина , было совершенно ограбление (Рис 1) злоумышленники проникли в кв. №32 2-го этажа дома №46 . В кв №32 находилась веревка длиной 15 м благодаря которой злоумышленники проникли в квартиру Перед специалистом стоит задача: рассчитать длину AC для того чтобы понять в какой квартире находились злоумышленники. Известно, что расстояние между зданиями составляет 10 м, а расстояние от кв. №32 до земли составляет 10 м, расстояние между квартирами составляет 5 м. 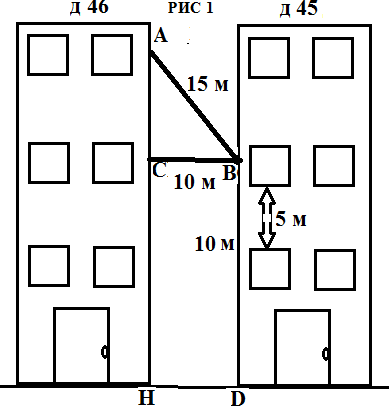 Решение: Веревка, протянутая с соседнего здания, образует прямой треугольник ABC Для нахождения стороны AC нужно применить теорему Пифагора: AC2=AB2-CB2 AC2= 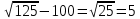 м мТеперь нам нужно найти расстояние AH для нахождения расстояния от квартиры до земли AH=10+5=15м Зная расстояние от земли до места, где была сброшена веревка, мы можем определить, на каком этаже находились злоумышленники: 15 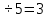 Этаж ЭтажОтвет: с 3-го этажа злоумышленники сбрасывали веревку. 2) Гражданину Nбыл нанесен смертельный удар в область груди. Специалисту необходимо предварительно установить вид холодного оружия, которым было совершено преступление. Для этого измеряют глубину раневого канала на теле, а также угол, под которым был нанесен удар. Необходимо определить ширину клинка холодного оружия по повреждению с целью установления вида холодного оружия. Длина повреждения (пореза) АВ=28 мм, угол, под которым клинок вошел в преграду α=30° (Рис 8) 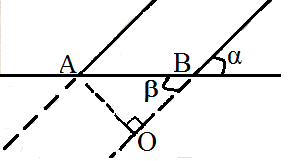 Угол α равен углу β ( вертикальные) . В треугольнике АВО известен угол = 30 и сторона АВ=28 мм. По определению синуса острого угла sinα=AO/AB, значит АО=АВ·sinα=28·0,5=14мм. Ответ: нож имеет длину 14мм Заключение. Методы геометрических задач находят широкое применение в практике. Благодаря их применению удаётся точно зафиксировать материальные следы преступлений и получить о них количественную информацию. Суть этого проекта – узнать, где используется геометрия в криминалистике и насколько важны прикладные задачи. перед нами стояли задачи: усвоение определенной системы знаний посредством моделирования и исследования реальных ситуаций. Закончив нашу исследовательскую деятельность, мы пришли к выводу, что подростки в возрасте 15-16 лет с большим интересом решают криминалистические задачи и рассуждают на тему судебной экспертизы. И стоявшие перед нами задачи с успехом были решены. И многие суворовцы стали более уверенны в выборе своей профессии. Список литературы: Ищенко Е.П., Любарский М.Г. В поисках истины.-М.: Юрид. лит., 1986.-128с. Использование математических методов в криминалистических экспертных исследованиях: уч. пос. \под ред. С. Я. Казанцева Криминалистика. Курс лекций/ М.И.Петров.- М.: Издательство «Экзамен»,2004.-288с. Перельман, Я. И. Занимательная геометрия. – Переизд. –Екатеринбург: Тезис, 1994. – 288 с. Перельман, Я. И. Занимательная алгебра. Занимательная геометрия. – М.: ООО «Издательство АСТ», 2005.- 474,(6) с. Селиванов, Н. А. Математические методы в собирании и исследовании доказательств. – М.: Юридическая литература,1974. – С. 9 – 21, 51 – 53, 59 – 63. АверьяноваТ.В., Белкин Р.С., Корухов Ю.Г., Россинская Е.Р. Криминалистика: Учебник для вузов/ Под ред.заслуженного деятеля науки РФ, проф.Р.С Белкина.- 2-е изд., перераб. И доп.-М.: Норма, 2005-992с. Россинская Е.Р. Криминалистика. Вопросы и ответы: Учеб.пособие для вузов.- М.:ЮНИТИ-ДАНА, 1999.-351с.-(Готовимся к экзамену) |
