|
|
MatLab Руководство для начинающих. Matlab сокращение от англ. Matrix Laboratory
5.2. Оператор цикла while
Язык программирования MatLab имеет два оператора цикла: while и for. С их помощью, например, выполняется программирование рекуррентных алгоритмов, подсчета суммы ряда, перебора элементов массива и многое другое.
В самом простом случае цикл в программе организуется с помощью оператора while, который имеет следующий синтаксис:
while <условие>
<операторы>
end
Здесь <условие> означает условное выражение подобное тому, которое применяется в операторе if, и цикл while работает до тех пор, пока это условие истинно.
Следует обратить внимание на то, что если условие будет ложным до начала выполнения цикла, то операторы, входящие в цикл, не будут выполнены ни разу.
Приведем пример работы цикла while для подсчета суммы ряда 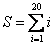 : :
S = 0; % начальное значение суммы
i=1; % счетчик суммы
while i <= 20 % цикл (работает пока i <= 20)
S=S+i; % подсчитывается сумма
i=i+1; % увеличивается счетчик на 1
end % конец цикла
disp(S); % отображение суммы 210 на экране
Теперь усложним задачу и будем подсчитывать сумму ряда 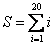 , пока , пока 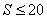 . Здесь в операторе цикла получается два условия: либо счетчик по i доходит до 20, либо значение суммы S превысит 20. Данную логику можно реализовать с помощью составного условного выражения в операторе цикла while: . Здесь в операторе цикла получается два условия: либо счетчик по i доходит до 20, либо значение суммы S превысит 20. Данную логику можно реализовать с помощью составного условного выражения в операторе цикла while:
S = 0; % начальное значение суммы
i=1; % счетчик суммы
while i <= 20 & S <= 20 % цикл (работает пока i<=10 и S<=20
S=S+i; % подсчитывается сумма
i=i+1; % увеличивается счетчик на 1
end % конец цикла
disp(S); % отображение суммы 21 на экране
Приведенный пример показывает возможность использования составных условий в цикле while. В общем случае в качестве условного выражения можно записывать такие же условия, что и в условном операторе if.
Работу любого оператора цикла, в том числе и while, можно принудительно завершить с помощью оператора break. Например, предыдущую программу можно переписать следующим образом с использованием оператора break:
S = 0; % начальное значение суммы
i=1; % счетчик суммы
while i <= 20 % цикл (работает пока i<=10
S=S+i; % подсчитывается сумма
i=i+1; % увеличивается счетчик на 1
if S > 20 % если S > 20,
break; % то цикл завершается
end
end % конец цикла
disp(S); % отображение суммы 21 на экране
В данном примере второе условие завершения цикла, когда S будет больше 20, записано в самом цикле и с помощью оператора break осуществляется выход из цикла на функцию disp(), стоящую сразу после цикла while.
Второй оператор управления выполнением цикла continue позволяет пропускать выполнение фрагмента программы, стоящий после него. Например, требуется подсчитать сумму элементов массива
a = [1 2 3 4 5 6 7 8 9];
исключая элемент с индексом 5. Такую программу можно записать следующим образом:
S = 0; % начальное значение суммы
a = [1 2 3 4 5 6 7 8 9]; % массив
i=0; % счетчик индексов массива
while i < length(a) % цикл (работает пока i меньше
% длины массива а)
i=i+1; % увеличивается счетчик индексов на 1
if i == 5 % если индекс равен 5
continue; % то его не подсчитываем
end
S=S+a(i); % подсчитывается сумма элементов
end % конец цикла
disp(S); % отображение суммы 40 на экране
Следует отметить, что в данной программе увеличение индекса массива i происходит до проверки условия. Это сделано для того, чтобы значение индекса увеличивалось на 1 на каждой итерации работы цикла. Если увеличение счетчика i записать как в предыдущих примерах, т.е. после подсчета суммы, то из-за оператора continue его значение остановилось бы на 5 и цикл while работал бы «вечно».
5.3. Оператор цикла for
Часто при организации цикла требуется перебирать значение счетчика в заданном диапазоне значений и с заданным шагом изменения. Например, чтобы перебрать элементы вектора (массива), нужно организовать счетчик от 1 до N с шагом 1, где N – число элементов вектора. Чтобы вычислить сумму ряда, также задается счетчик от a до b с требуемым шагом изменения step. И так далее. В связи с тем, что подобные задачи часто встречаются в практике программирования, для их реализации был предложен свой оператор цикла for, который позволяет проще и нагляднее реализовывать цикл со счетчиком.
Синтаксис оператора цикла for имеет следующий вид:
for <счетчик> = <начальное значение>:<шаг>:<конечное значение>
<операторы цикла>
end
Рассмотрим работу данного цикла на примере реализации алгоритма поиска максимального значения элемента в векторе:
a = [3 6 5 3 6 9 5 3 1 0];
m = a(1); % текущее максимальное значение
for i=1:length(a) % цикл от 1 до конца вектора с
% шагом 1 (по умолчанию)
if m < a(i) % если a(i) > m,
m = a(i); % то m = a(i)
end
end % конец цикла for
disp(m);
В данном примере цикл for задает счетчик i и меняет его значение от 1 до 10 с шагом 1. Обратите внимание, что если величина шага не указывается явно, то он берется по умолчанию равным 1.
В следующем примере рассмотрим реализацию алгоритма смещения элементов вектора вправо, т.е. предпоследний элемент ставится на место последнего, следующий – на место предпоследнего, и т.д. до первого элемента:
a = [3 6 5 3 6 9 5 3 1 0];
disp(a);
for i=length(a):-1:2 % цикл от 10 до 2 с шагом -1
a(i)=a(i-1); % смещаем элементы вектора а
end % конец цикла for
disp(a);
Результат работы программы
3 6 5 3 6 9 5 3 1 0
3 3 6 5 3 6 9 5 3 1
Приведенный пример показывает, что для реализации цикла со счетчиком от большего значения к меньшему, нужно явно указывать шаг, в данном случае, -1. Если этого не сделать, то цикл сразу завершит свою работу и программа будет работать некорректно.
6. Решения уравнения 6.1. Графический метод решения уравнений
Вывод на экран сразу нескольких графиков предоставляет простейший способ найти приблизительное значение решения.
На данном графике представлены графики функций y=sin(t)/t и (x/5)2+y2=1. Как не трудно заметить данные функции имеют три точки пересечения.
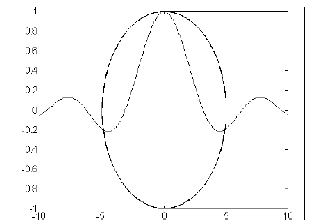
6.2. Поиск решения уравнения
Графическим методом можно лишь примерно оценить решение. Для более точного нахождения решения в пакете MatLAB необходимо воспользоваться функцией fsolve(уравнение, начальное значение). Позже мы познакомимся как с помощью данной функции решать системы уравнений. В простейшем случае решаемое уравнение можно указать можно указать в одинарных кавычках, например: 'x*x-abs(x)'. Но данная функция имеет три решения, представленных на рис.
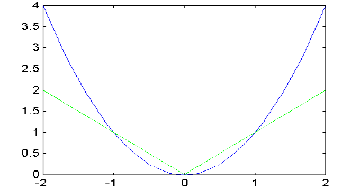
Решение, которое найдет в этом случае функция fsolve будет определяться начальным значением откуда она начнет итерационную процедуру поиска решения. Например:
fsolve('x*x-abs(x)',-2), ans = -1.0000;
fsolve('x*x-abs(x)',0.6), ans = 1.0000;
fsolve('x*x-abs(x)',0.4), ans = 7.9062e-008.
Функция fsolve продолжает итерационную процедуру до тех пор пока она не найдет решение с заданной точностью. По этому в нашем примере мы и получили 7.9062e-008 а не 0.
В случае более сложных функций их удобнее представить в виде M файла. Тогда в качестве первого параметра функции fsolve подставляется в одинарных кавычках имя этого файла.
7. М-файлы
7.1. M-file
Работа из командной строки MatLab затрудняется, если требуется вводить много команд и часто их изменять. Ведение дневника при помощи команды diary и сохранение рабочей среды незначительно облегчают работу. Самым удобным способом выполнения групп команд MatLab является использование М-файлов, в которых можно набирать команды, выполнять их все сразу или частями, сохранять в файле и использовать в дальнейшем. Для работы с М-файлами предназначен редактор М-файлов. С его помощью можно создавать собственные функции и вызывать их, в том числе и из командного окна.
Раскройте меню File основного окна MatLab и в пункте New выберите подпункт M-file. Новый файл открывается в окне редактора M-файлов, которое изображено на рисунке.

М-файлы в MatLab бывают двух типов: файл-программы (Script M-Files), содержащие последовательность команд, и файл-функции, (Function M-Files), в которых описываются функции, определяемые пользователем.
7.2. Файл-программа
Наберите в редакторе команды, приводящие к построению двух графиков на одном графическом окне
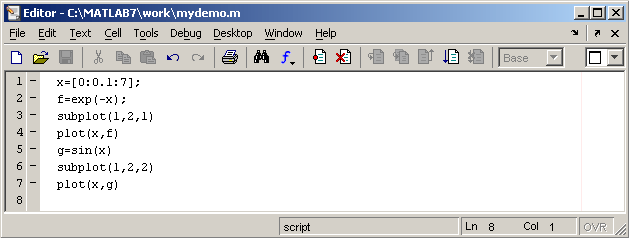
Сохраните теперь файл с именем mydemo.m в подкаталоге work основного каталога MatLab, выбрав пункт Save as меню File редактора. Для запуска на выполнение всех команд, содержащихся в файле, следует выбрать пункт Run в меню Debug. На экране появится графическое окно Figure 1, содержащее графики функций.
Очень удобной возможностью, предоставляемой редактором М-файлов, является выполнение части команд. Закройте графическое окно Figure 1. Выделите при помощи мыши, удерживая левую кнопку, или клавишами со стрелками при нажатой клавише Shift, первые четыре команды и выполните их из пункта Text. Обратите внимание, что в графическое окно вывелся только один график, соответствующий выполненным: командам. Запомните, что для выполнения части команд их следует выделить и нажать клавишу F9.
Отдельные блоки М-файла можно снабжать комментариями, которые пропускаются при выполнении, но удобны при работе с М-файлом. Комментарии начинаются со знака процента и автоматически выделяются зеленым цветом, например:

Открытие существующего М-файла производится при помощи пункта Open меню File рабочей среды, либо редактора М-файлов.
7.3. Файл-функция
М-функции являются M-файлами, которые допускают наличие входных и выходных аргументов. Они работают с переменными в пределах собственной рабочей области, отличной от рабочей области системы MATLAB.
Пример_Функция_average_-_это_достаточно_простой_M-файл,_который_вычисляет_среднее_значение_элементов_вектора:_function_y_=_average_(x)'>Пример
Функция average - это достаточно простой M-файл, который вычисляет среднее значение элементов вектора:
function y = average (x)
% AVERAGE Среднее значение элементов вектора.
% AVERAGE(X), где X - вектор. Вычисляет среднее значение элементов вектора.
% Если входной аргумент не является вектором, генерируется ошибка.
[m,n] = size(x);
if (
((m == 1) | (n == 1)) | (m == 1 & n == 1))
error('Входной массив должен быть вектором’)
end
y =sum(x)/length(x); % Собственно вычисление
Попробуйте ввести эти команды в M-файл, именуемый average.m. Функция average допускает единственный входной и единственный выходной аргументы. Для того чтобы вызвать функцию average, надо ввести следующие операторы:
z = 1:99;
average(z)
ans = 50
Структура М-функции. M-функция состоит из:
строки определения функции;
первой строки комментария;
собственно комментария;
тела функции;
строчных комментариев;
Строка определения функции. Строка определения функции сообщает системе MATLAB, что файл является М-функцией, а также определяет список входных аргументов.
Пример
Строка определения функции average имеет вид:
function y = average(x)
Здесь:
function - ключевое слово, определяющее М-функцию;
y - выходной аргумент;
average - имя функции;
x - входной аргумент.
Каждая функция в системе MATLAB содержит строку определения функции, подобную приведенной.
Если функция имеет более одного выходного аргумента, список выходных аргументов помещается в квадратные скобки. Входные аргументы, если они присутствуют, помещаются в круглые скобки. Для отделения аргументов во входном и выходном списках применяются запятые.
Пример
function [x, y, z] = sphere(theta, phi, rho)
Имена входных переменных могут, но не обязаны совпадать с именами, указанными в строке определения функции.
Первая строка комментария. Для функции average первая строка комментария выглядит так:
% AVERAGE Среднее значение элементов вектора
Это - первая строка текста, которая появляется, когда пользователь набирает команду help <имя_функции>. Кроме того, первая строка комментария выводится на экран по команде поиска lookfor. Поскольку эта строка содержит важную информацию об M-файле, она должна быть тщательно составлена.
Имена М-функций. В системе MATLAB на имена М-функций налагаются те же ограничения, что и на имена переменных - их длина не должна превышать 31 символа. Более точно, имя может быть и длиннее, но система MATLAB принимает во внимание только первые 31 символ. Имена М-функций должны начинаться с буквы; остальные символы могут быть любой комбинацией букв, цифр и подчеркиваний.
Имя файла, содержащего М-функцию, составляется из имени функции и расширения “.m”.
Пример
average.m
Если имя файла и имя функции в строке определения функции разные, то используется имя файла, а внутреннее имя игнорируется. Хотя имя функции, определенное в строке определения функции, может и не совпадать с именем файла, настоятельно рекомендуется использовать одинаковые имена. |
|
|
 Скачать 494 Kb.
Скачать 494 Kb.