MatLab Руководство для начинающих. Matlab сокращение от англ. Matrix Laboratory
 Скачать 494 Kb. Скачать 494 Kb.
|
2.2. Доступ к элементамДоступ к элементам матриц осуществляется при помощи двух индексов — номеров строки и столбца, заключенных в круглые скобки, например команда B(2,3) выдаст элемент второй строки и третьего столбца матрицы B. Для выделения из матрицы столбца или строки следует в качестве одного из индексов использовать номер столбца или строки матрицы, а другой индекс заменить двоеточием. Например, запишем вторую строку матрицы A в вектор z 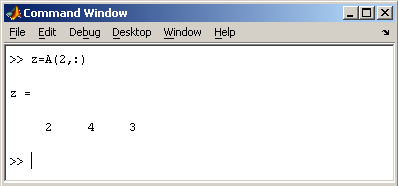 Также можно осуществлять выделение блоков матриц при помощи двоеточия. Например, выделим из матрицы P блок отмеченный цветом 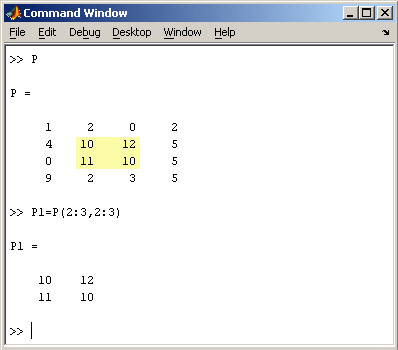 Если необходимо посмотреть переменные рабочей среды, в командной строке необходимо набрать команду whos. Команда who выводит только имена переменных 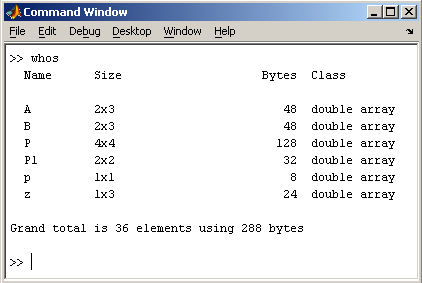 Видно, что в рабочей среде содержатся один скаляр (p), четыре матрицы (A, B, P, P1) и вектор-строка (z). 2.3. Основные матричные операцииПри использовании матричных операций следует помнить, что для сложения или вычитания матрицы должны быть одного размера, а при перемножении число столбцов первой матрицы обязано равняться числу строк второй матрицы. Сложение и вычитание матриц, так же как чисел и векторов, осуществляется при помощи знаков плюс и минус 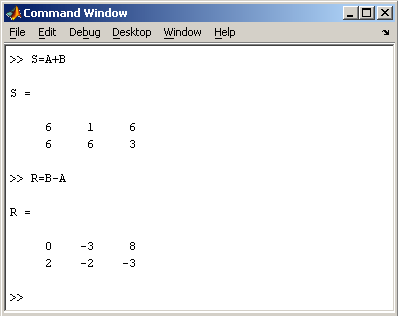 а умножение — знаком звездочка *. Введем матрицу размером 3×2 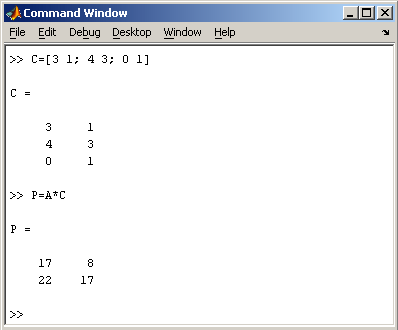 Умножение матрицы на число тоже осуществляется при помощи звездочки, причем умножать на число можно как справа, так и слева. Возведение квадратной матрицы в целую степень производится с использованием оператора ^ 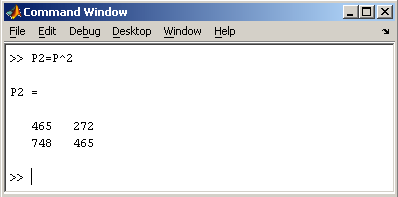 2.4. Создание матриц специального видаЗаполнение прямоугольной матрицы нулями производится встроенной функцией zeros 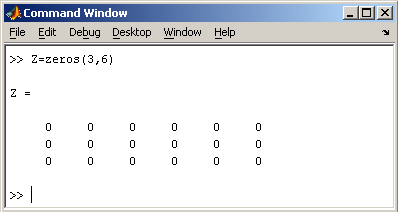 Единичная матрица создается при помощи функции eye 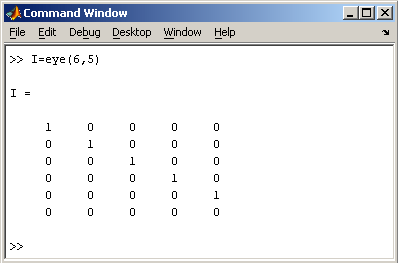 Матрица, состоящая из единиц, образуется в результате вызова функции ones 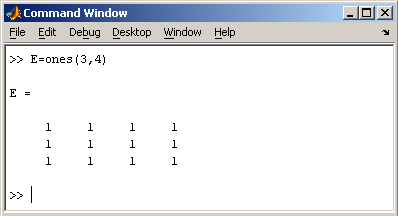 MatLab предоставляет возможность заполнения матриц случайными числами. Результатом функции rand является матрица чисел, равномерно распределенных между нулем и единицей, а функции randn — матрица чисел, распределенных по нормальному закону с нулевым средним и единичной дисперсией. Функция diag формирует диагональную матрицу из вектора, располагая элементы по диагонали. Пример. Команда z = magic(3) генерирует магический квадрат размера 3 x 3 2.5. Матричные вычисленияMatLab содержит множество различных функций для работы с матрицами. Так, например, транспонирование матрицы производится при помощи апострофа ' 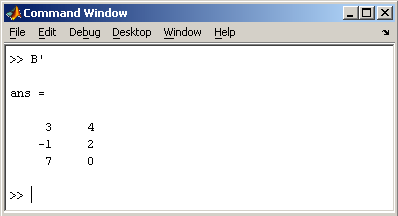 Нахождение обратной матрицы проводится с помощью функции inv для квадратных матриц 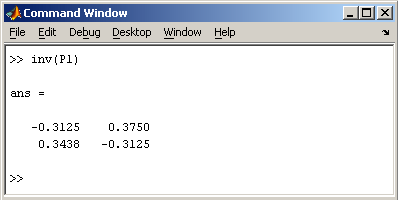 Псевдообратную матрицу можно найти с помощью функции pinv. Более подробно про обработку матричных данных можно узнать, если вывести список всех встроенных функций обработки данных командой help datafun, а затем посмотреть информацию о нужной функции, например help max. 2.6. Справочник по формированию и операциям над матрицамиФормирование массивов специального вида
Операции над матрицами
Специальные матрицы
2.7. Присвоение матрице математического выраженияОрганизация всех переменных системы MATLAB как матрицы вызывает следующие ограничения применения их в выражениях. Например: t=1:5 t= 1 2 3 4 5 y=cos(t) y=1 0.5 -0.4 -1 -0.6 0.2 z=y/t z=-0.08 Результат - получается одно число, а ожидали функцию z(t)=cos(t)/t. Для организации поэлементного деления одного массива на другой, в MATLAB предусмотрена специальная операция - «./» - поэлементное деление. Результат этого выражения будет другой: z=y ./ t z= 0.5403 -0.2081 -0.3300 -0.1634 0.0567. 3. Математические функции В системе MATLAB имеется обширная библиотека математических функций. Каждой функции соответствует определенное имя. Функция ставит в соответствие значениям своих аргументов значение результата. Аргументы функции всегда указываются в круглых скобках после имени функции и, если их больше одного, разделяются запятыми. В качестве аргументов могут использоваться другие функции и любые выражения языка MATLAB (при условии соответствия типов аргументов). Элементарная математическая функция - это, как правило, функция от одной переменной, и в этом случае устанавливается соответствие между массивами значений аргумента и результата. Аргумент указывается в круглых скобках после имени функции. Имя переменной, которой присваивается значение функции, располагается слева от знака равенства. Если имя присваиваемой переменной не указано, значение функции присваивается служебной переменной ans. Тип результата вычисления математической функции всегда совпадает с типом ее аргумента. Например, если аргументом функции является вектор-столбец, то значением этой функции также будет вектор-столбец. Рассмотрим встроенные математические функции системы MATLAB, которые применяются к числам, скалярным переменным и к массивам (поэлементно). Базовые функции
Трансцендентные функции
Тригонометрические функции
Преобразования системы координат
Специальные функции
|
