Матрицы. Обратные матрицы
 Скачать 274.72 Kb. Скачать 274.72 Kb.
|
|
1 #23 *! Қисықтармен шектелген фигураның ауданы #24 *! Қисық доғасының ұзындығы #25 *! 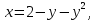 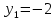 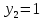 түзулерімен шектелген фигураның ауданы түзулерімен шектелген фигураның ауданы 4,5=4,1/2 #26 *! 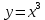 , , 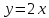 түзулерімен шектелген фигураның ауданы түзулерімен шектелген фигураның ауданы 2 #27 *! 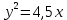 , , 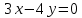 түзулерімен шектелген фигураның ауданы түзулерімен шектелген фигураның ауданы 8 #28 *! 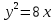 , 2 , 2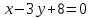 түзулерімен шектелген фигураның ауданы түзулерімен шектелген фигураның ауданы 3/4 #29 *! 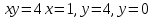 түзулерімен шектелген айналу денесінің көлемі түзулерімен шектелген айналу денесінің көлемі 12П #30 *! Меншіксіз интегралды есептеңіз 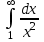 1 #31 *! y 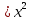 , , 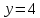 x=0 түзулерімен шектелген фигураның ауданы x=0 түзулерімен шектелген фигураның ауданы 16/3=5,3/1 *! y 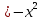 , , 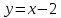 y=0 түзулерімен шектелген фигураның ауданы y=0 түзулерімен шектелген фигураның ауданы #33 *! y 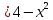 , , 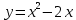 түзулерімен шектелген фигураның ауданы түзулерімен шектелген фигураның ауданы #34 *! y 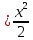 , , 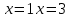 түзулерімен шектелген фигураның ауданы түзулерімен шектелген фигураның ауданы #35 *! y 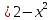 , , 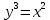 түзулерімен шектелген фигураның ауданы түзулерімен шектелген фигураның ауданы #36 *! Меншіксіз интегралды есептеңіз 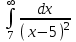 #1 *! 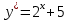 дифференциалдық теңдеуінің шешімі: дифференциалдық теңдеуінің шешімі:2xln2+5x+C #2 *! 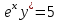 дифференциалдық теңдеуінің шешімі: дифференциалдық теңдеуінің шешімі:Y(x)=C 1 +5e-x *! xdy=5ydx дифференциялдық теңдеуінің дербес шешімін табыңыз, егер x=1 болғанда y=-1болса X=-X5 #4 *! 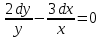 , диф. теңдеуінің дербес шешімін табыңыз, егер х=1 болғанда , диф. теңдеуінің дербес шешімін табыңыз, егер х=1 болғанда 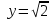 болса болсаY2 =CX3 #5 *! Берілген теңдеулердің арасынан айнымалылары ажыратылатын диф. теңдеуді көрсетіңіз: #6 *! x=5, y=15 мәнiндегi xdy=ydx теңдеуiнiң шешiмiн табыңыз: Y=3x #7 *! 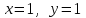 болғандағы, болғандағы, 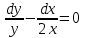 дербес шешiмiн табыңыз: дербес шешiмiн табыңыз:Y=C түбір асты Х (тубрды таппай калдым) #8 *!Айнымалылары ажыратылатын теңдеудi көрсетiңiз: #9 *! 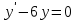 дифференциалдық теңдеуiнiң шешiмi: дифференциалдық теңдеуiнiң шешiмi:Y(x)=C1e6x #10 *! 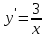 дифференциалдық теңдеудiң шешiмi: дифференциалдық теңдеудiң шешiмi:Y(x)=C1+3log(x) # 11 *!Коши есебі: +ізделінді функцияның бастапқы берілуі #12 *! Айнымалылары ажыратылған диф.теңдеу мына түрде жазылады: #13 *! 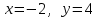 болғандағы, болғандағы,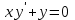 дифференциалдық теңдеуiнiң дербес шешiмiн табыңыз: xy+y=0 дифференциалдық теңдеуiнiң дербес шешiмiн табыңыз: xy+y=0#14 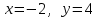 болғандағы, болғандағы, 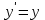 дифференциалдық теңдеуiнiң дербес шешiмiн табыңыз: y=4ex+2 дифференциалдық теңдеуiнiң дербес шешiмiн табыңыз: y=4ex+2#1 *!Дифференциалдық теңдеу деп.....байланыстыратын қатынасты айтады + х тәуелсіз айнымалыны, у(х) ізделінді функцияны және оның әртүрлі реттегі туындыларын #2 *!Ізделінді функция бір айнымалыдан тәуелді болса, онда дифференциалдық теңдеу.....деп аталады: +Қарапайым дифференциалдық теңдеу #3 *! Pdx+Qdy=0 түріндегі теңдеу, мұндағы P және Q - x және y тәуелді бірдей дәрежелі біртекті функциялар +бірінші ретті біртекті дифференциалдық теңдеу #4 *! Дифференциалдық теңдеудің реті +туындының жоғарғы ретін #5 *!Жалпы шешімнен 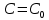 мәніне тең болғанда алынған мәніне тең болғанда алынған 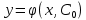 функциясы функциясы *+ #6 *!Коши есебі дегеніміз... +бастапқы шарттарды қанағаттандыратын дифференциалдық теңдеудің дербес шешімін табу #7 *!Айнымалылары ажыратылған дифференциалдық теңдеу + 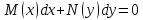 #8 *!Бiрiншi реттi сызықтық дифференциалдық теңдеу + #9 *! #10 *!1-ші ретті біртекті сызықтық дифференциалдық теңдеудің жалпы шешімі *+ 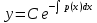 #11 *!Дифференциалдық теңдеудің жалпы түрі #12 *!Бірінші ретті дифференциалдық теңдеудің жалпы шешімі 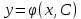 #13 *! Толық дифференциалды M(x,y)dx+N(x,y)dy=0 теңдеуінің жалпы интегралы + 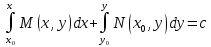 #14 *!n-ші ретті дифференциалдық теңдеу + 1. Дифференциалдық сызықтық біртекті теңдеудің түрі 2. 1-ретті сызықтық біртекті емес дифференциалдық теңдеу *+у/-2у/х=2х3 3. 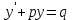 түрiндегi теңдеу атауы, мұндағы p және q-функциялары x тәуелдi немесе тұрақты шамалар түрiндегi теңдеу атауы, мұндағы p және q-функциялары x тәуелдi немесе тұрақты шамалар4. Сызықтық біртекті 1-ретті дифференциалдық теңдеудің жалпы шешімі 5. Сызықтық біртекті емес 1-ретті дифференциалдық теңдеудің жалпы шешімі 6. Сызықтық біртекті емес 1-ретті дифференциалдық теңдеудің шешудің әдісі 7. 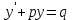 дифференциалдық теңдеудің шешудің әдісі дифференциалдық теңдеудің шешудің әдісі8. Қай әдіспен 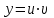 алмастыру арқылы сызықтық біртекті емес 1-ретті дифференциалдық теңдеудің шешімін іздейміз? алмастыру арқылы сызықтық біртекті емес 1-ретті дифференциалдық теңдеудің шешімін іздейміз?9. Бернулли әдісінде 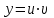 алмастыруда u функциясы алмастыруда u функциясы10. Бернулли әдісінде 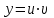 алмастыруда v функциясы алмастыруда v функциясы11. 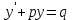 дифференциалдық теңдеудің дифференциалдық теңдеудің 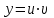 алмастыруда v функциясының шешімі алмастыруда v функциясының шешімі12. 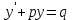 дифференциалдық теңдеудің дифференциалдық теңдеудің 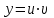 алмастыруда u функциясының шешімі алмастыруда u функциясының шешімі13. 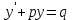 дифференциалдық теңдеудің Лагранж әдісінің басқа атауы дифференциалдық теңдеудің Лагранж әдісінің басқа атауы14. 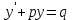 дифференциалдық теңдеудің p, q ______ функциялар дифференциалдық теңдеудің p, q ______ функциялар15. Сызықты біртекті дифференциалдық теңдеу 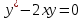 y=Cx2 y=Cx216. Сызықты біртекті емес дифференциалдық теңдеу 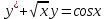 17. Сызықтық дифференциалдық теңдеу 18. Берілген дифференциалдық теңдеулердің қайсысы бірінші ретті сызықтық теңдеу болады 19. y-yctgx=2xsinx теңдеуді шешіңіз 20. 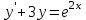 теңдеуінің p(x), q(x)-? теңдеуінің p(x), q(x)-?21. xdx+ydy=0 теңдеудi шешіңіз 22. 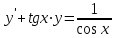 теңдеудi шешіңіз теңдеудi шешіңіз23. 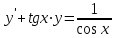 теңдеуінің p(x), q(x)-? теңдеуінің p(x), q(x)-?24. 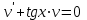 теңдеудi шешіңіз теңдеудi шешіңіз25. у'-2у/х=х2 теңдеудi шешіңіз 26. у'-2у/х=2х теңдеуінің p(x), q(x)-? 27. у'-2у/х=0 теңдеудi шешіңіз 28. у'+у/х=х теңдеуінің p(x), q(x)-? #1 *!2-ші ретті дифференциалдық теңдеу 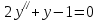 #2 *!3-ші ретті дифференциалдық теңдеу + 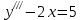 *!2-ші ретті дифференциалдық теңдеу + 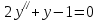 #4 *! #5 *! #6 *! #7 *! 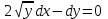 дифференциалдық теңдеудің шешу әдісі дифференциалдық теңдеудің шешу әдісі #8 *!Төменде көрсетілгендердің қайсысы «Коши есебі» болып табылады... #9 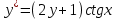 дифференциалдық теңдеуді дифференциалдық теңдеуді 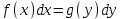 түріне келтір түріне келтір#10 *! 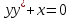 дифференциалдық теңдеуді дифференциалдық теңдеуді 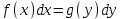 түріне келтір түріне келтір#11 *! 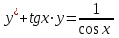 сызықты дифференциалдық теңдеудің p(x) және g(x) функцияларын анықтау керек сызықты дифференциалдық теңдеудің p(x) және g(x) функцияларын анықтау керек 15 #13*! 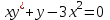 сызықты дифференциалдық теңдеудің p(x) және g(x) функцияларын анықтау керек сызықты дифференциалдық теңдеудің p(x) және g(x) функцияларын анықтау керек +p(x)= 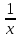 g(x)=3x g(x)=3x#14*! Дифференциалдық теңдеудің жалпы шешімі 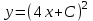 және бастапқы шартты және бастапқы шартты 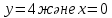 белгілі болса, онда С неге тең белгілі болса, онда С неге тең +с=2 #15*! Дифференциалдық теңдеудің жалпы шешімі 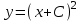 және бастапқы шартты және бастапқы шартты 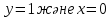 белгілі болса, онда С неге тең белгілі болса, онда С неге тең +с=1 #16*! Дифференциалдық теңдеудің реті *+туындының жоғарғы ретін #17*!Дифференциалдық теңдеудің орнына қойғанда оны теңбе-теңдікке айналдыратын кез-келген функция... +дифференциалдық теңдеудің шешімі #18*!Бірінші ретті дифференциалдық теңдеудің жалпы шешімі *+ 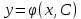 #19*!Коши есебі: *+ тәуелсіз айнымалының бастапқы берілуі #20*! +айнымалылары ажыратылатын дифференциалдық теңдеу #21*! 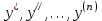 - олардың туындылары - олардың туындылары+*+n-ші ретті дифференциалдық теңдеу #22*!n-ші ретті дифференциалдық теңдеу + #23*! 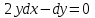 дифференциалдық теңдеудің шешу әдісі дифференциалдық теңдеудің шешу әдісі +айнымалыларын ажырату #24*!Төменде көрсетілгендердің қайсысы «Коши есебі» болып табылады... + #25 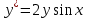 дифференциалдық теңдеуді дифференциалдық теңдеуді 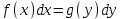 түріне келтір түріне келтір+ 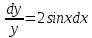 #26*! 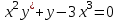 сызықты дифференциалдық теңдеудің p(x) және g(x) функцияларын анықтау керек сызықты дифференциалдық теңдеудің p(x) және g(x) функцияларын анықтау керек +p(x)= 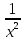 g(x)=3x g(x)=3x#27*! Дифференциалдық теңдеудің жалпы шешімі 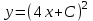 және бастапқы шартты және бастапқы шартты 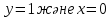 белгілі болса, онда С неге тең белгілі болса, онда С неге тең +c=1 #28*! 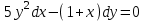 дифференциалдық теңдеудің шешу әдісі дифференциалдық теңдеудің шешу әдісі +айнымалыларын ажырату #29 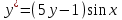 дифференциалдық теңдеуді дифференциалдық теңдеуді 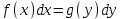 түріне келтір түріне келтір+ 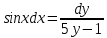 #30*! 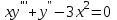 дифференциалдық теңдеуінің реті дифференциалдық теңдеуінің реті+3 #31*! xdy=ydx дифференциялдық теңдеуінің дербес шешімін табыңыз, егер x=1, y=4 болса +y=4x #32*! 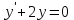 дифференциалдық теңдеуінің шешімі: дифференциалдық теңдеуінің шешімі:+y=C1e-2x или просто y=e-2x С #33*! 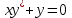 дифференциалдық теңдеуінің шешімі: дифференциалдық теңдеуінің шешімі:+y= 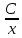 #34*! xdy=ydx дифференциялдық теңдеуінің дербес шешімін табыңыз, егер x=2, y=4 болса +y=2x #35*! Решение уравнения 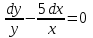 , если х=1 , y=1 , если х=1 , y=1 +y=x5 #36*! Берілген теңдеулердің арасынан айнымалылары ажыратылатын диф. теңдеуді көрсетіңіз: +*!Р(х,у)dх + G(x,y)dy = 0 , #37*! 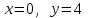 болғандағы, болғандағы, 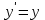 дифференциалдық теңдеуiнiң дербес шешiмiн табыңыз: дифференциалдық теңдеуiнiң дербес шешiмiн табыңыз:+y=4ex #38*! Төменде көрсетілгендердің қайсысы «Коши есебі» болып табылады... + #39 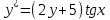 дифференциалдық теңдеуді дифференциалдық теңдеуді 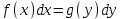 түріне келтір түріне келтір+ 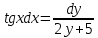 #40*! Дифференциалдық теңдеудің жалпы шешімі 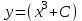 және бастапқы шартты және бастапқы шартты 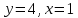 белгілі болса, онда С неге тең белгілі болса, онда С неге тең +C=3 #1*!Алғашқы функцияның дифференциалынан алынған анықталмаған интеграл неге тең *+ 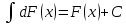 #2*!Егер С – тұрақты сан болса, онда 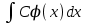 интегралы тең интегралы тең+ 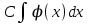 #3*!Функцияның алгебралық қосындысының анықталмаған интегралы *+ 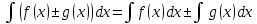 #4*!Егер F(x) функциясының туындысы f(x)-ке тең болса, онда F(x).....деп аталады: +алғашқы функция #5*!Анықталмаған интегралдың дифференциалы тең: +интеграл таңбасының астындағы өрнекке #6*!Егер F(x) функциясы f(x) үшін алғашкы функция болса, онда F(x)+c өрнегі ... деп аталады +Анықталмаған интеграл #7*!Функцияның анықталмаған интегралын есептеу процесi: *+интегралдау #8 *! 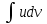 = =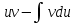 #9 *! 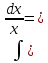 lnx+c lnx+c#10 *! 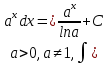 #11 *! 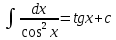 #12 *! 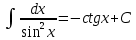 #13 *! 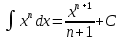 #14 *! 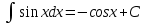 #1 *! 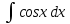 интегралы үшін интегралдау әдісі интегралы үшін интегралдау әдісі+тікелей #2 *!n-нiң қандай мәнiнде 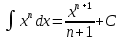 орындалмайды орындалмайды+n=-1 #3 *!Анықталмаған интеграл үшін бөліктеп интегралдау формуласы: *+ 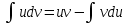 #4 *! 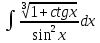 интегралы үшін интегралдау әдісі интегралы үшін интегралдау әдісі*+айнымалыны алмастыру әдісі ,дифференциал танбасына енгизу #5 *! 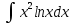 интегралындағы u және dv интегралындағы u және dv *+ 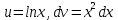 #6 *! 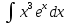 интегралындағы u және dv интегралындағы u және dv*+ 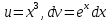 #7 *! +тікелей #8 *!Тікелей интегралдау әдісімен есептелетін интеграл +варианттан коресиндер гой #9 *! 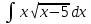 интегралы үшін интегралдау әдісі интегралы үшін интегралдау әдісі *+айнымалыны алмастыру әдісі #10*! 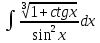 интегралы үшін интегралдау әдісі интегралы үшін интегралдау әдісі*+айнымалыны алмастыру әдісі #11 *! 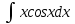 интегралы үшін интегралдау әдісі интегралы үшін интегралдау әдісі*+бөліктеп интегралдау әдісі #12 *!Айнымалыны алмастыру әдісімен есептелетін интеграл +*! 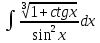 бул жай пример бул жай пример#13 *!Бөліктеп интегралдау әдісімен есептелетін интеграл + 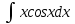 тоже пример тоже пример#14 *! 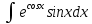 интегралдауда қолданылатын алмастыру интегралдауда қолданылатын алмастыру*+t=cosx #1*! 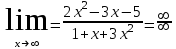 . Берілген шекті шешу әдісі . Берілген шекті шешу әдісі +x2 жақша сыртына шығару немесе x2 қа бөлу #2*! 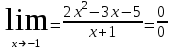 . Берілген шекті шешу әдісі . Берілген шекті шешу әдісі +үстін түрлендіресің #3 *! 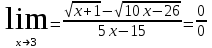 . Берілген шекті шешу әдісі . Берілген шекті шешу әдісі +түйіндісіне бөліп көбейту болу керек, үстін көбейтіп бөлесіндер ғой #4*! 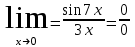 . Берілген шекті шешу әдісі . Берілген шекті шешу әдісі+1 тамаша шек #5*! 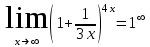 . Берілген шекті шешу әдісі . Берілген шекті шешу әдісі+2 тамаша шек #6 *!Егер 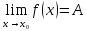 және және 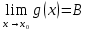 , онда , онда 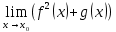 шегі тең шегі тең*+ 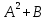 #7 *!Егер 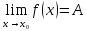 және және 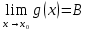 , онда , онда 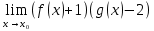 шегі тең шегі тең*+(А+1)(В-2) #8*!Егер 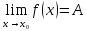 және және 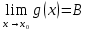 , онда , онда 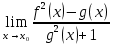 шегі тең шегі тең *+ 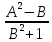 #9*! 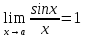 теңдігі дұрыс болатындай а мәнін табыңдар теңдігі дұрыс болатындай а мәнін табыңдар+a=0 #10 *! 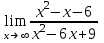 шектің мәні шектің мәні+1 #11*! 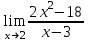 шектің мәні шектің мәні+10 #12*!Егер 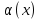 функциясы функциясы 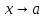 болғанда шексіз аз шама болса, онда f(x)= болғанда шексіз аз шама болса, онда f(x)=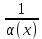 функциясы функциясы+шексіз үлкен шама 25 #13*!(2х-5)dx өрнегі ... функциясының дифференциалына сәйкес 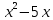 #14*!y = 2x3 - 5x2 +7x +4 функциясының туындысы тең 6x2-10x+7 1. Оқиға- Қандай да бір сынаудың нәтижесінде пайда бола алатын кез келген факті 2. Ықтималдықтың классикалық анықтамасы А оқиғасын тудыруға қолайлы оқиғалар санының сынау нәтижесiнде пайда болулары мүмкiн барлық оқиғалар санына қатынасы 3. Толық топ құрайтын екi үйлесiмсiз оқиға қарама-қарсы 4. Элементар оқиғалар кеңiстiгi Элементар оқиғалардың жиыны 5. А1, А2,…,Аn оқиғаларының кемiнде бiреуiнiң пайда болу ықтималдығы A жәнеB оқиғаларының қосындысы (бірігуі) 6. А және В оқиғаларының көбейтiндiсi екеуінің бірге пайда болуы 7. А және В оқиғаларының қосындысы оқиғаларының кемiнде бiреуiнiң пайда болу ықтималдығы 8. Тәуелсiз оқиғалардың бiрге пайда болу ықтималдығы 9. Тәуелдi оқиғалардың бiрге пайда болу ықтималдығы P(AВ) =P(А) PA(В) 10. Сынау нәтижесiнде мiндеттi түрде пайда болатын оқиға ақиқат 11. А оқиғасы толық топ құрайтын үйлесiмсiз В1, В2, …, Вn оқиғаларының бiрi орындалғанда ғана пайда болады. Бұл оқиғалардың қайсысы орындалатыны алдын ала белгiсiз болғандықтан, олар кездейсоқ 12. Р(А+В) символы ненi бiлдiредi? Егер А мен В оқиғалары қиылыспайтын болса, онда қосындының ықтималдығы ықтималдықтардың қосындысы тең болады 13. Толық ықтималдық формуласы 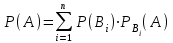 14. Байес формуласы 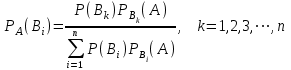 15. "Студент" сөзiнен сәтiне қарай бiр әрiп таңдалды. Таңдалынған әрiптiң дауысты болу ықтималдығы 2/7 16. Жәшiкте 3 қара, 5 ақ, 4 қызыл шар бар. Сәтiне қарай бiр шар алынды. Алынған шардың қызыл емес болуының ықтималдығы неге тең. 2/3 17. Бiр жәшiкте 20 қорап анальгин, 50 қорап цитрамон және 30 қорап кофеин бар. Жәшiктен кездейсоқ қорап алынған. Алынған қораптың цитрамон немесе кофеин болу ықтималдығы 0,8. 18. Жәшiкте 6 ақ, 4 қара шар бар. Кездейсоқ жәшiктен екi шар алынған. Алынған шардың екеуiнiң де ақ болу ықтималдығы 1/3. 19. Екі мерген бір - біріне тәуелсіз нысанаға оқ атты. Бірінші мерген үшін нысанаға дәл тию ықтималдығы 0,7 –ге, екінші үшін 0,8-ге тең. Нысанаға дәл тию ықтималдығы 0,94 20. Екі мерген бір - біріне тәуелсіз нысанаға оқ атты. Бірінші мерген үшін нысанаға дәл тию ықтималдығы 0,7-ге тең, екінші мерген үшін 0,8-ге тең. Екі мергеннің бір мезгілде нысанаға дәл тию ықтималдығы 0,56 21. Екі мерген бір - біріне тәуелсіз нысанаға оқ атты. Бірінші мерген үшін нысанаға дәл тию ықтималдығы 0,7-ге тең, екінші мерген үшін 0,8-ге тең. Тек бір мергеннің нысанаға дәл тию ықтималдығы 0,38 22. Тұмау эпидемиясы кезінде ауруханаға жеткізілген 15 адамның ішіндегі 5-ң аяғы сынған. Палатаға 4 адамнан жатқызды. Жатқызылған адамдардың ішінде кем дегенде біреуінің аяғы сынған болып шығу ықтималдығы 11/13 23. Препараты стандарттылыққа екі фармацевттің бірімен тексеріледі. Препаратың бірінші фармацевтке түсу ықтималдығы 0,55, ал екінші фармацевтке – 0,45. Препаратты бірінші фармацевт стандартты деп қабылдау ықтималдығы 0,9, ал екінші фармацевт – 0,98. Препарат тексеру кезінде стандарты деп қабылданды. Бұл препаратты екінші фармацевт тексергендігінің ықтималдығын табыңыз 0,471 24. Әртүрлі перфораторда перфокарталардың бірдей жиынында екі перфораторшы берді. Бірінші перфораторшының қате жіберу ықтималдығы 0,05 тең, ал екінші перфораторшынікі 0,1 тең. Перфоратты тексеру кезінде қате табылуының ықтималдығын табыңыз 0,075 25. Бірдей формадағы 2 жәшік бар. 1-ші жәшікте 3 ақ, 2 қара, ал 2-ші жәшікте – 4 ақ және 3 қара шар бар. Кездейсоқ кез келген жәшіктен 1 шар алынады. Алынған шар ақ шар. Шар 1-ші жәшіктен алынғандығының ықтималдығын табыңыз. 26. Студент емтиханның 24 сұрағының тек 20–ын біледі. Бір билетте 3 сұрақ бар. Оған ең болмағанда бір дайындалмаған сұрағы бар билет түсу ықтималдығы 221/506 27. Жол апатында 12 адам зардап шекті, оның 4-і аяғын күйдіріп алды. Жедел жәрдем емханаға екі адамнан тасиды. Машинадағы екі адамның да аяғы күйген болып шығу ықтималдығы 1/11 28. Бөлімде 4 палата бар. Түнімен оттегі жастығын қажает ету ықтималдығы бірінші палата үшін – 0,2, екінші - 0,3, үшінші - 0,2, төртінші – 0,1. Түн ішінде екінші немесе үшінші палатаға оттегі жастығының қажет ету болып қалу ықтималдығы 0,5 |
