|
|
Матем. КР1 для психологов. Матрицы. Операции над матрицами
Пример. Решить систему уравнений:
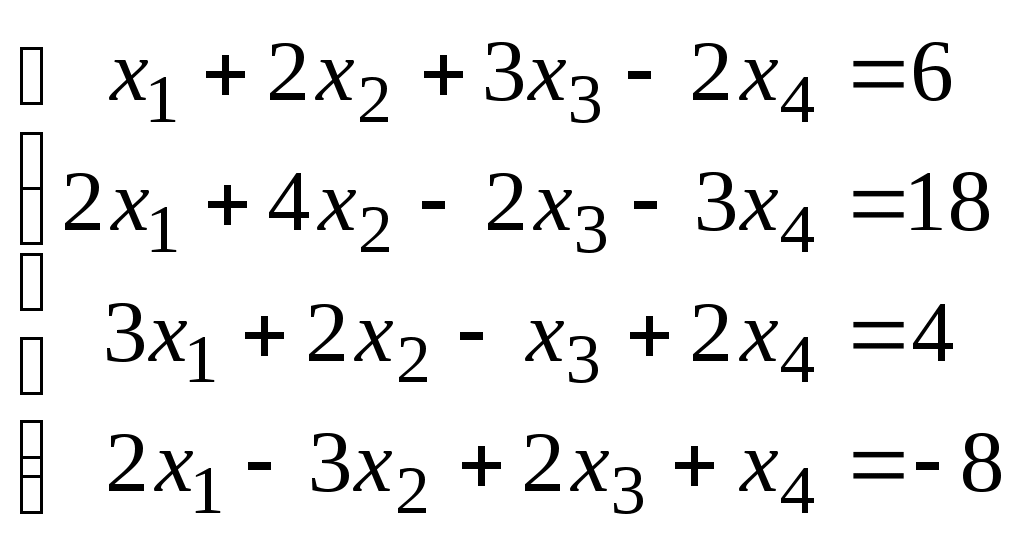 . .
Решение. Расширенная матрица системы имеет вид:
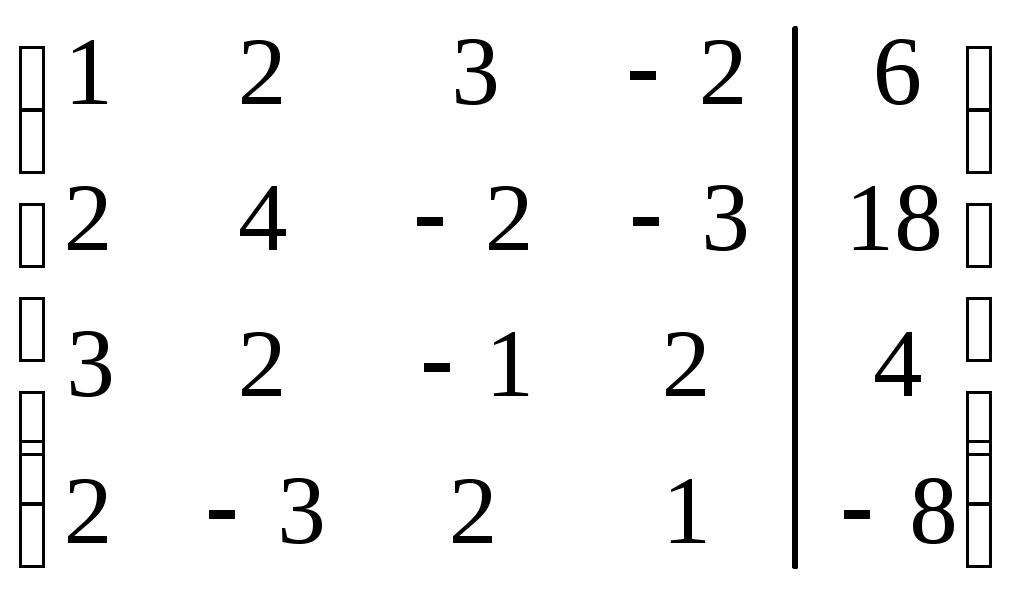 . .
Шаг 1. Так как  , то умножая на вторую, третью и четвертую строки матрицы на числа (-2), (-3), (-2) и прибавляя полученные строки соответственно ко второй, третьей, четвертой строкам, исключим переменную , то умножая на вторую, третью и четвертую строки матрицы на числа (-2), (-3), (-2) и прибавляя полученные строки соответственно ко второй, третьей, четвертой строкам, исключим переменную  из всех строк, начиная со второй. Заметив, что в новой матрице из всех строк, начиная со второй. Заметив, что в новой матрице 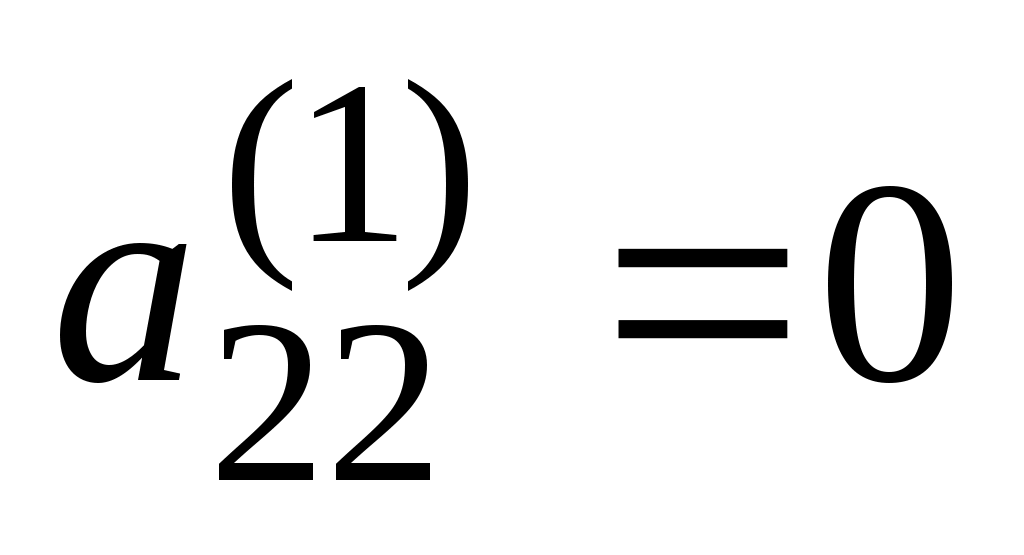 , поменяем местами вторую и третью строки: , поменяем местами вторую и третью строки:
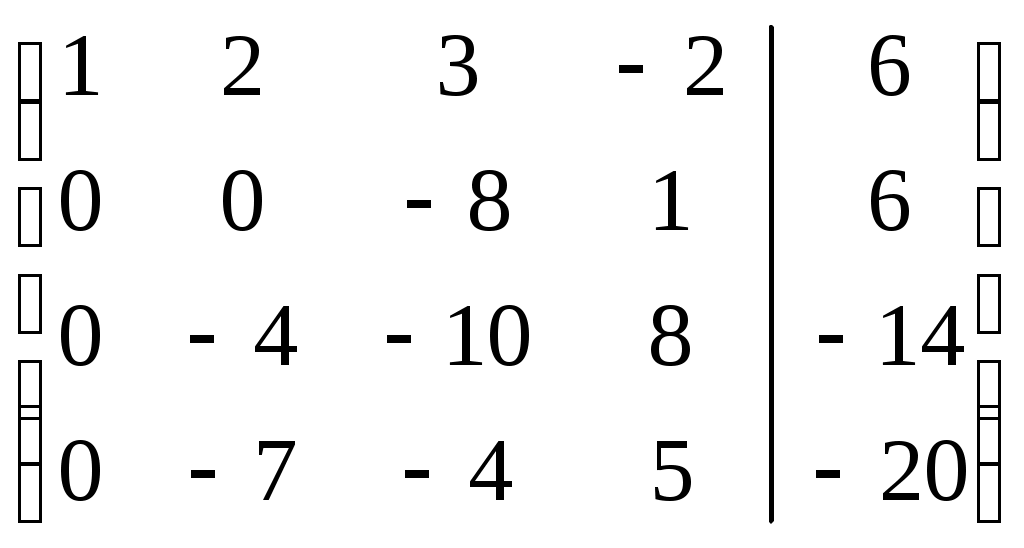  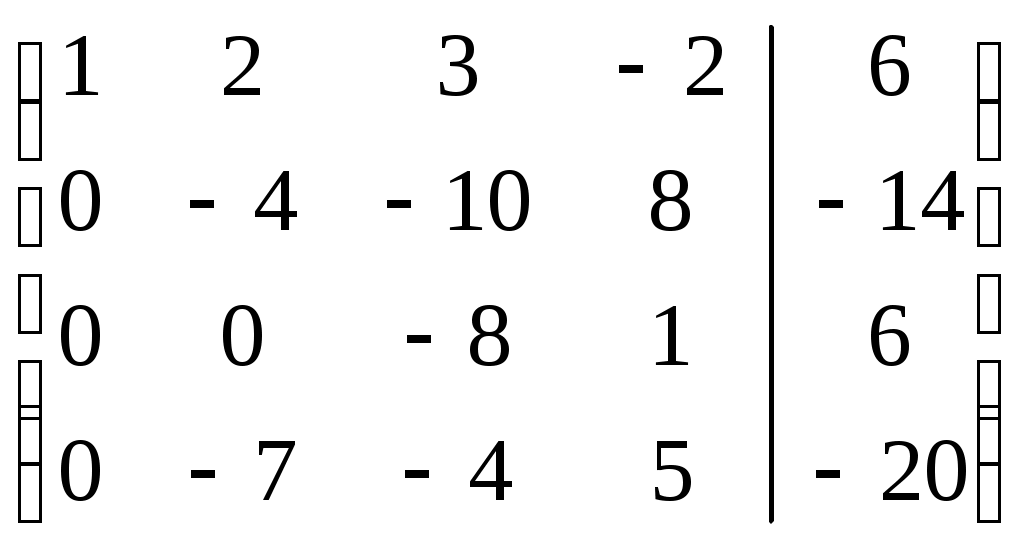 . .
Шаг 2. Так как теперь 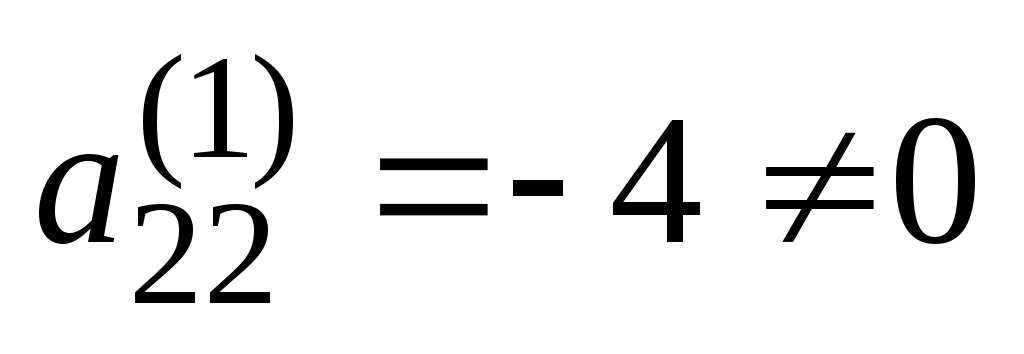 , то умножая вторую строку на (-7/4) и прибавляя полученную строку к четвертой, исключим переменную , то умножая вторую строку на (-7/4) и прибавляя полученную строку к четвертой, исключим переменную  из всех строк, начиная с третьей: из всех строк, начиная с третьей:
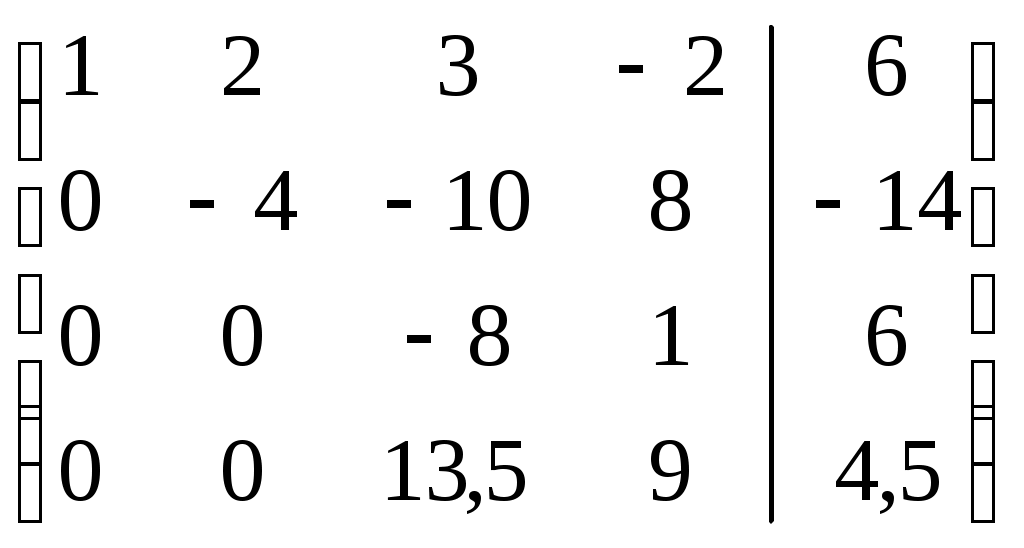  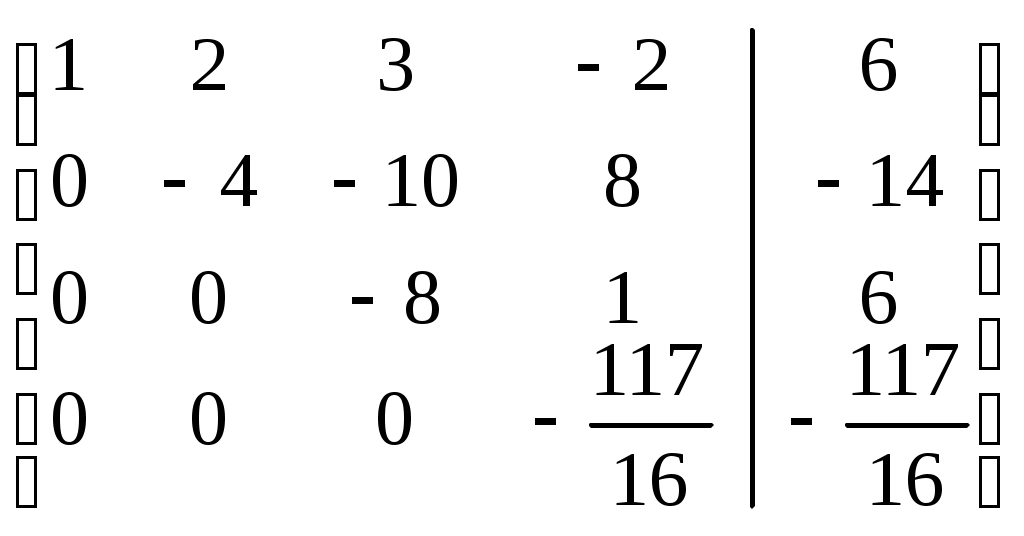 . .
Шаг 3. Учитывая, что 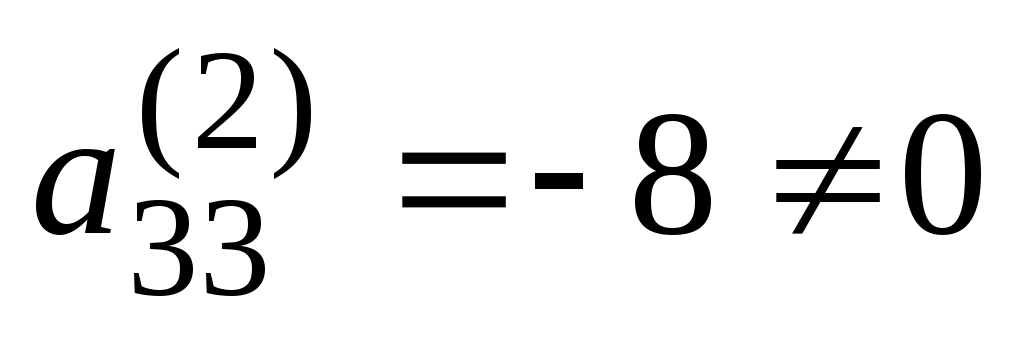 ,умножаем третью строку на 13,5/8=27/16, и прибавляя полученную строку к четвертой, исключим из нее переменную ,умножаем третью строку на 13,5/8=27/16, и прибавляя полученную строку к четвертой, исключим из нее переменную 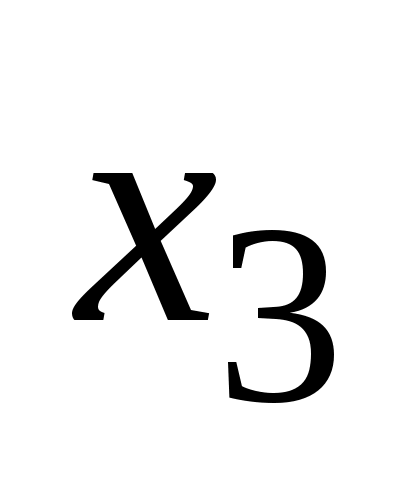 . Получим (см. последнюю матрицу) систему уравнений: . Получим (см. последнюю матрицу) систему уравнений:
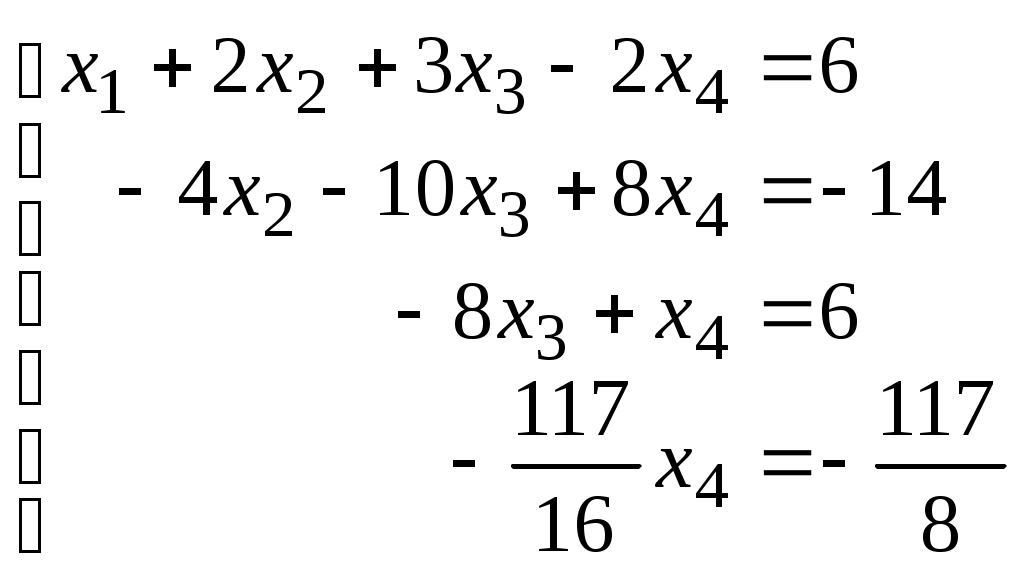 , ,
откуда, используя обратгный ход метода Гаусса, найдем из четвертого уравнения 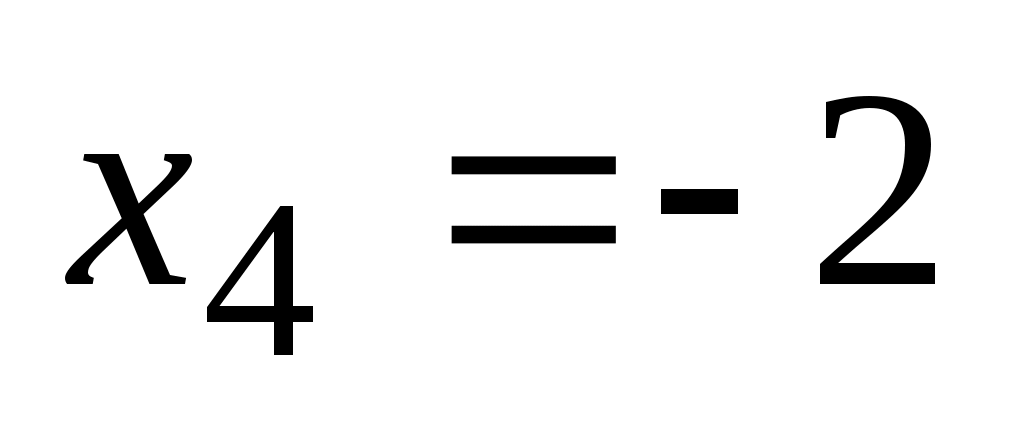 ; из третьего ; из третьего 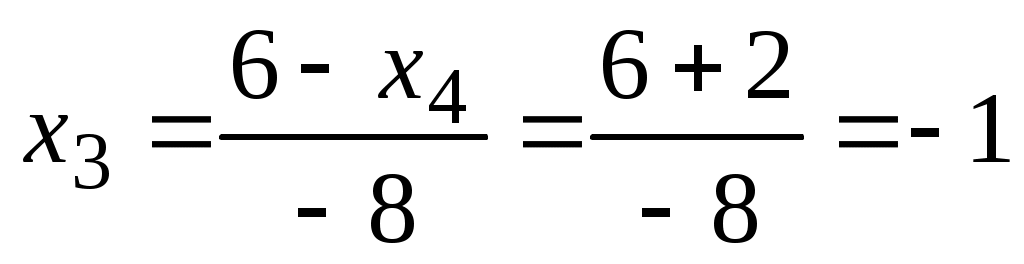 ; из второго ; из второго 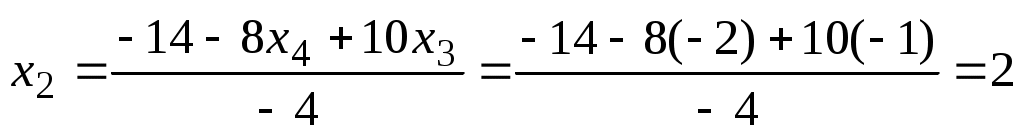 и из первого уравнения и из первого уравнения 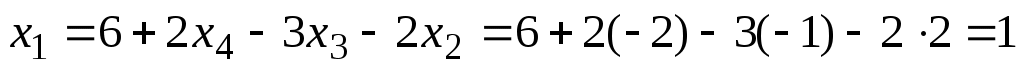 , то есть решение системы (1;2;-1;-2). , то есть решение системы (1;2;-1;-2).
ПРОИЗВОДНАЯ.
Производной функции 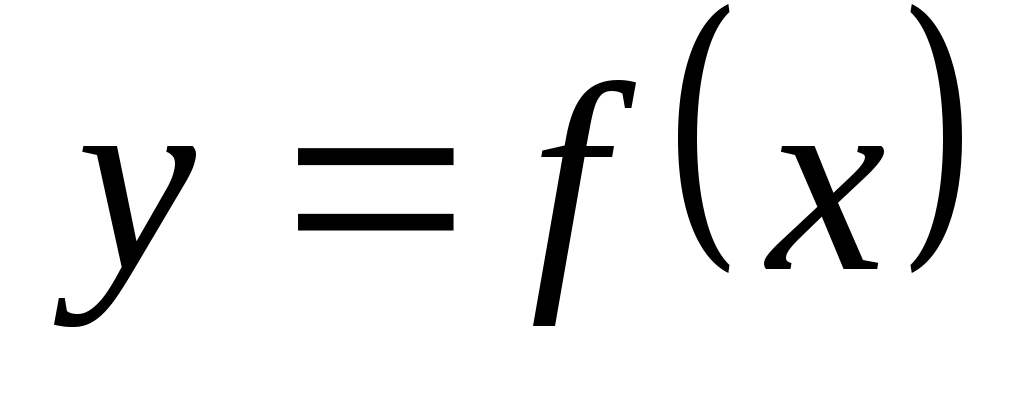 называется придел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю (если этот предел существует: называется придел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю (если этот предел существует:
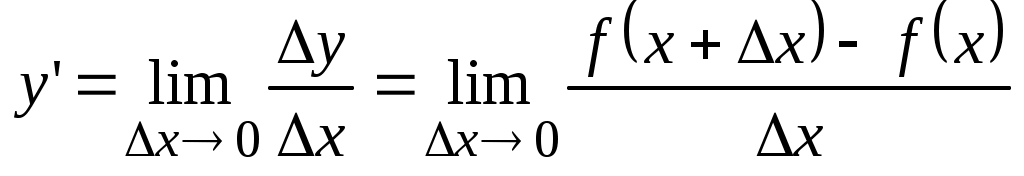 . .
Правила дифференцирования.
Производная постоянной равна нулю:
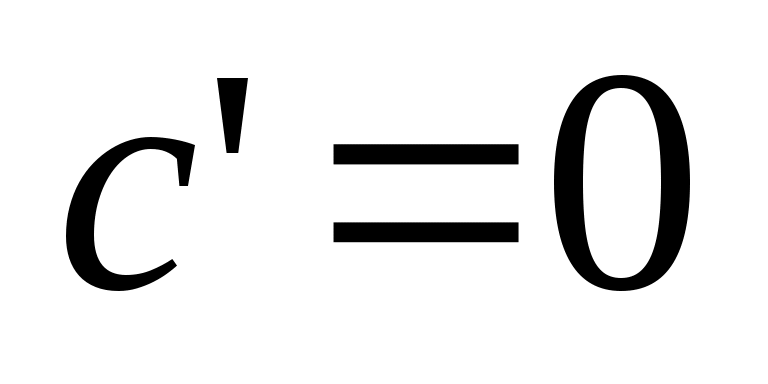 . .
Производная аргумента равна 1:
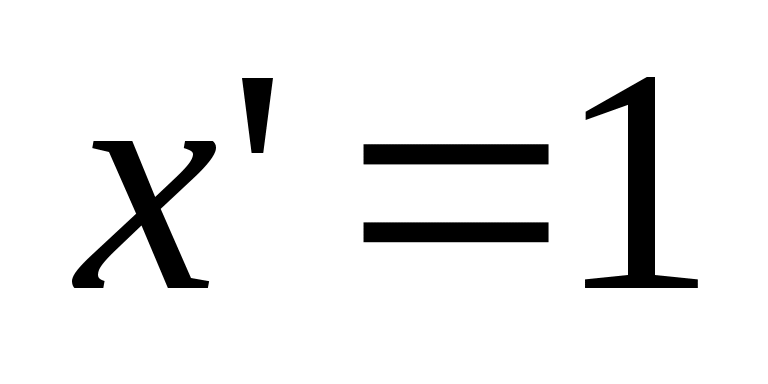 . .
Производная алгебраической суммы конечного числа дифференцируемых функций равна такой же сумме производных этих функций:
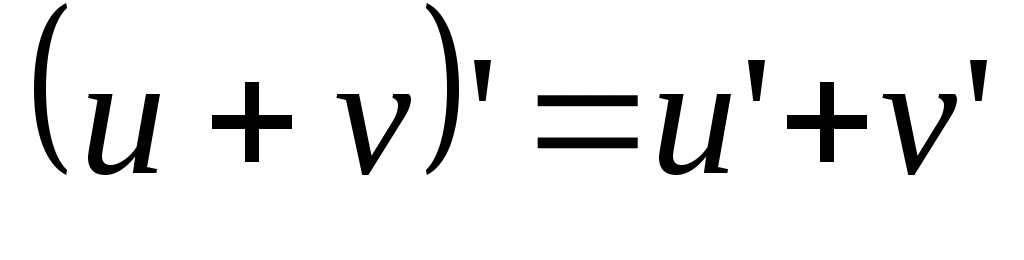 . .
Производная произведения двух дифференцируемых функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго:
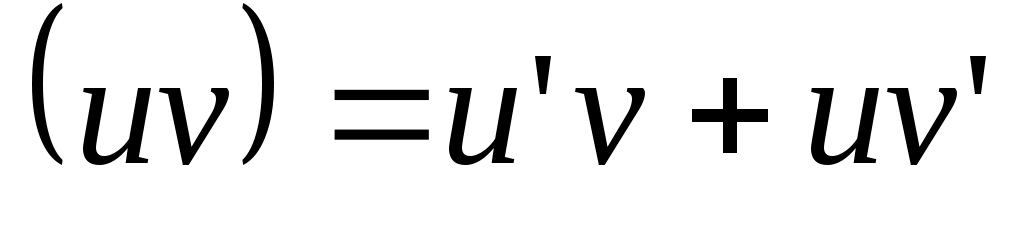 . .
Производная частного двух дифференцируемых функций находится по формуле:
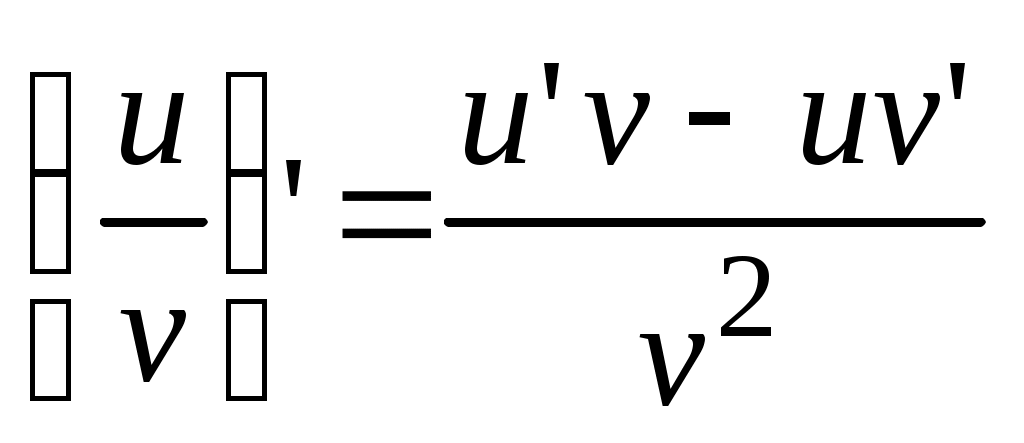 , (если , (если 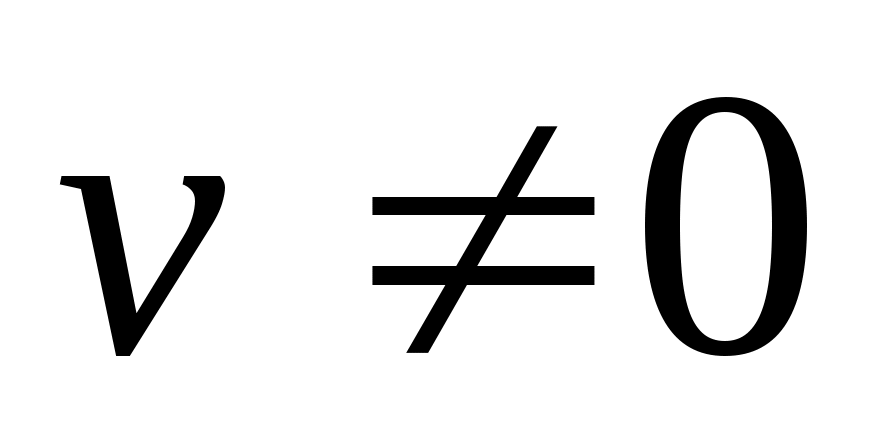 ). ).
Постоянный множитель можно выносить за знак производной:
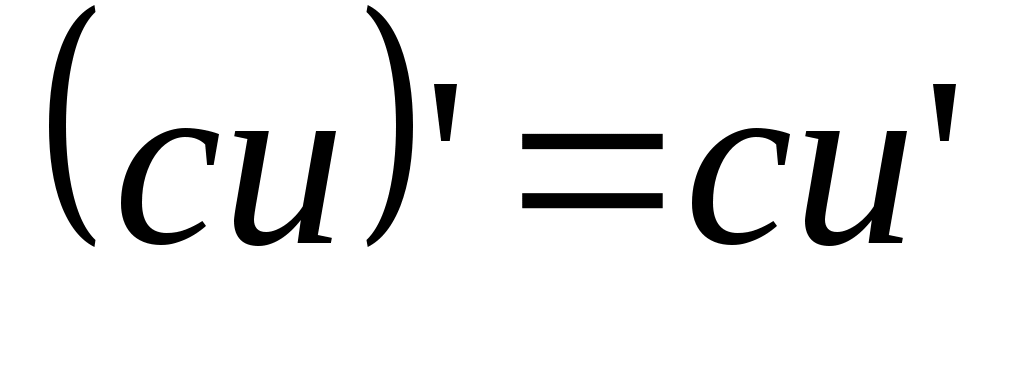 . .
Таблица производных элементарных функций.
1. 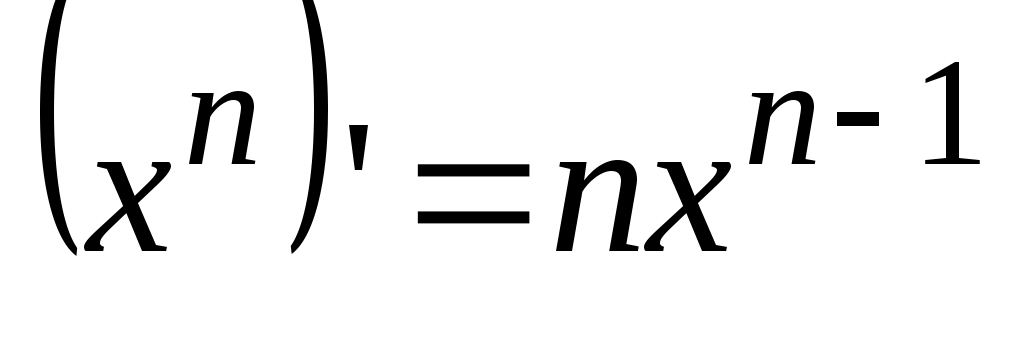 . .
|
6. 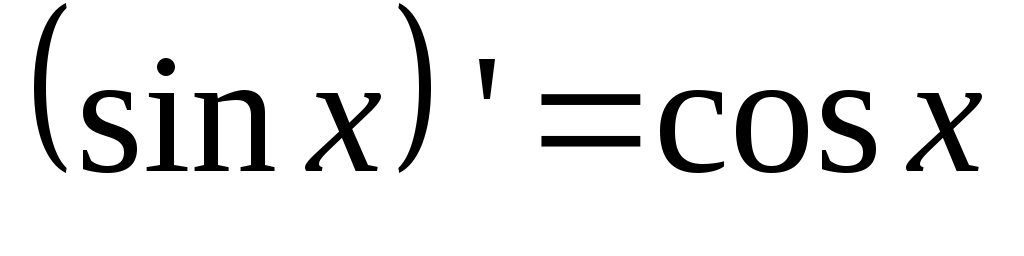 . .
|
11. 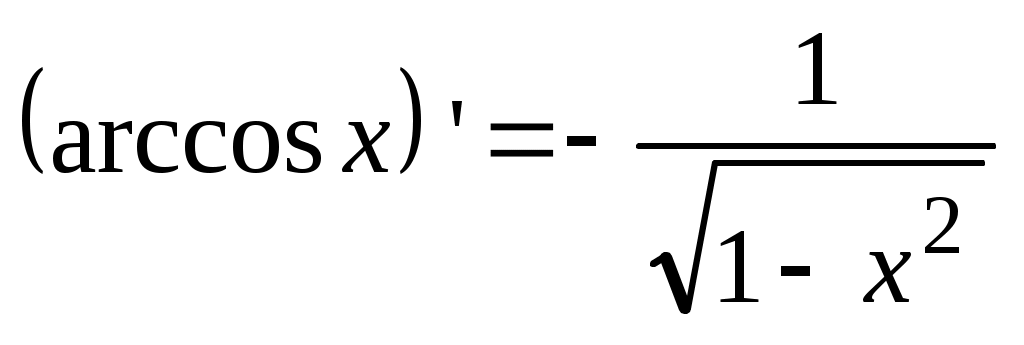 . .
|
2. 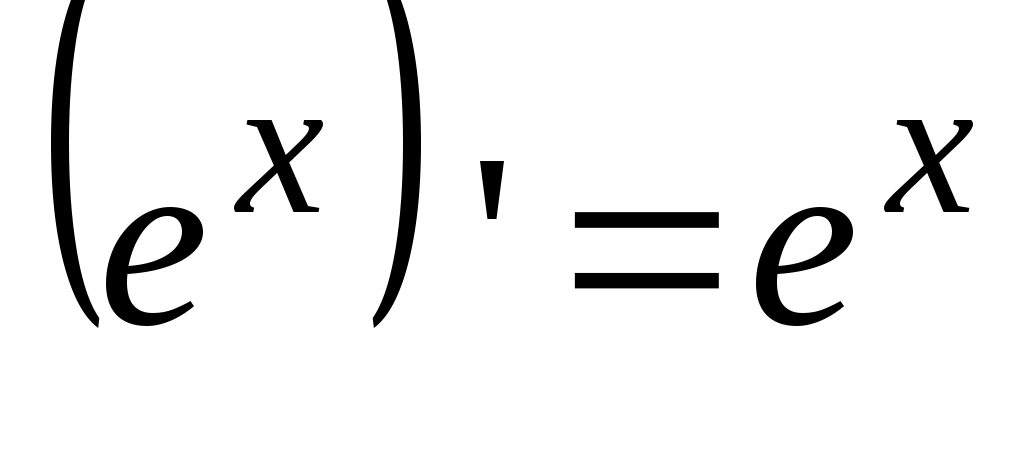 . .
|
7. 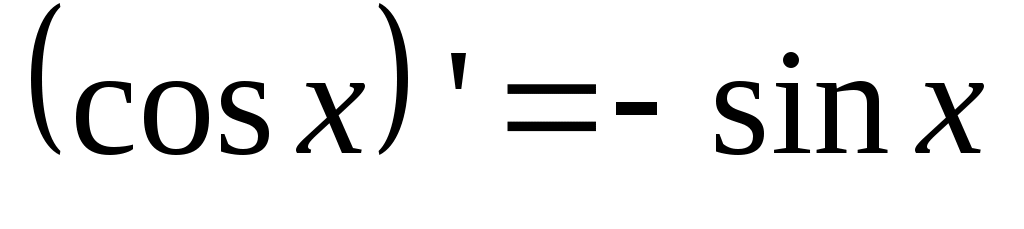 . .
|
12. 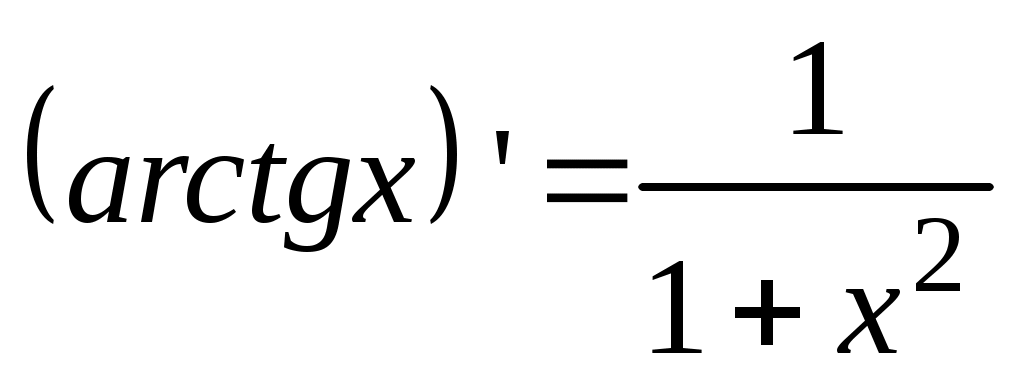 . .
|
3. 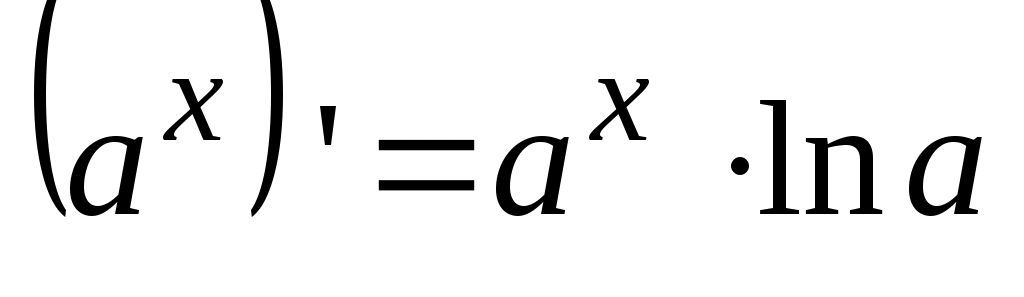 . .
|
8. 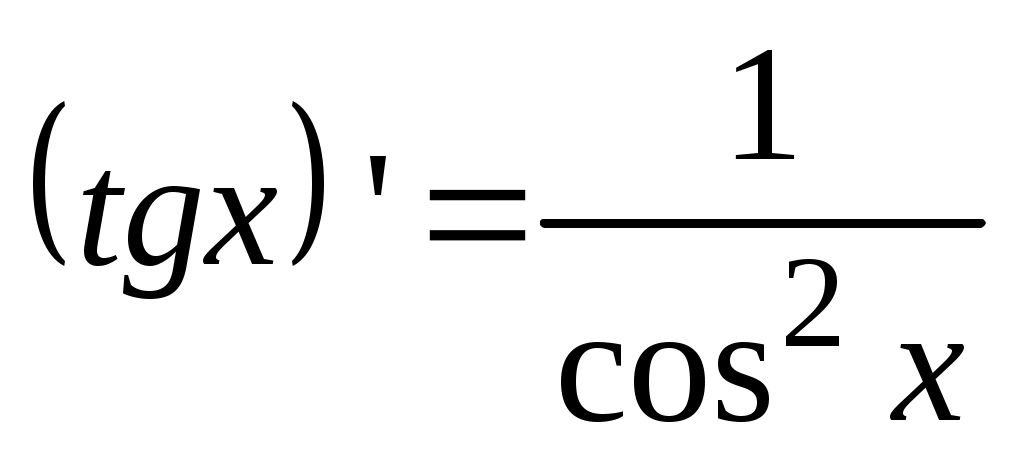 . .
|
13. 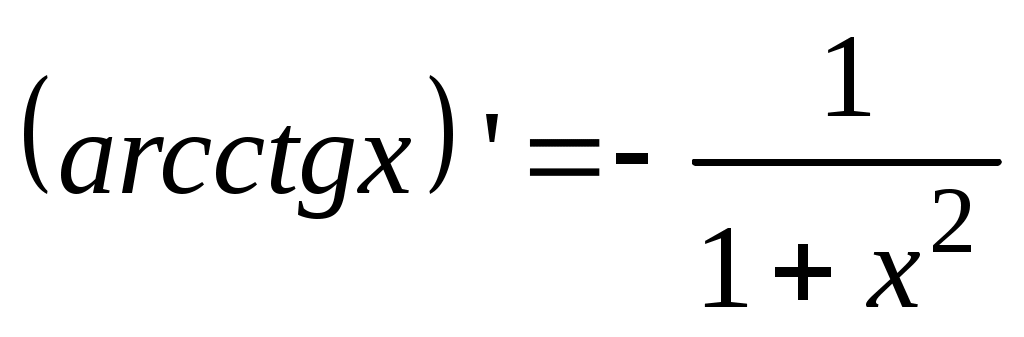
|
4. 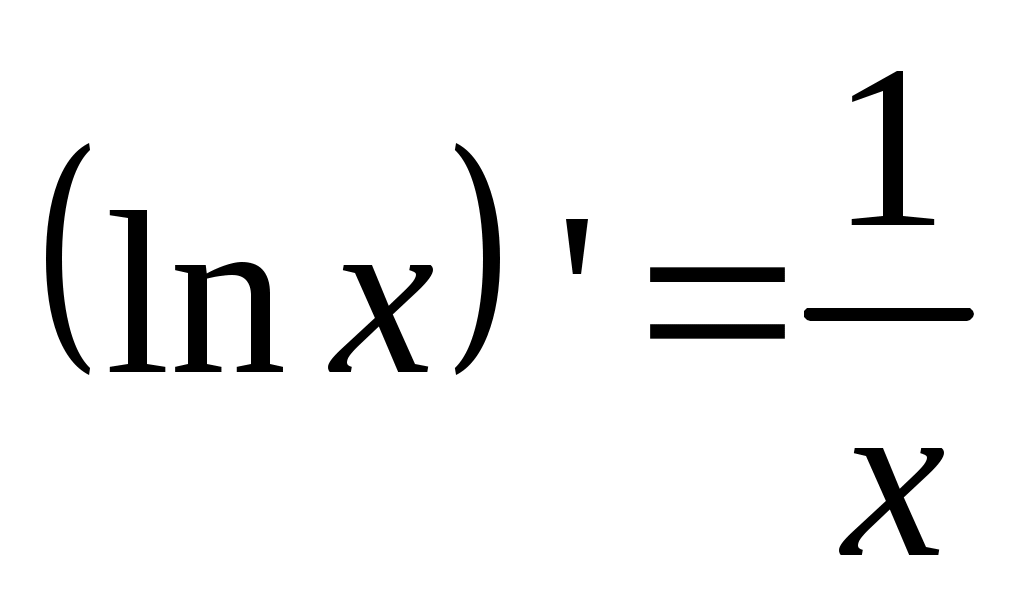 . .
|
9. 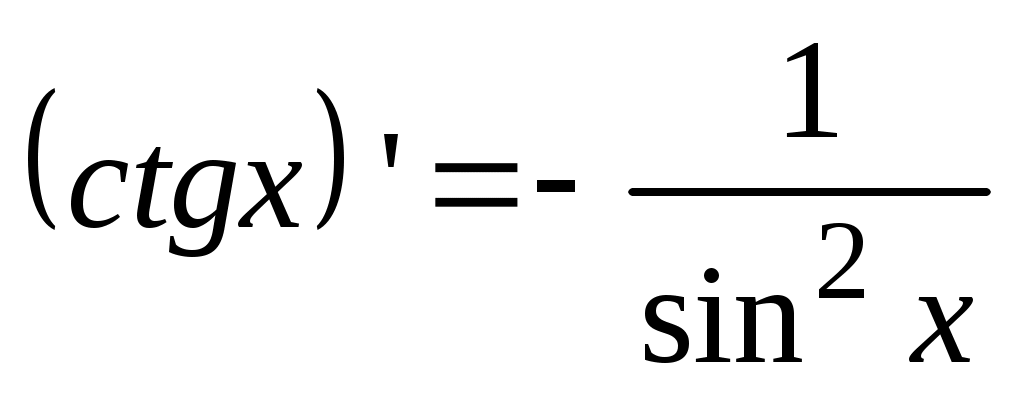 . .
|
|
5. 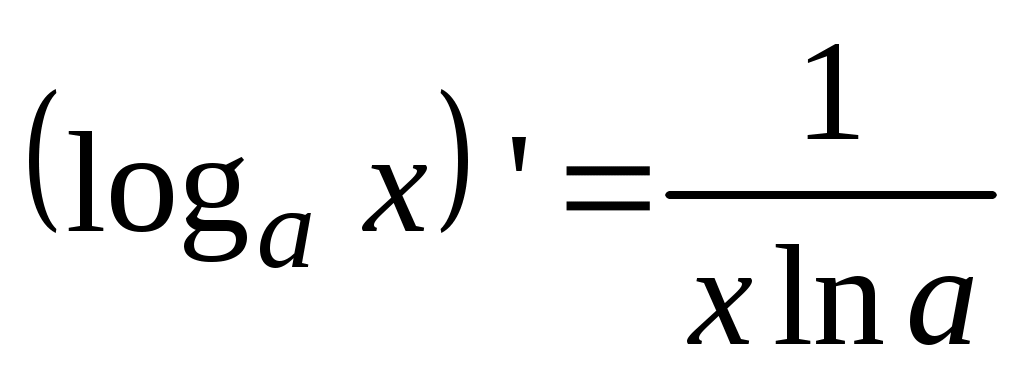 . .
|
10. 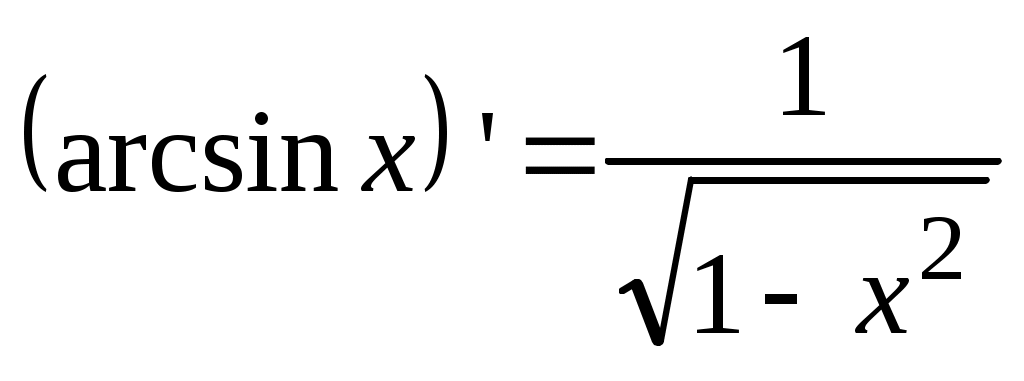 . .
|
|
Производные сложной и обратной функции.
Пусть 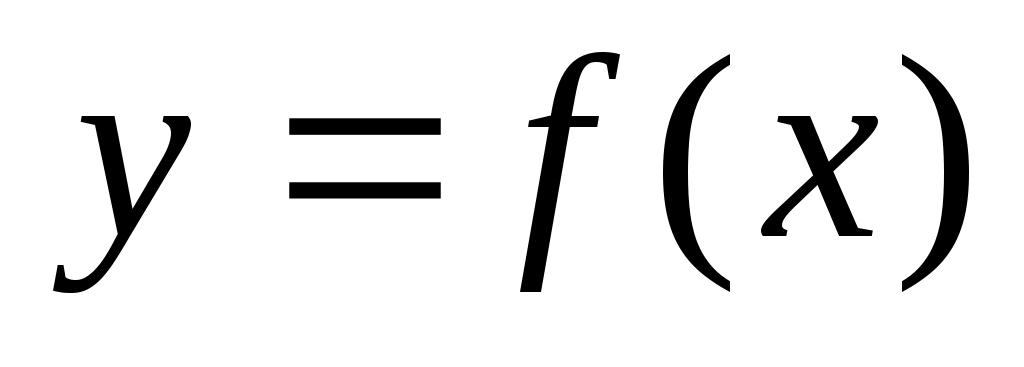 есть функция от независимой переменной есть функция от независимой переменной 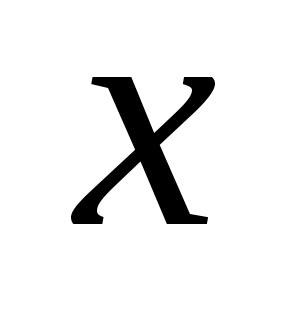 , определенной на промежутке , определенной на промежутке  с областью значений с областью значений 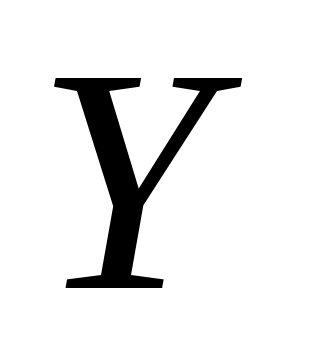 . Поставим в соответствие каждому . Поставим в соответствие каждому 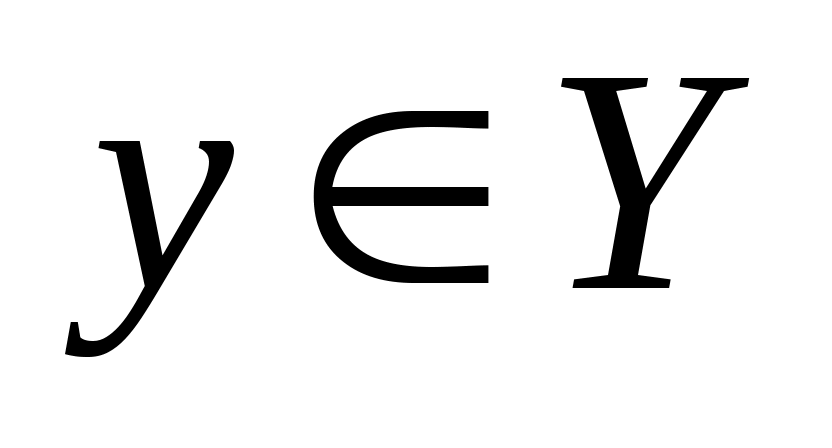 единственное значение единственное значение 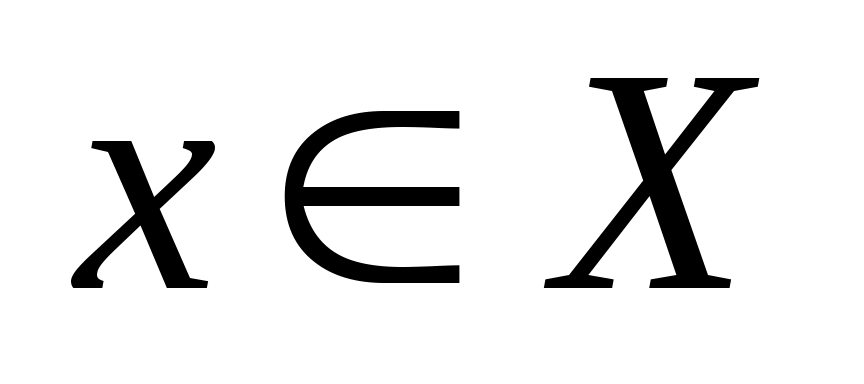 , при котором , при котором 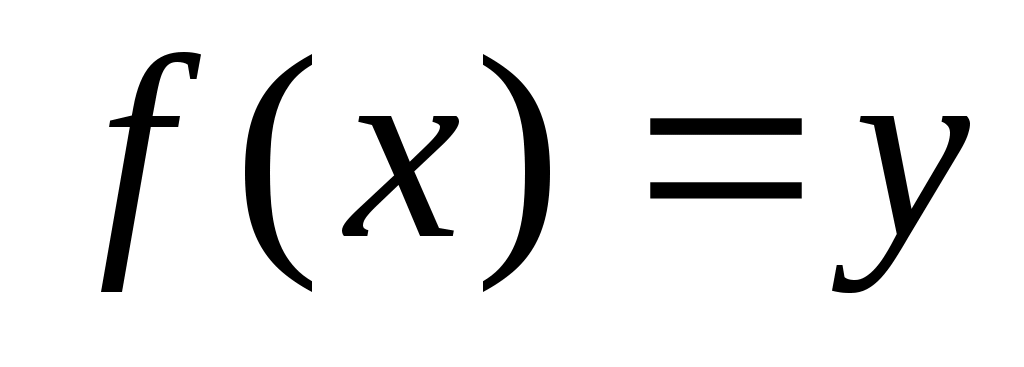 . Тогда полученная функция . Тогда полученная функция 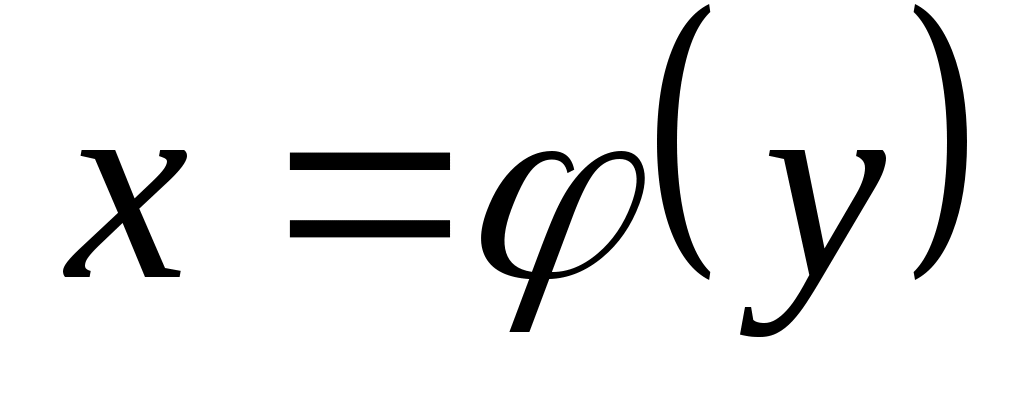 , определенная на промежутке , определенная на промежутке 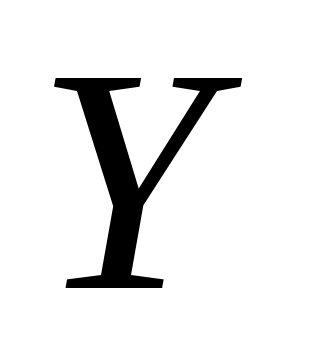 с областью значений с областью значений  , называется обратной. , называется обратной.
Дифференцирование обратной функции. Для дифференцируемой функции с производной, не равной нулю, производная обратной функции равна обратной величине производной данной функции, т.е.
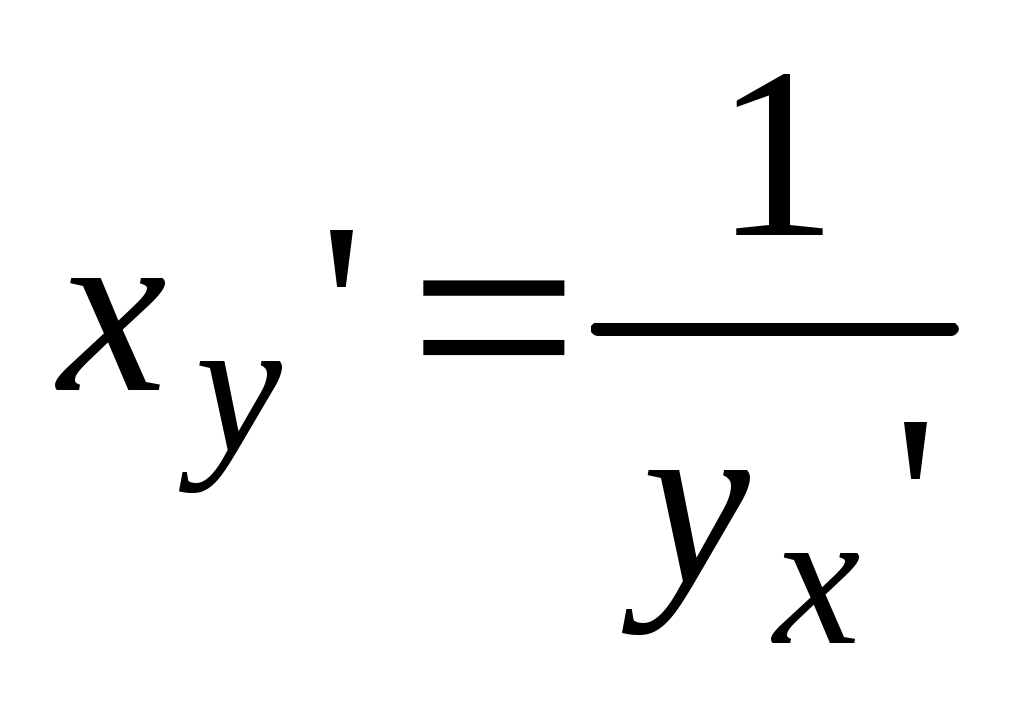 . .
Пусть функция 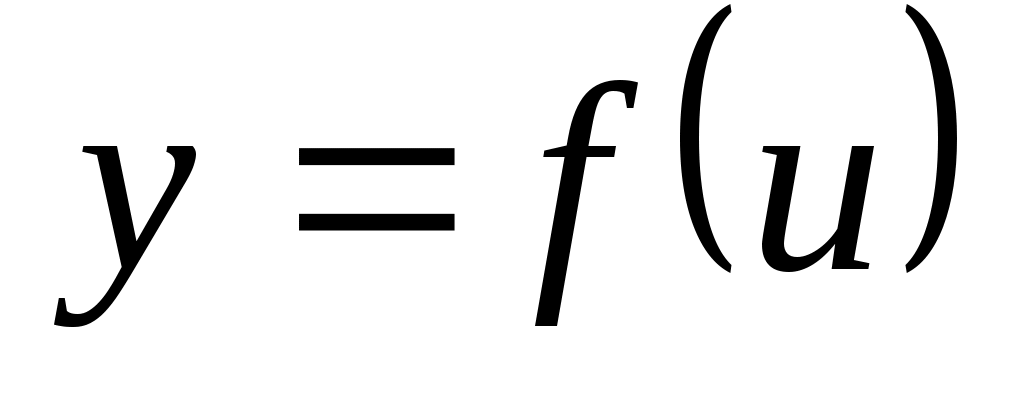 есть функция от переменной есть функция от переменной  , определенной на множестве , определенной на множестве 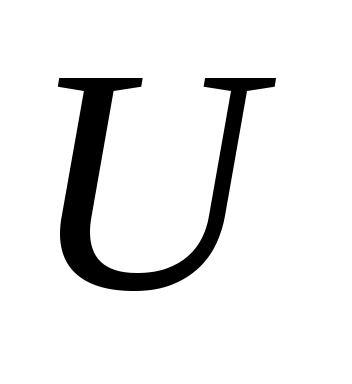 с областью значений с областью значений 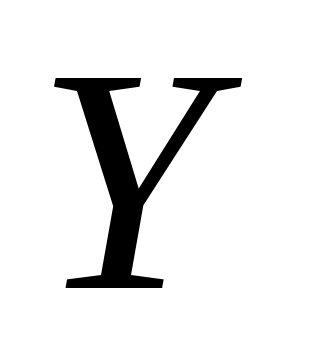 , а переменная , а переменная  в свою очередь является функцией в свою очередь является функцией 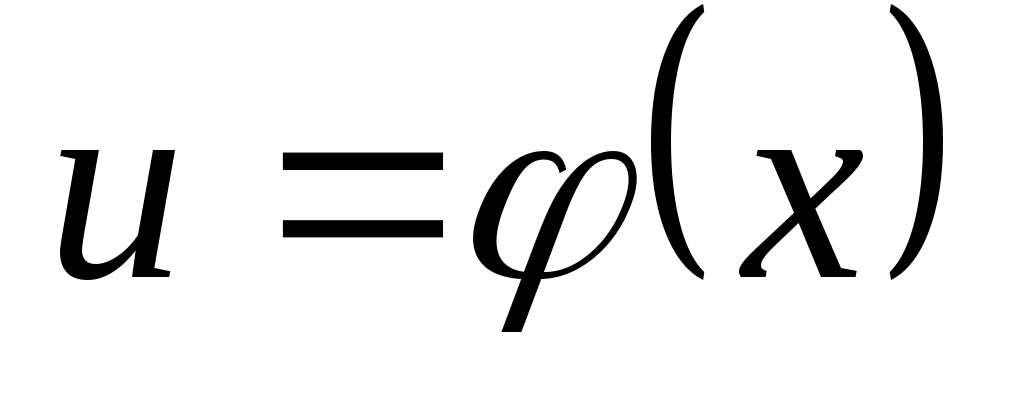 от переменой от переменой 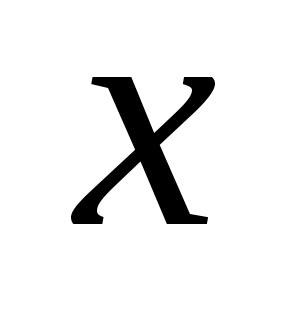 , определенной на множестве , определенной на множестве  с областью значений с областью значений 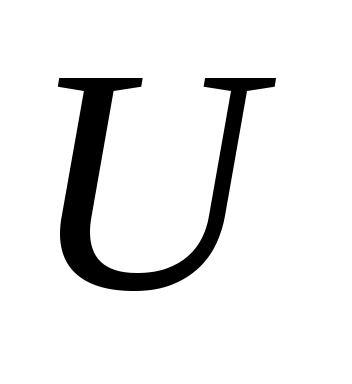 . Тогда заданная на множестве . Тогда заданная на множестве  функция функция 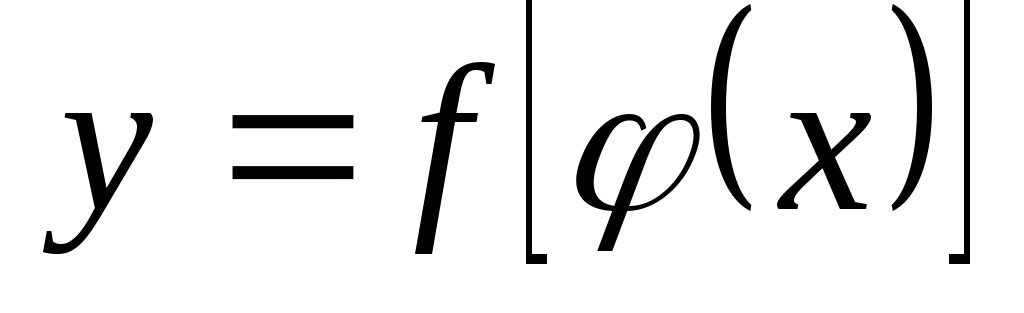 называется сложной функцией (или композицией функций, суперпозицией функций, функцией от функций). называется сложной функцией (или композицией функций, суперпозицией функций, функцией от функций).
Дифференцирование сложной функции. Если 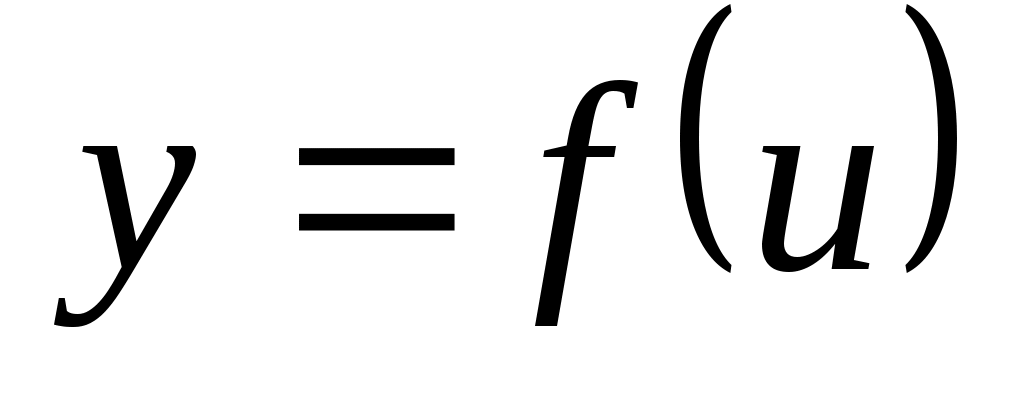 и и 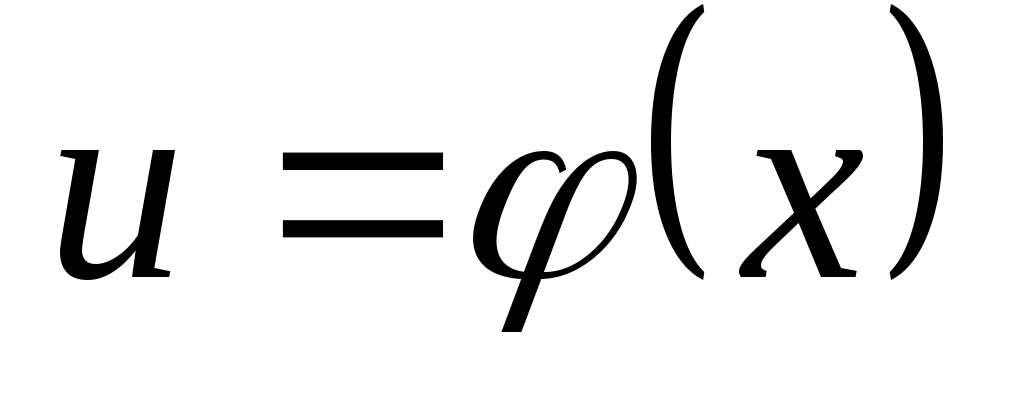 – дифференцируемые функции от своих аргументов, то производная сложной функции существует и равна производной данной функции по промежуточному аргументу и умноженной на производную самого промежуточного аргумента по независимой переменной – дифференцируемые функции от своих аргументов, то производная сложной функции существует и равна производной данной функции по промежуточному аргументу и умноженной на производную самого промежуточного аргумента по независимой переменной 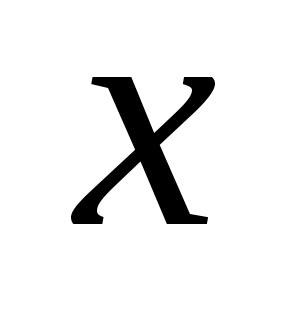 , т.е. , т.е.
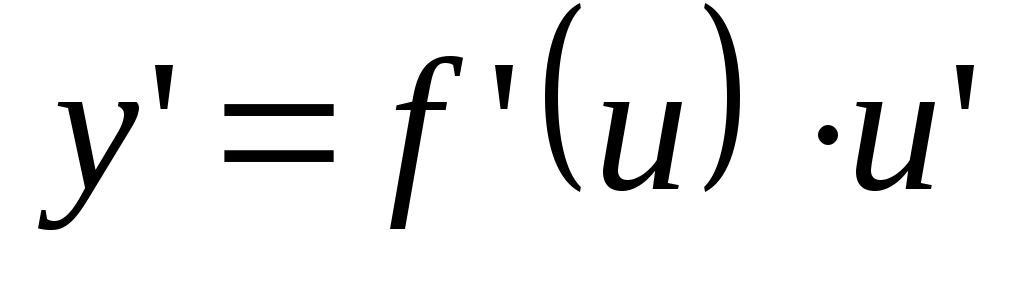 . .
Пример. Найти производные функций:
а)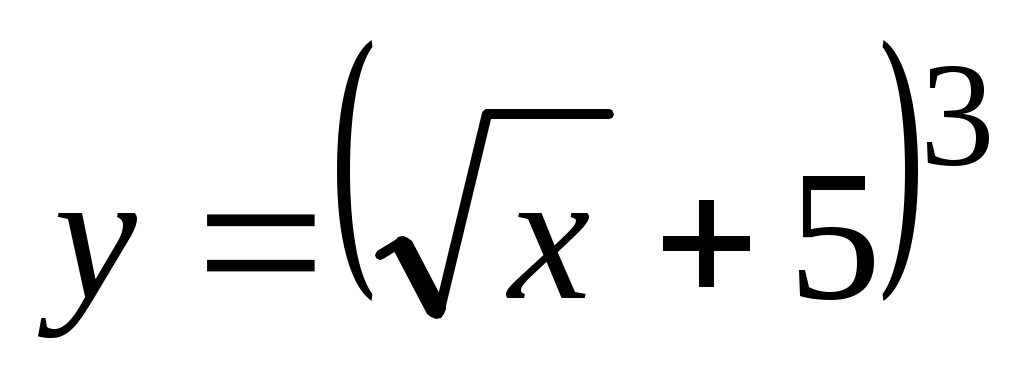 ; б) ; б)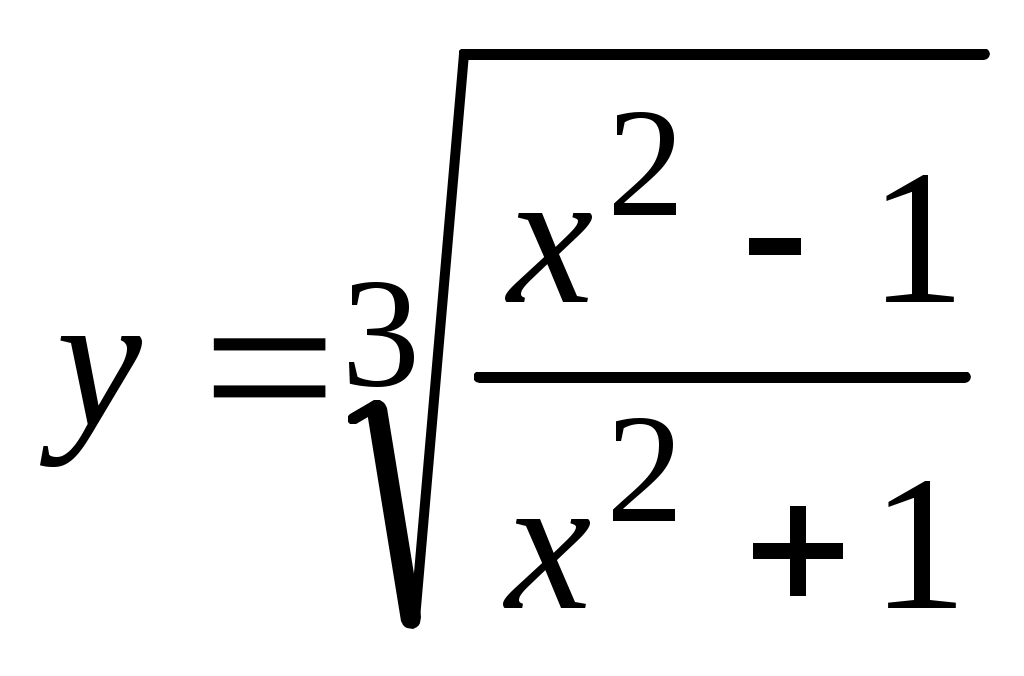 ; в) ; в)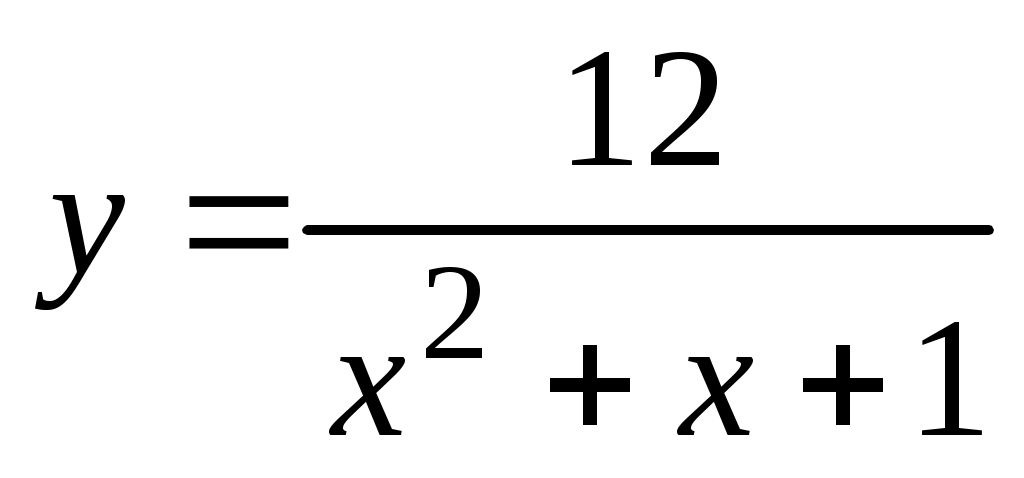 ; г) ; г)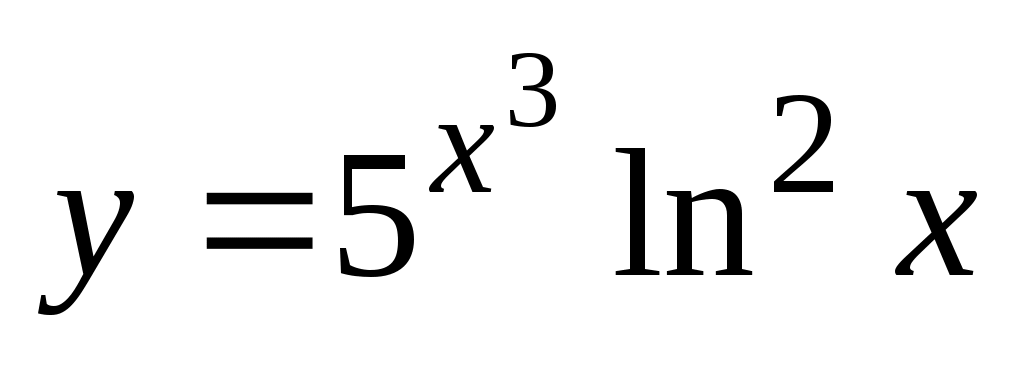 ; д) ; д)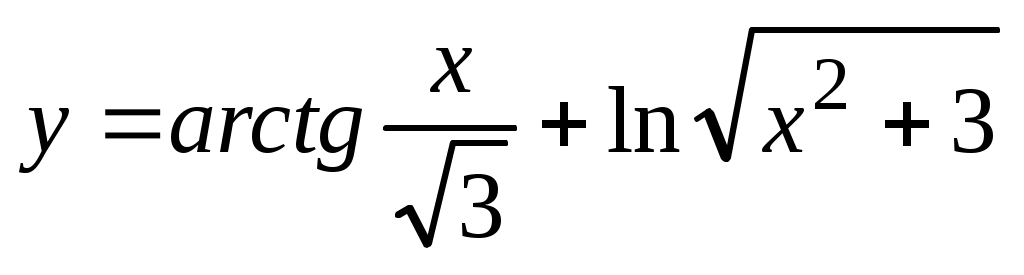
Решение. а) Функцию можно представить в виде 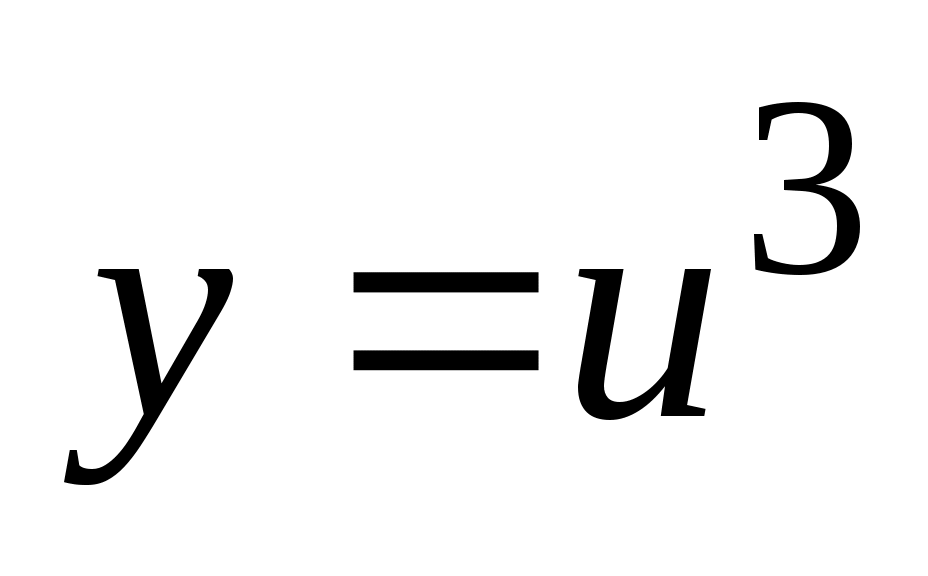 , где , где 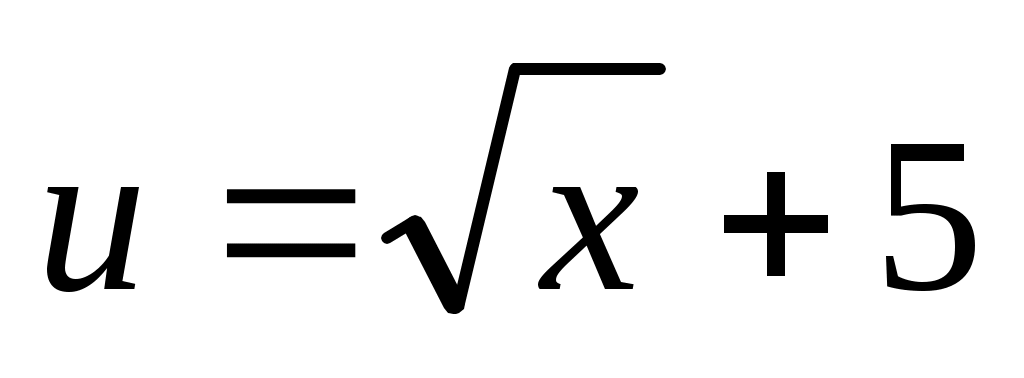 . Поэтому по формуле дифференцирования сложной функции . Поэтому по формуле дифференцирования сложной функции
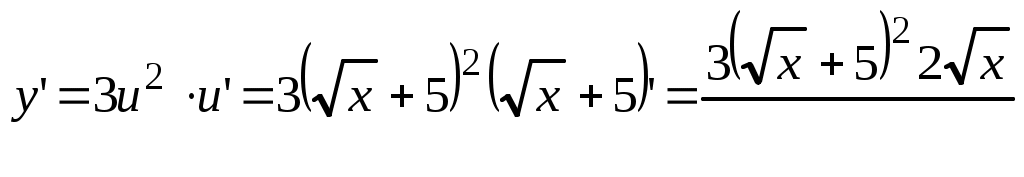 . .
б) Имеем 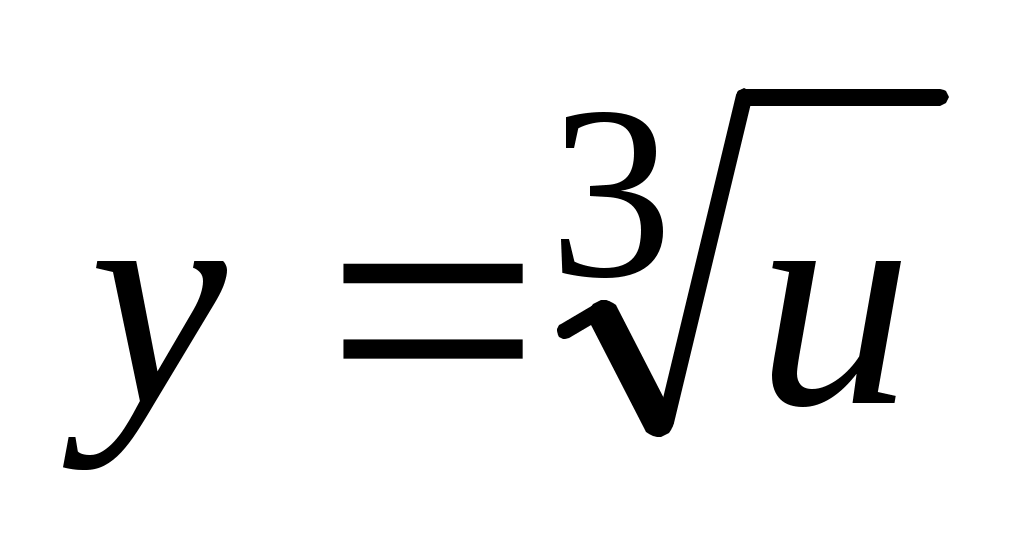 , где , где 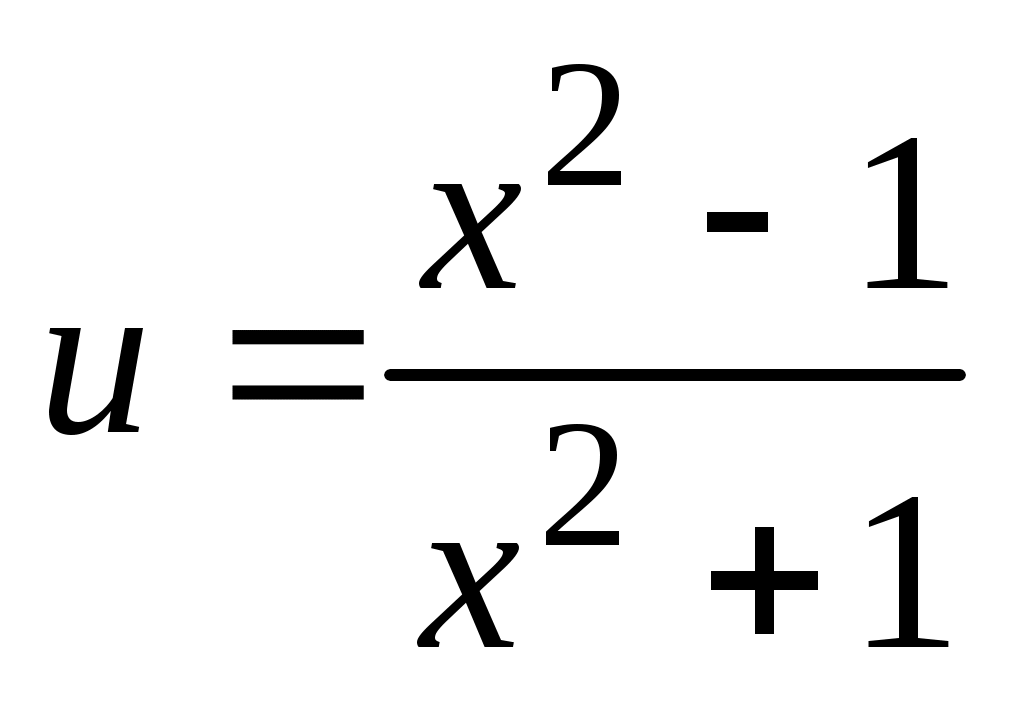 , поэтому получаем , поэтому получаем

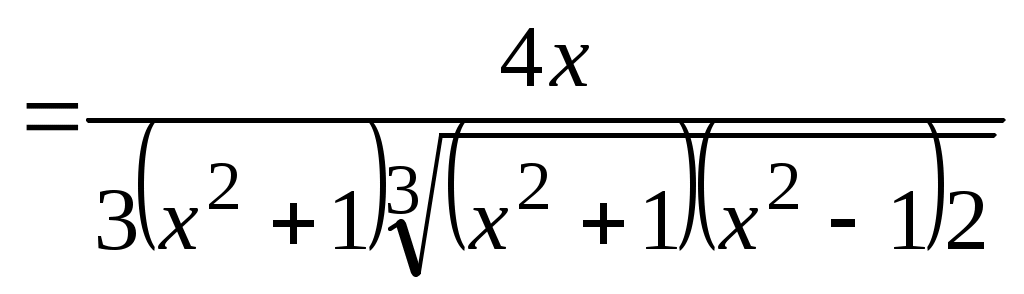 . .
в) Вынося постоянный множитель 12 за знак производной, получим
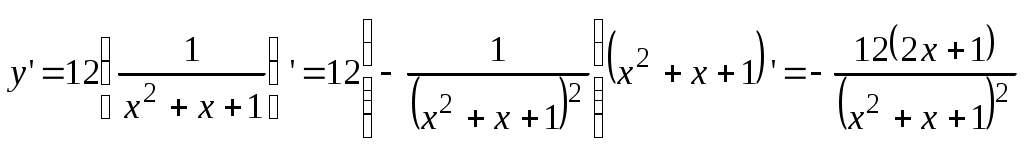 . .
г) Данная функция представляет произведение двух функций  и и 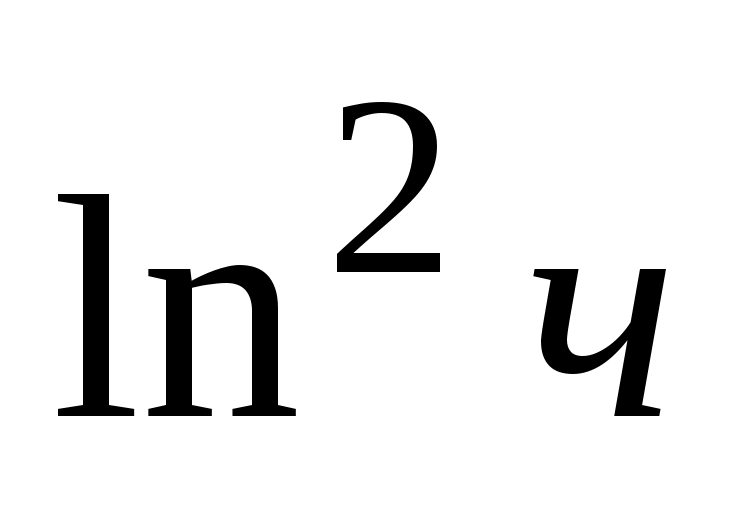 , каждая из которых является сложной функцией ( , каждая из которых является сложной функцией (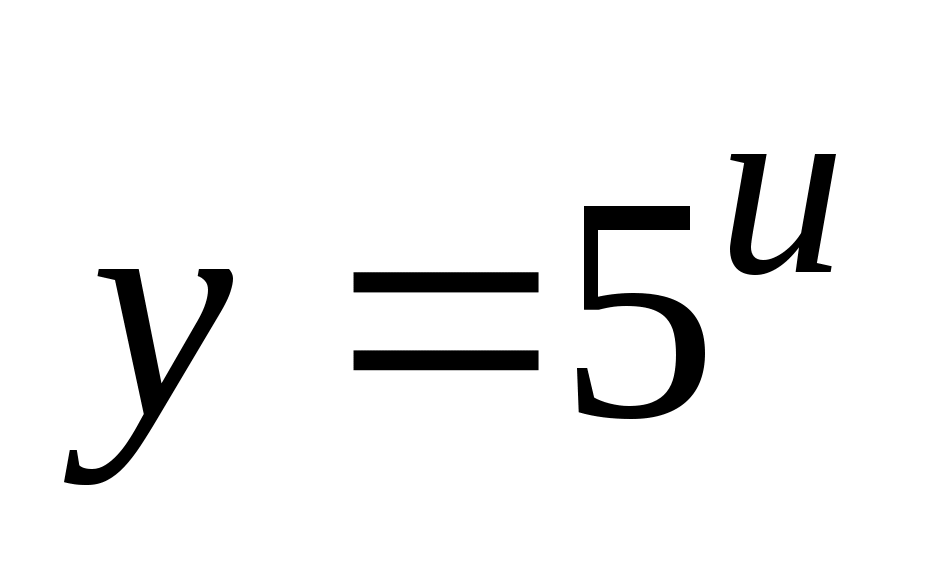 , где , где 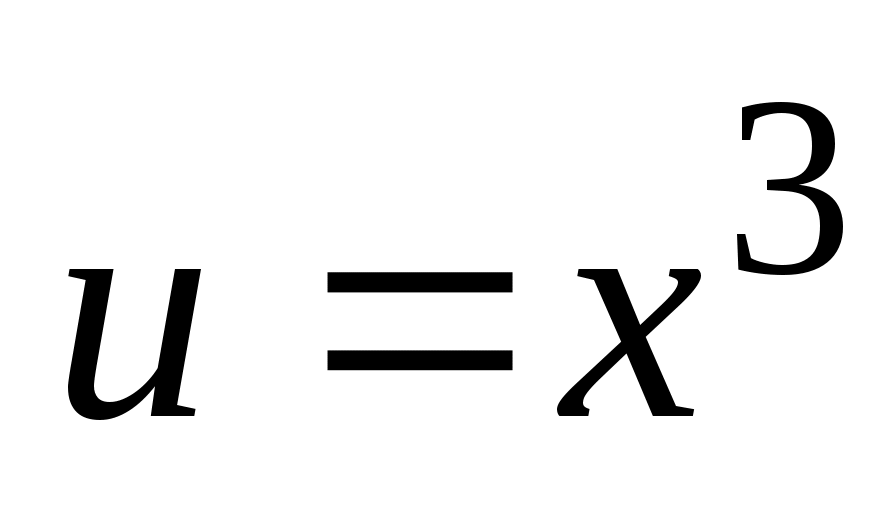 ; ; 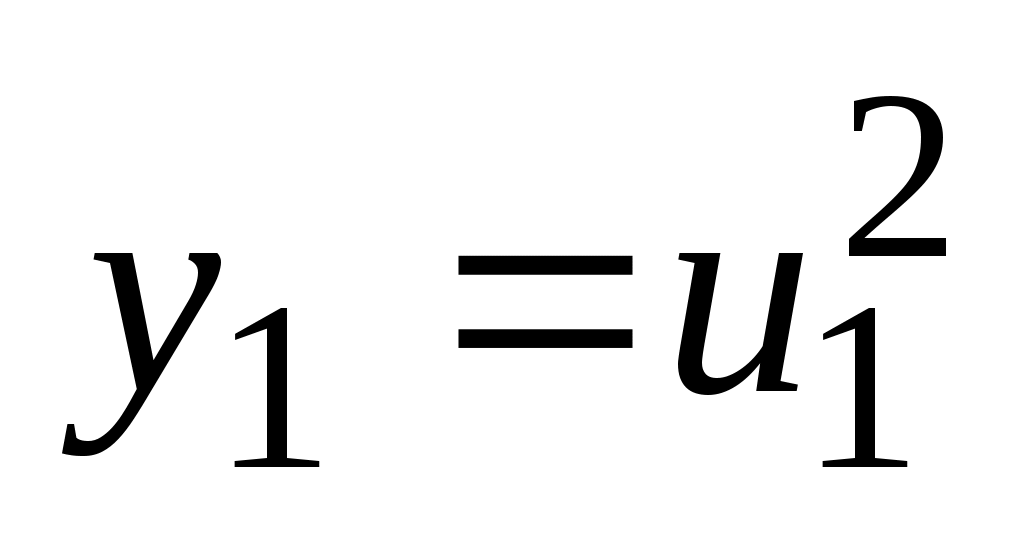 , где , где 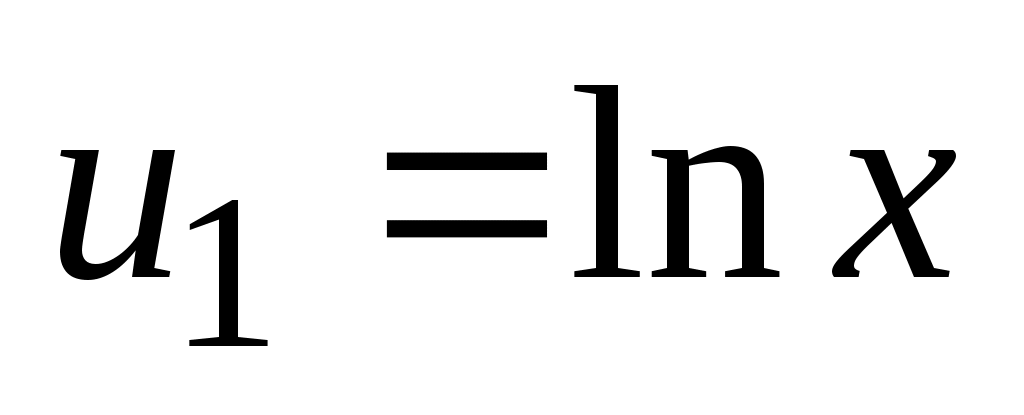 ). Поэтому ). Поэтому
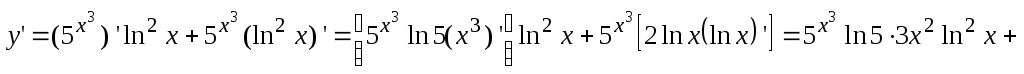
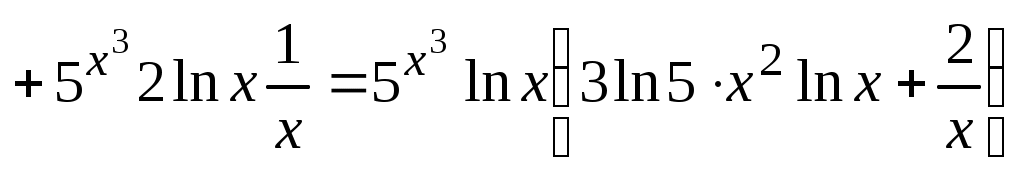 . .
д) Представим функцию в виде 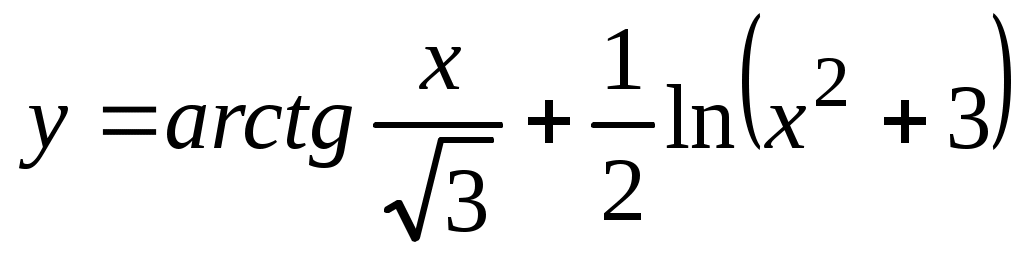 . Теперь . Теперь
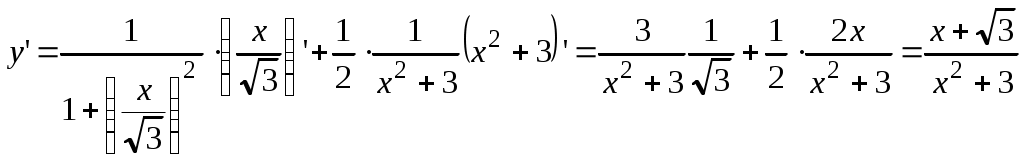 . .
ИНТЕГРИРОВАНИЕ.
Функция 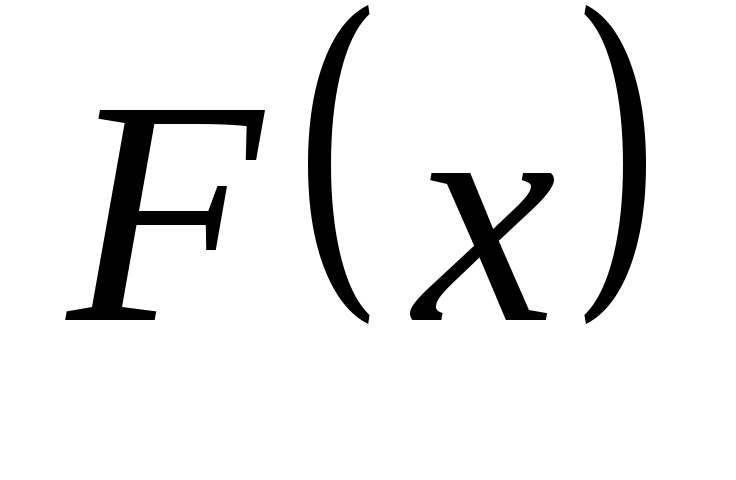 называется первообразной функцией для функции называется первообразной функцией для функции 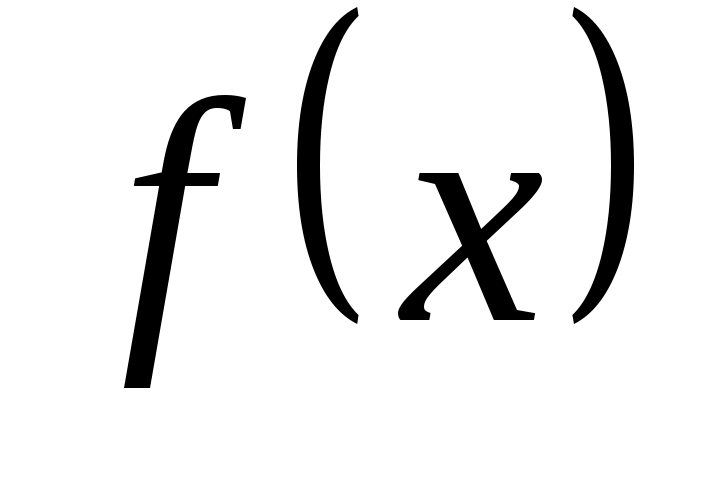 на промежутке на промежутке  , если в каждой точке , если в каждой точке 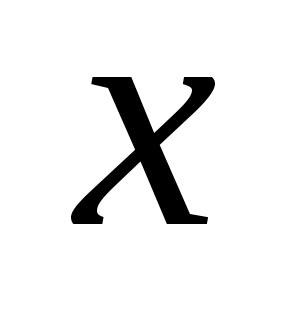 этого промежутка этого промежутка 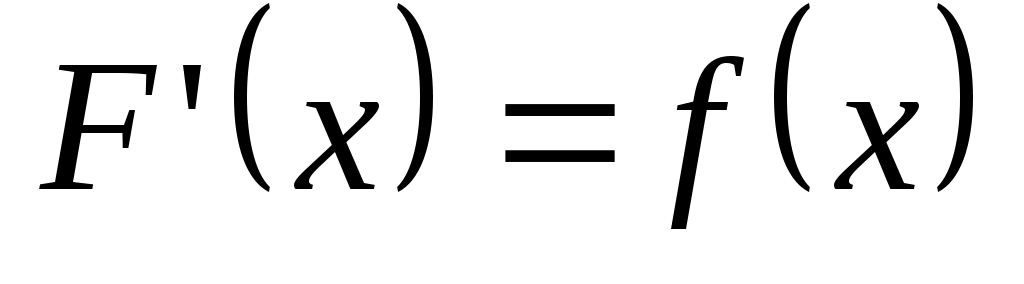 . .
Совокупность всех первообразных для функции 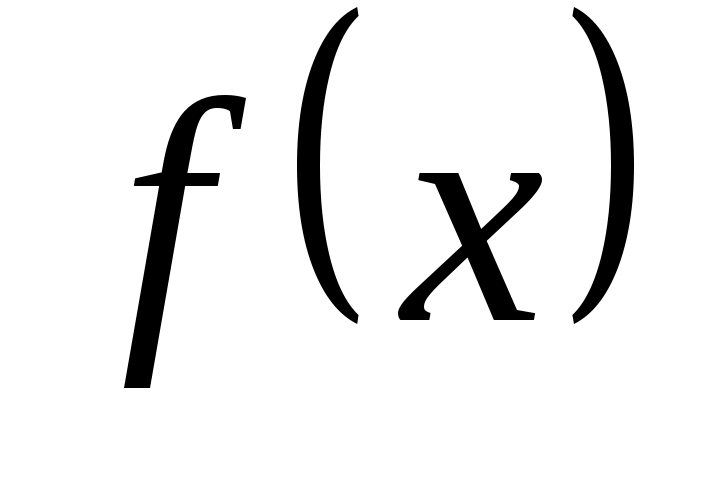 на промежутке на промежутке  называется неопределенным интегралом от функции называется неопределенным интегралом от функции 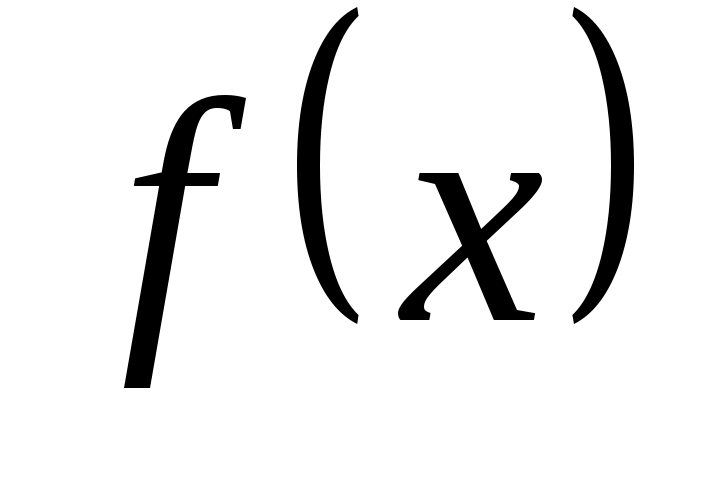 и обозначается и обозначается 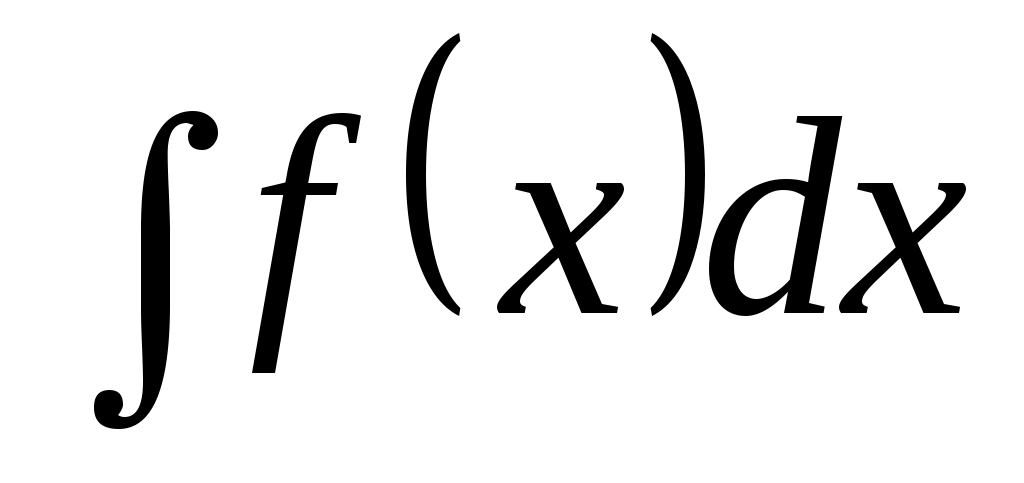 , где , где 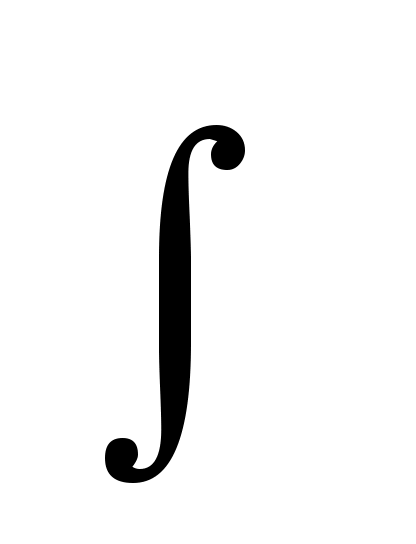 – знак интеграла, – знак интеграла, 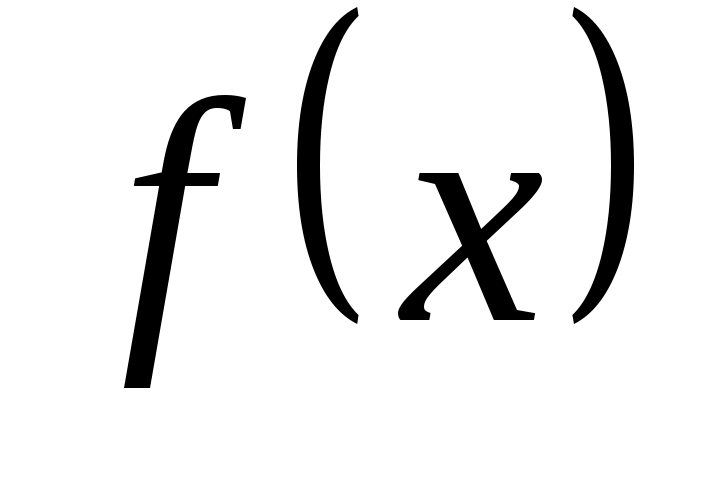 – подынтегральная функция, – подынтегральная функция, 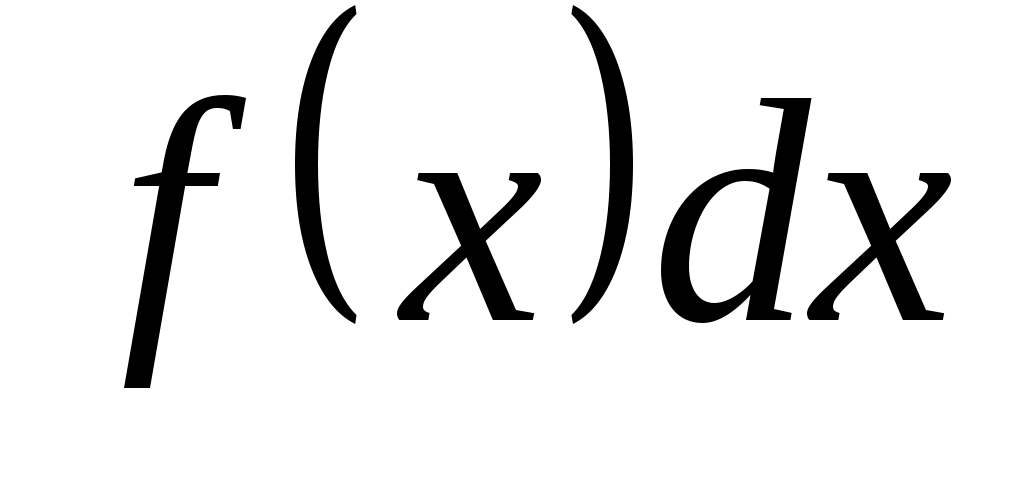 – подынтегральное выражение. Таким образом, – подынтегральное выражение. Таким образом,
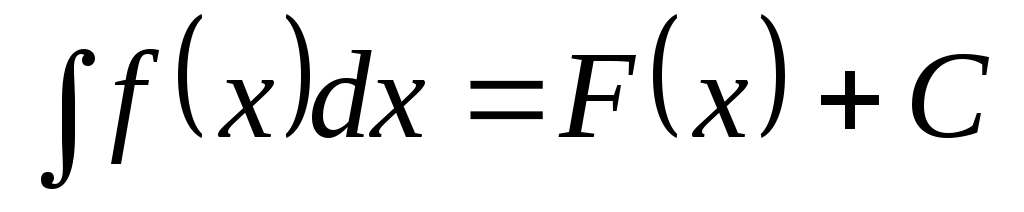 , ,
где 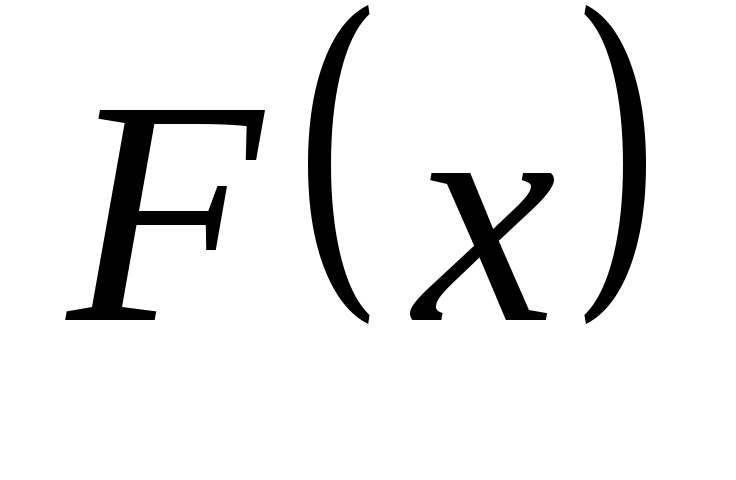 – некоторая первообразная для – некоторая первообразная для 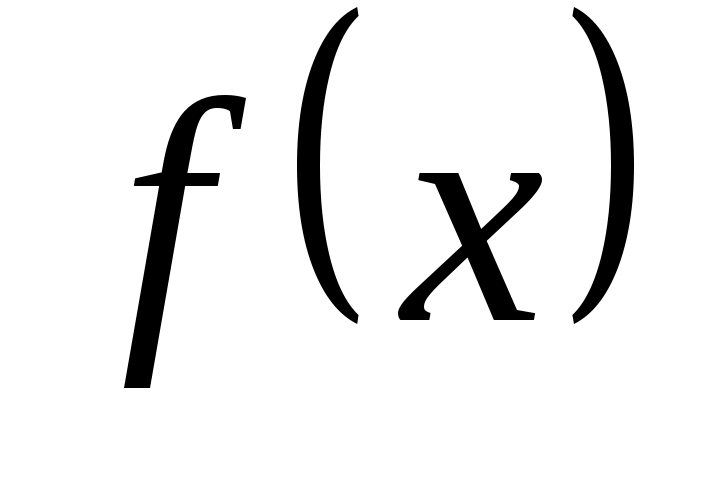 , С – произвольная постоянная. , С – произвольная постоянная.
Свойства неопределенного интеграла.
Производная от неопределенного интеграла равна подынтегральной функции:
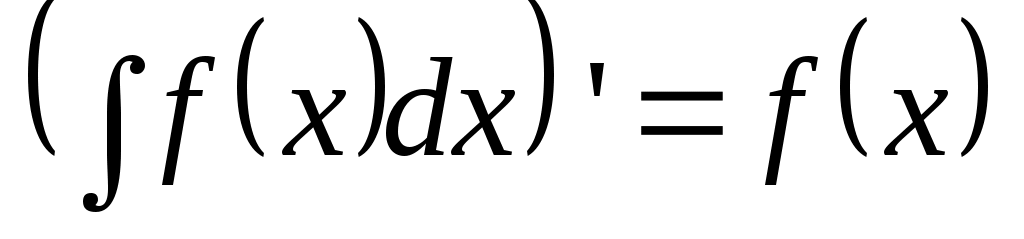 . .
Дифференциал неопределенного интеграла равен подынтегральному выражению:
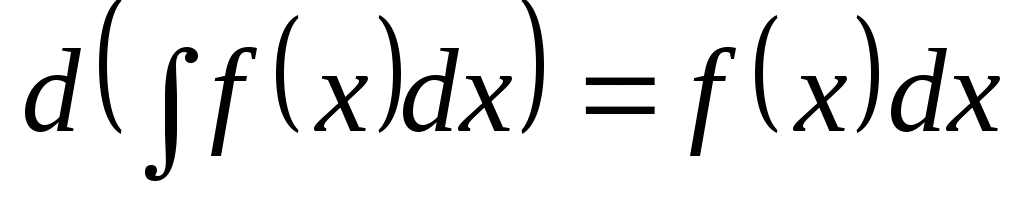 . .
Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого, т.е.
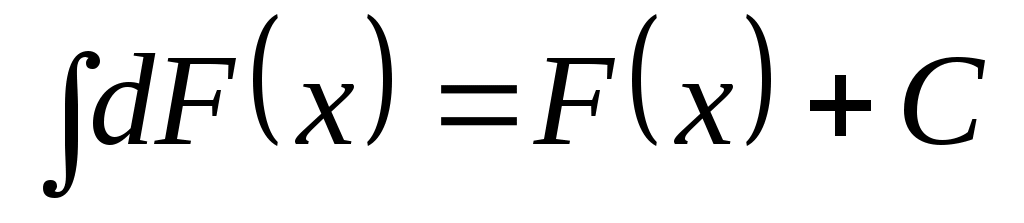 . .
Постоянный множитель можно выносить за знак интеграла:
 . .
Интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов от этих функций:
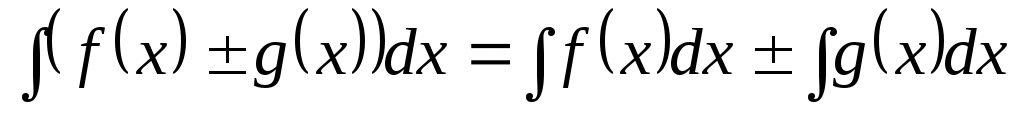 . .
Таблица интегралов от элементарных функций.
1. 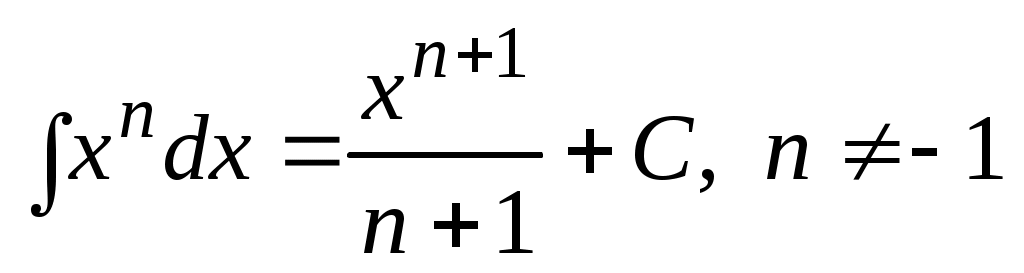
|
2. 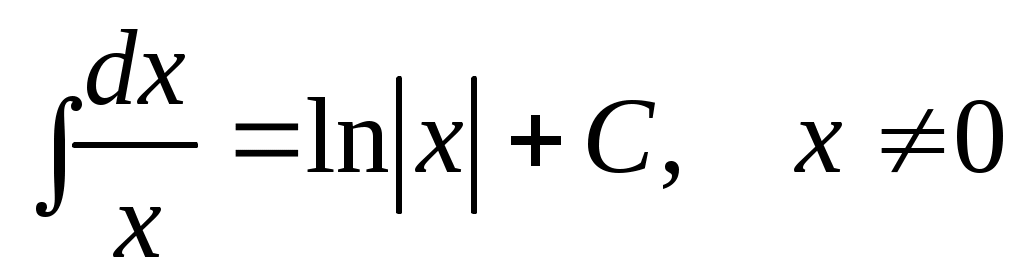
|
3. 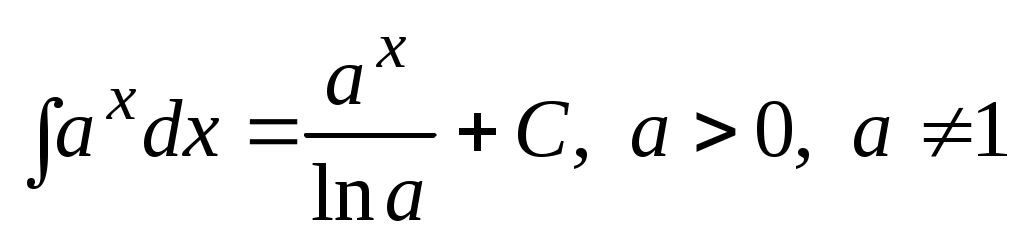
|
4. 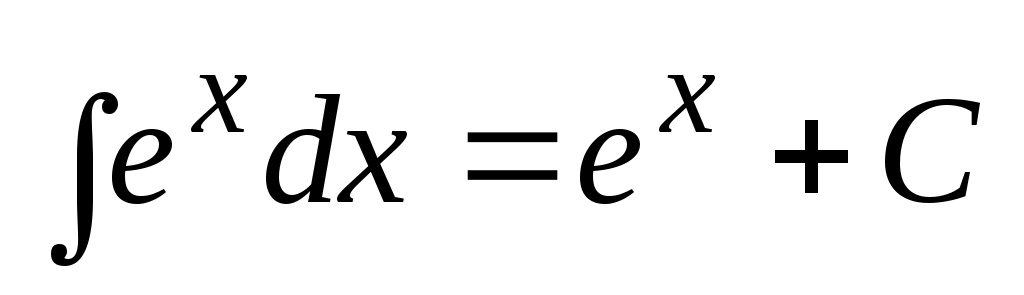
|
5. 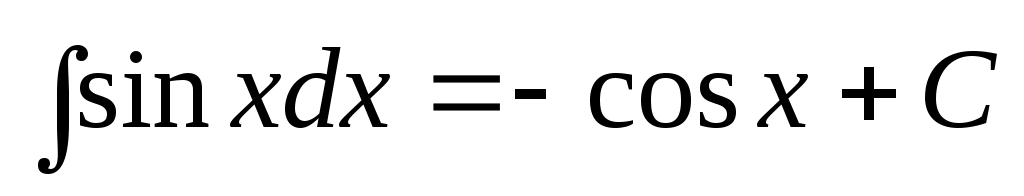
|
6. 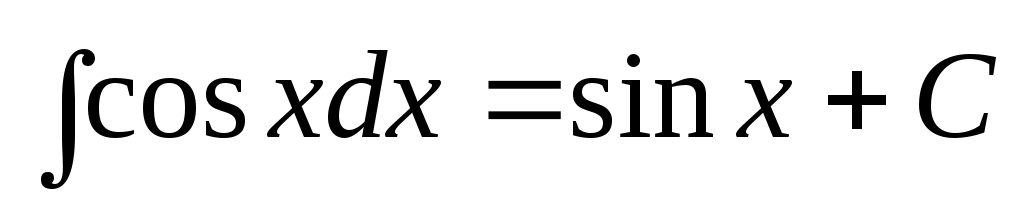
|
7. 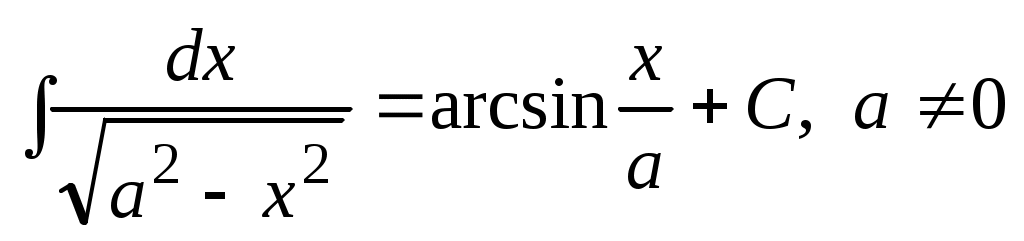
|
8. 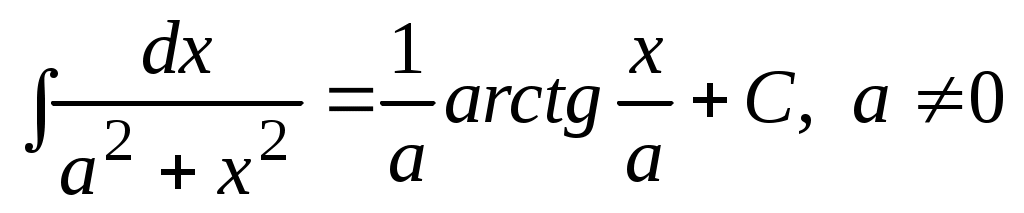
|
9. 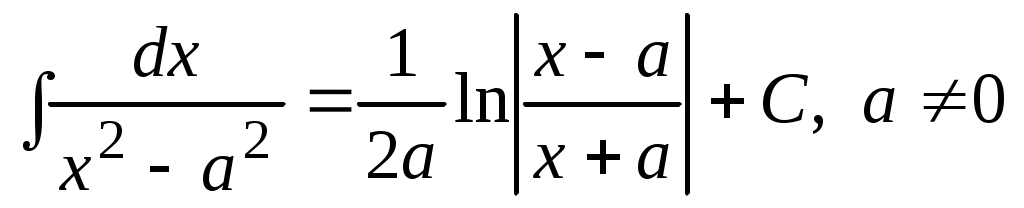
|
10. 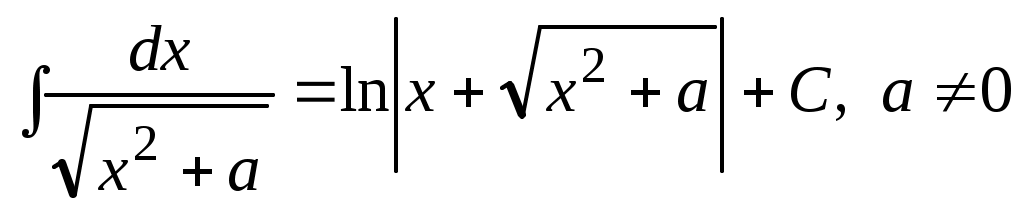
| |
|
|
 Скачать 1.53 Mb.
Скачать 1.53 Mb.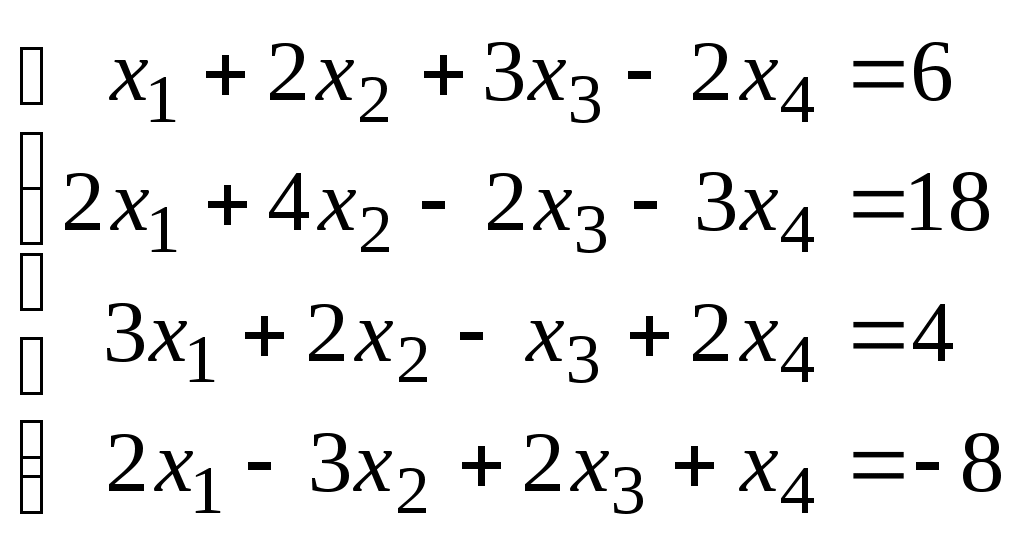 .
.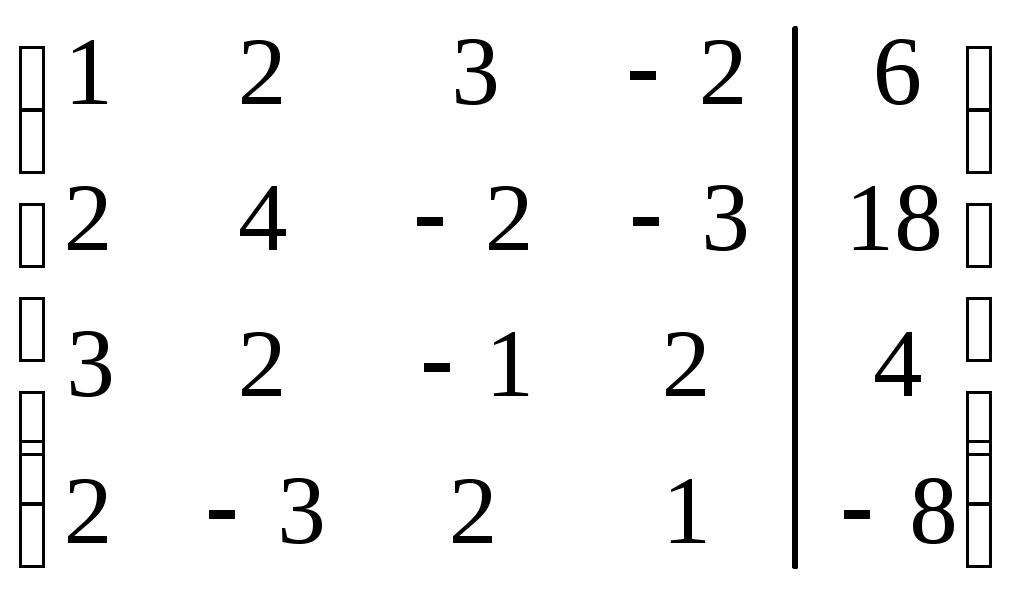 .
.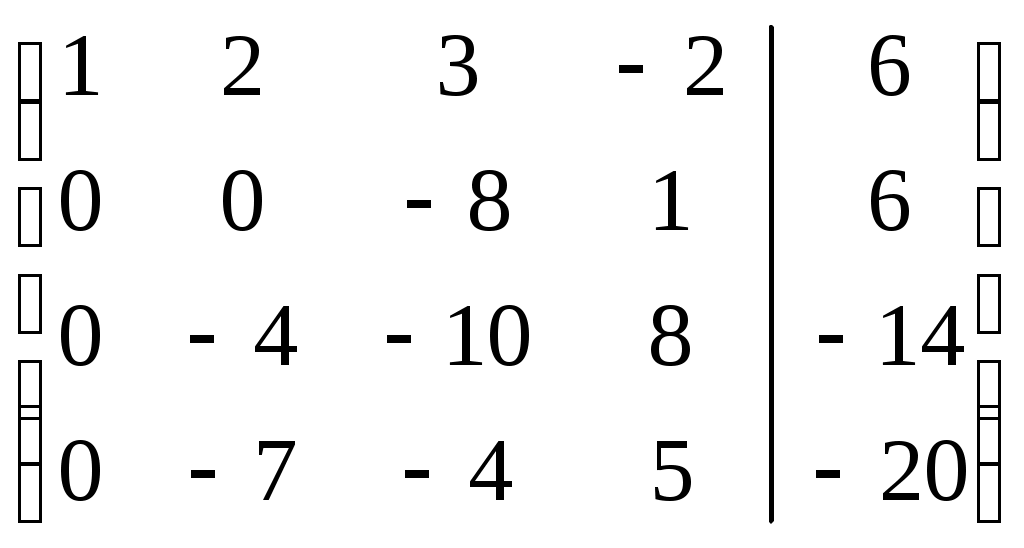
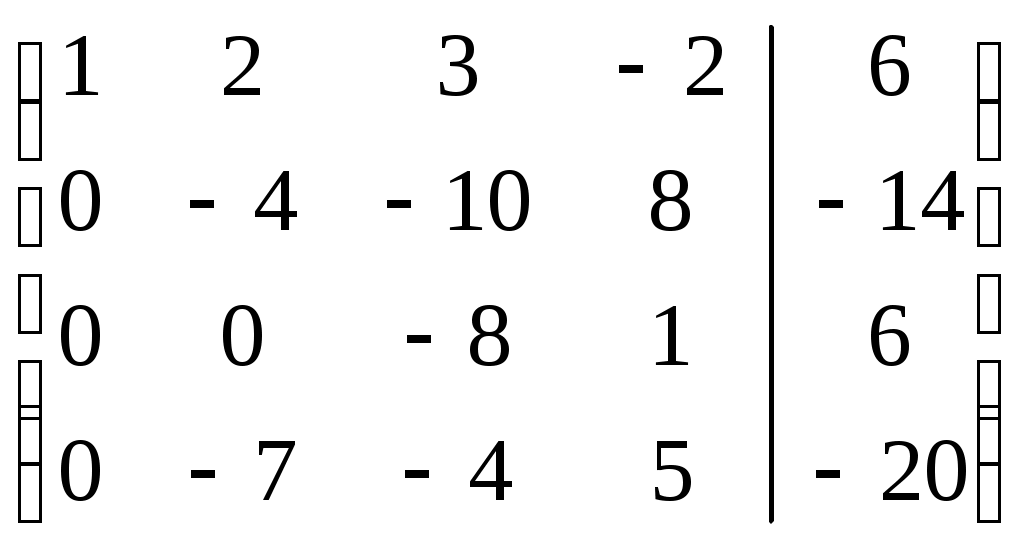 .
.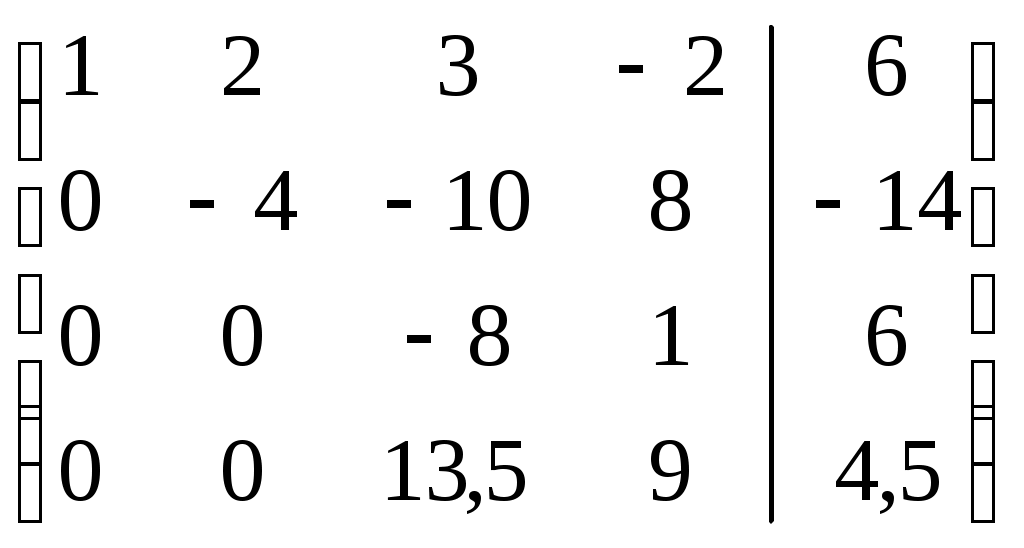
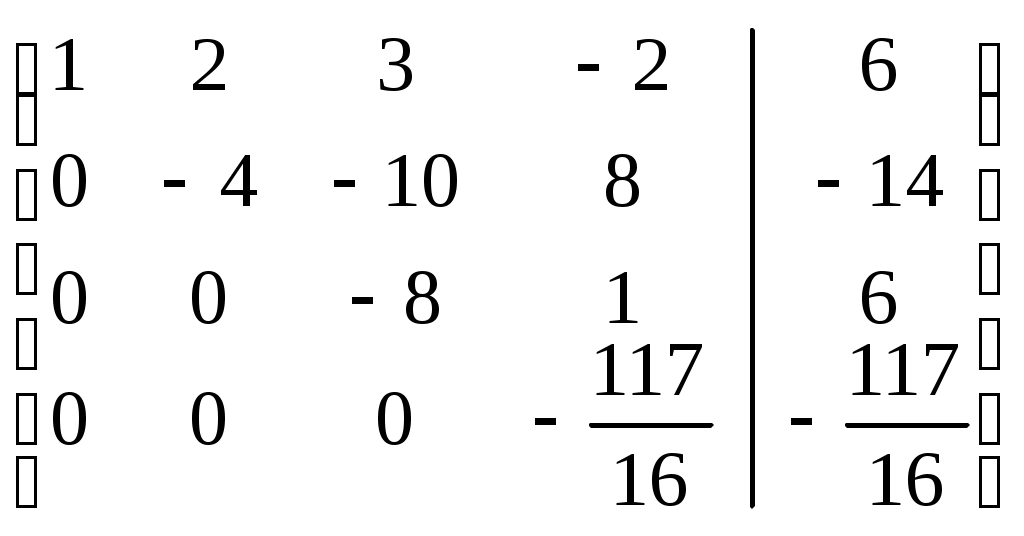 .
.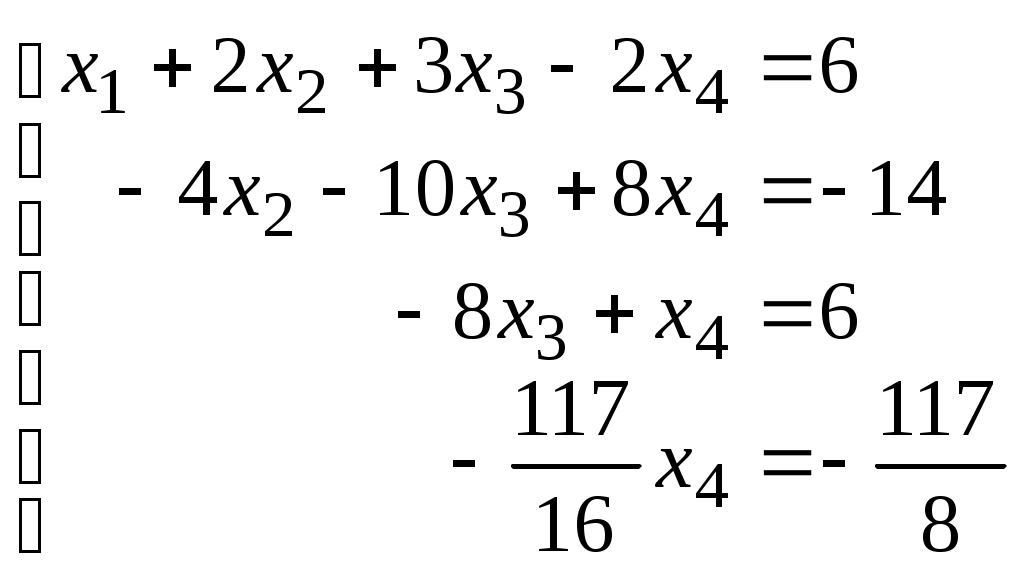 ,
,
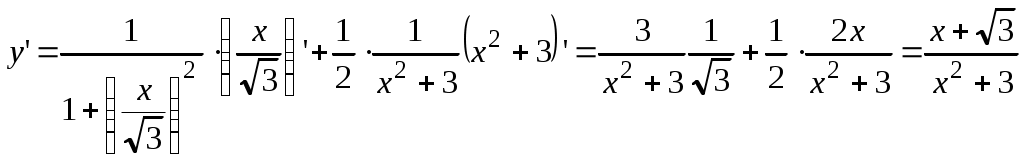 .
.