Матем. КР1 для психологов. Матрицы. Операции над матрицами
 Скачать 1.53 Mb. Скачать 1.53 Mb.
|
|
Метод замены переменной. Одним из основных методов интегрирования является метод замены переменной (или метод подстановки), описываемый следующей формулой: где Пример. Найти интегралы: а) Решение. а) Положим б) Положим в) Положим Метод интегрирования по частям. Пусть Формула интегрирования по частям используется для интегралов следующих типов интегралов: 1. 2. Пример. Найти интегралы: а) Решение. а) Так как Так как Теперь, применяя формулу интегрирования по частям, получаем: Используя метод разложения, убеждаемся, что полученный интеграл – сумма табличного и интеграла, который был определен при нахождении б) Пусть и Применяя формулу интегрирования по частям , получаем В) Пусть ЗАДАНИЯ ДЛЯ КОНТРОЛЬНЫХ РАБОТ (6 заданий по 25 вариантов) Вариант выбирается студентом в соответствии с последними двумя цифрами зачетной книжки. В случае, если две последние цифры превышают 25, то вариант выбирается по формуле: номер зачетки минус необходимое число раз по 25, пока разность не будет меньше или равна 25. Задание №1 Вычислить матрицу 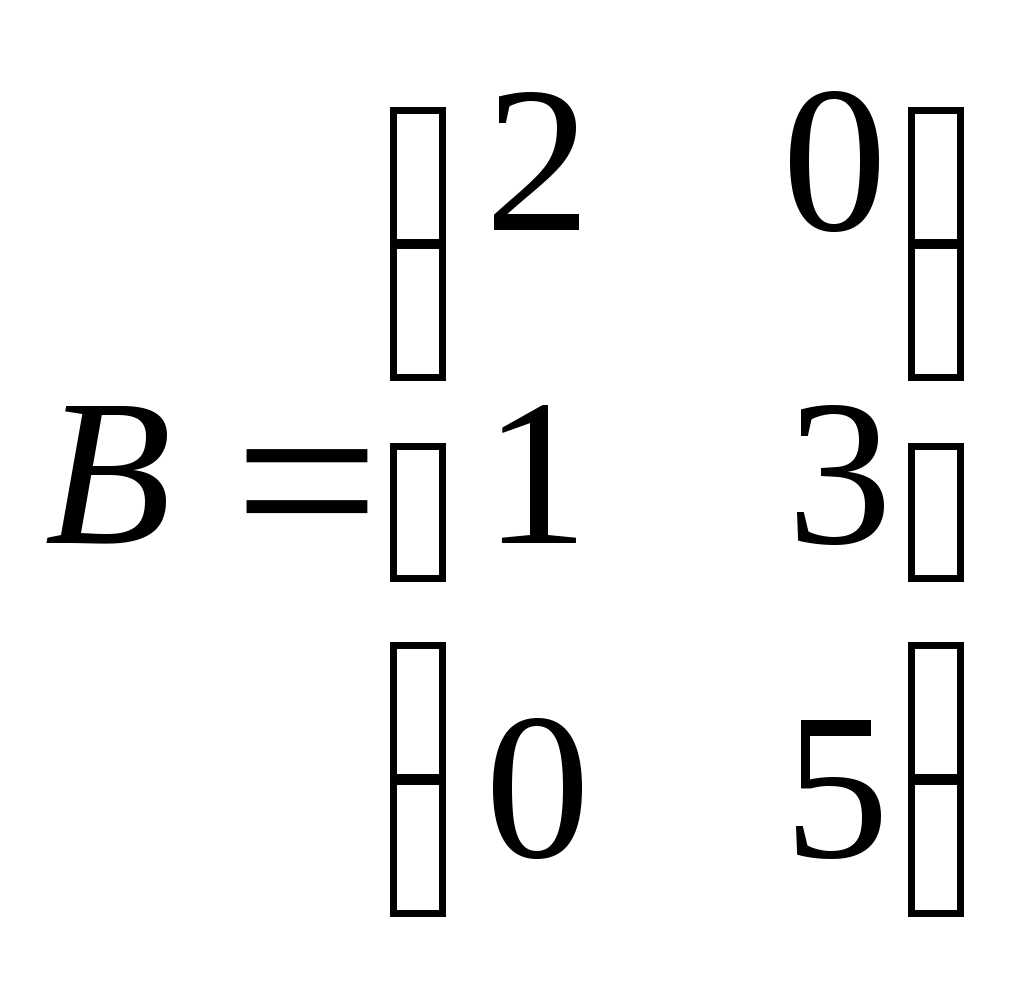 ; ; Найти произведение матриц Решить уравнение 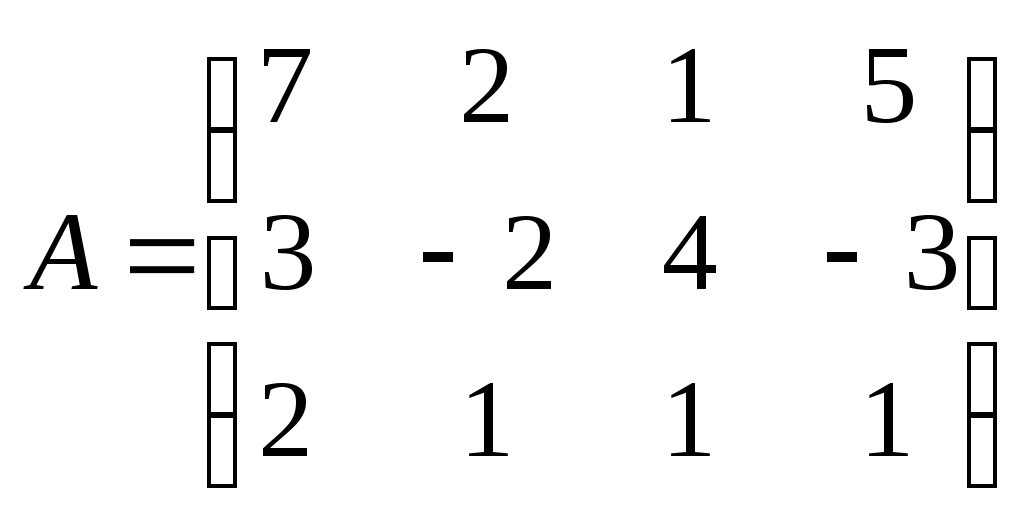 , , 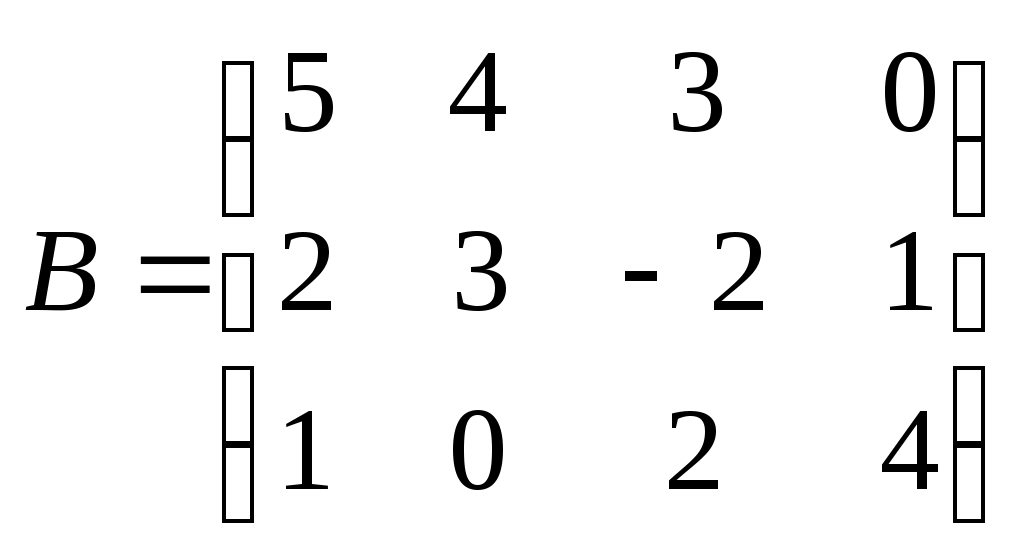 . .Вычислить матрицу 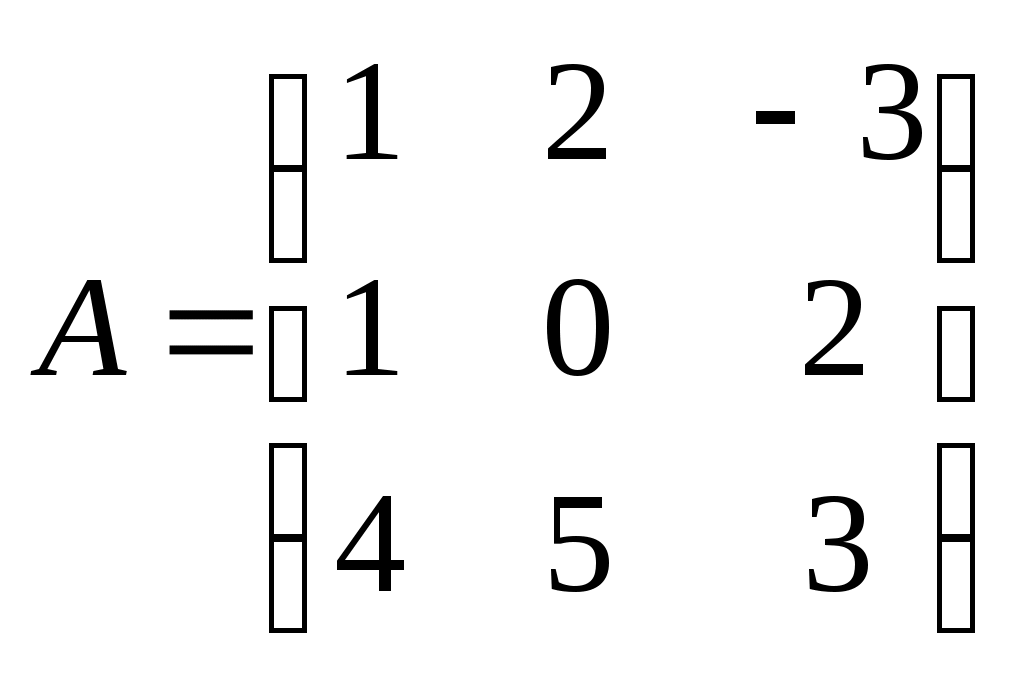 ; ; 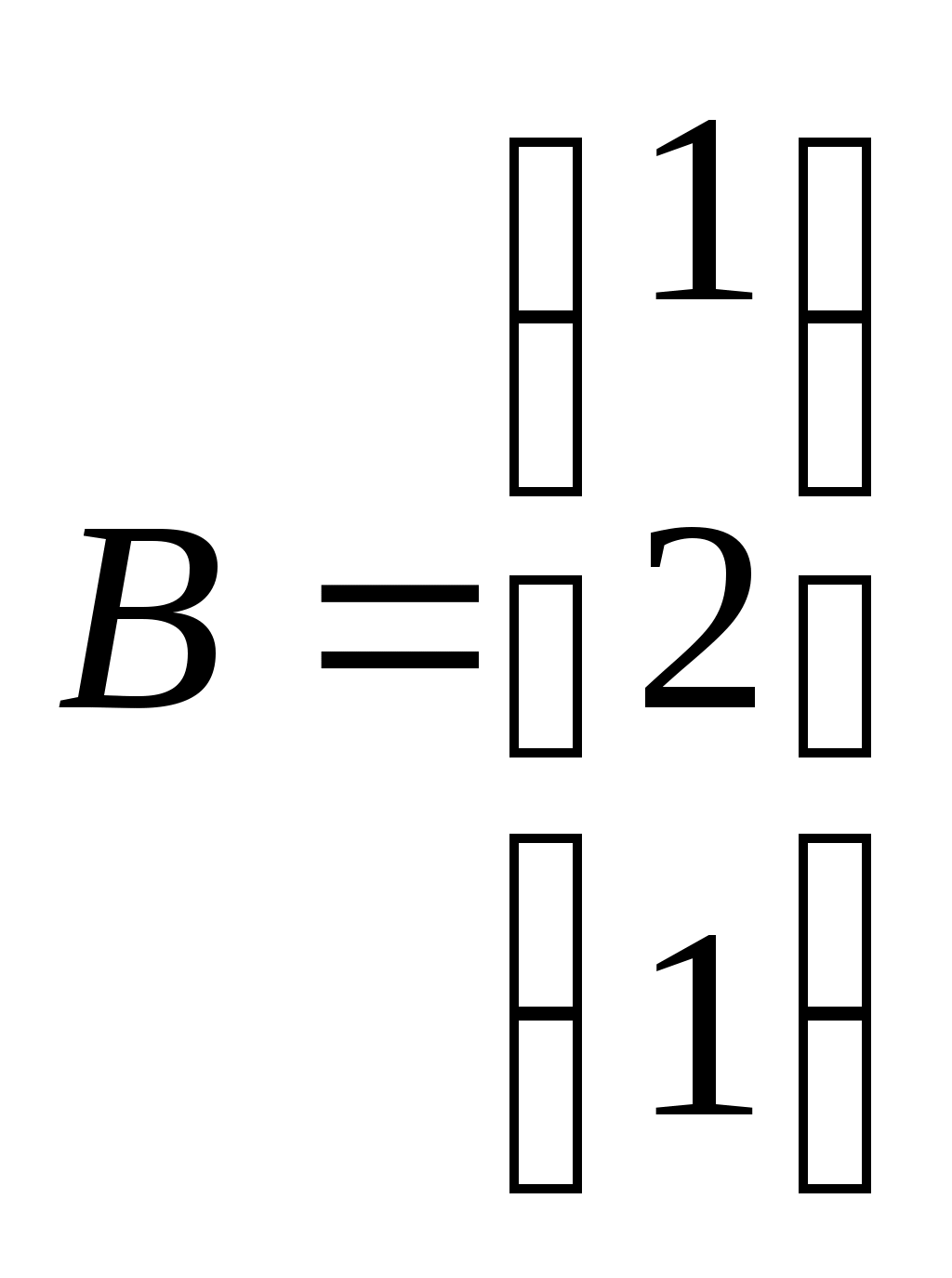 ; ; Найти произведение матриц 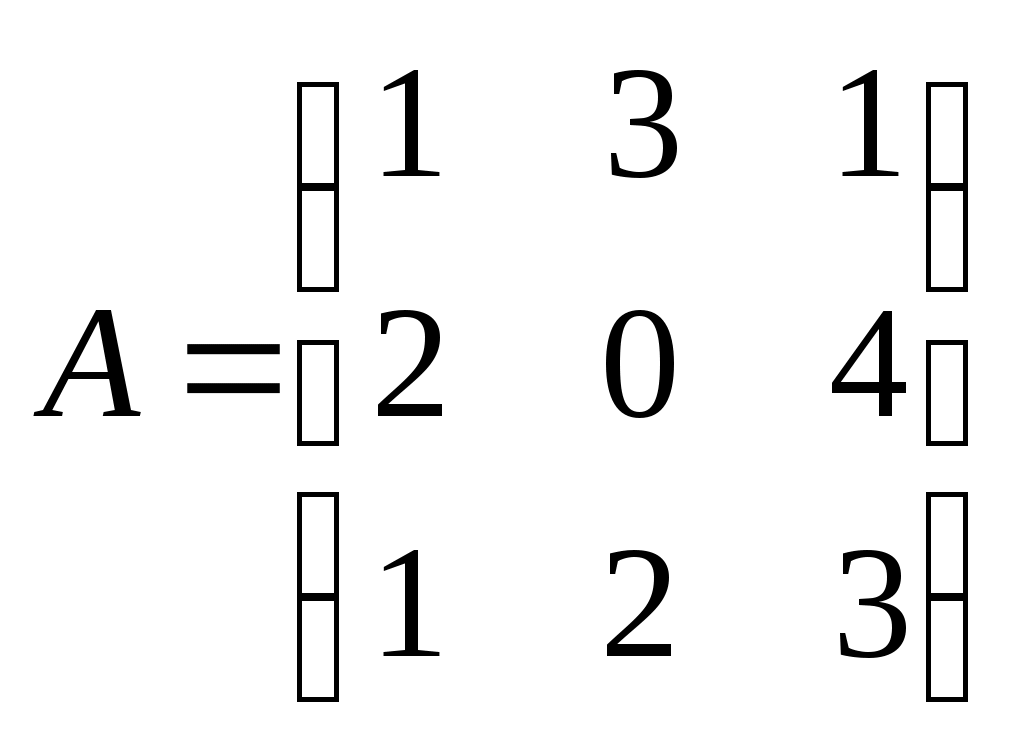 , , 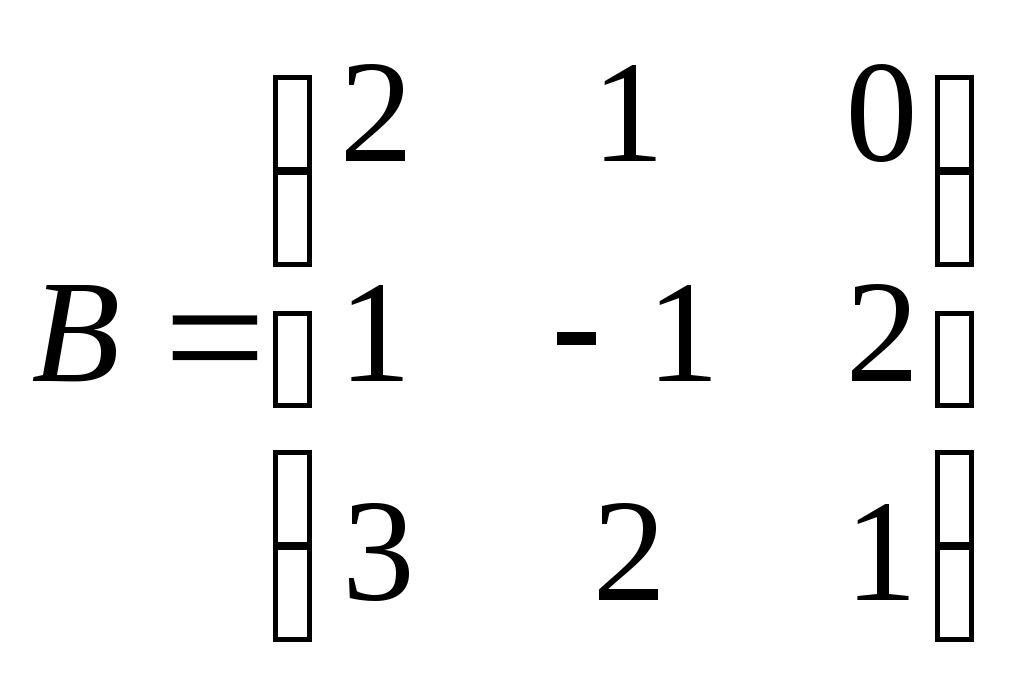 . .Найти произведение матриц 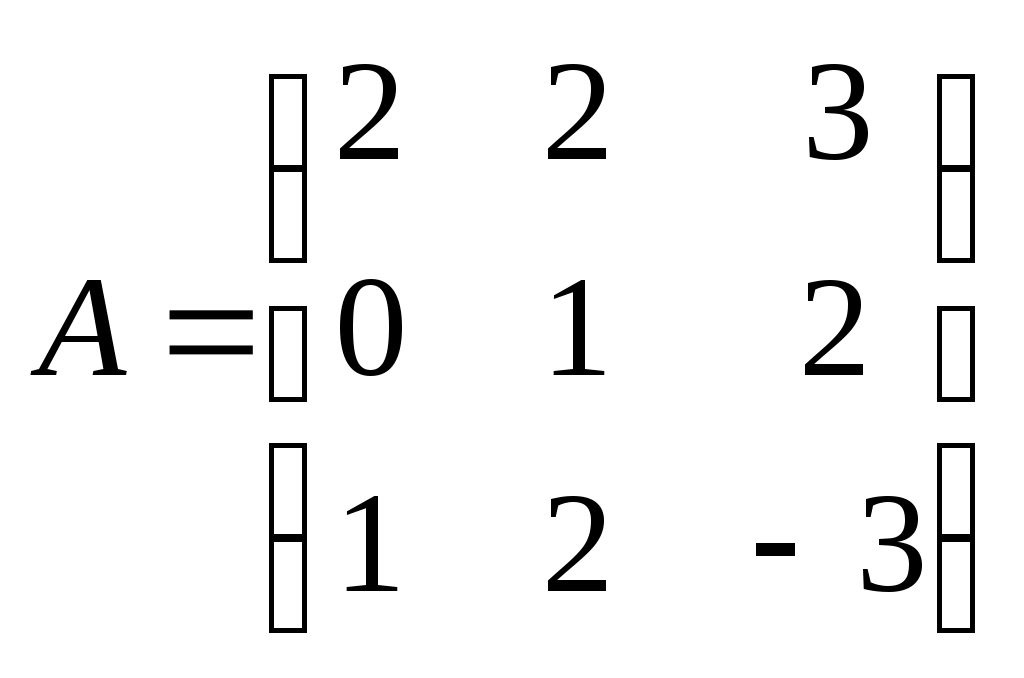 , , 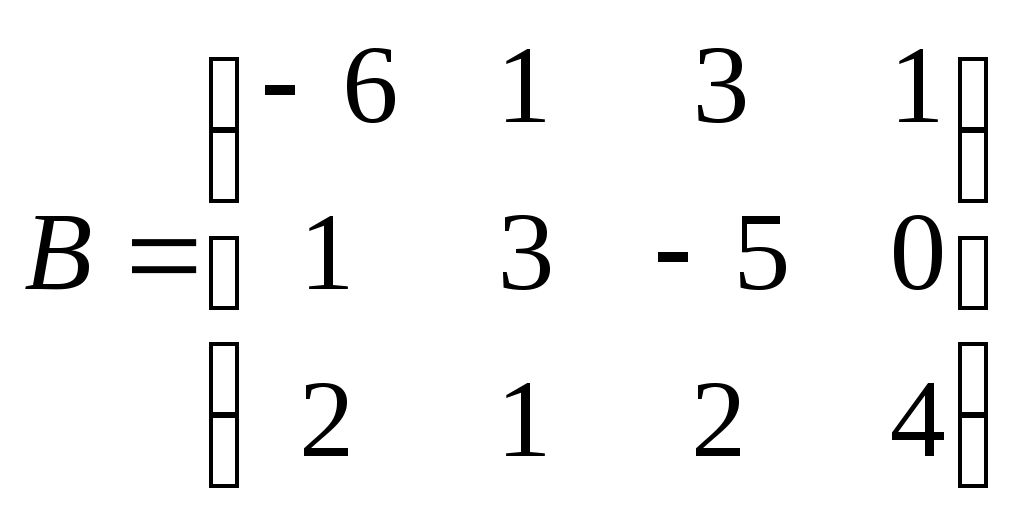 . .Найти произведение матриц 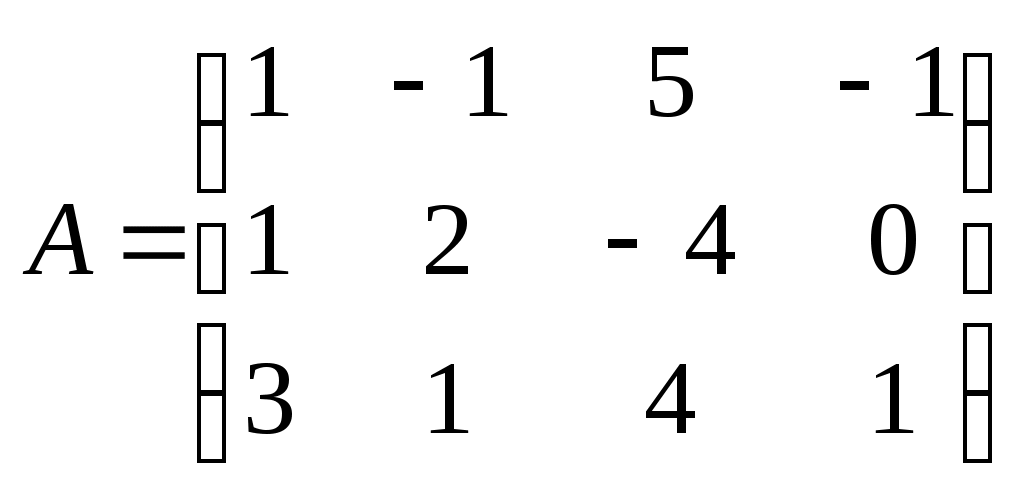 , , 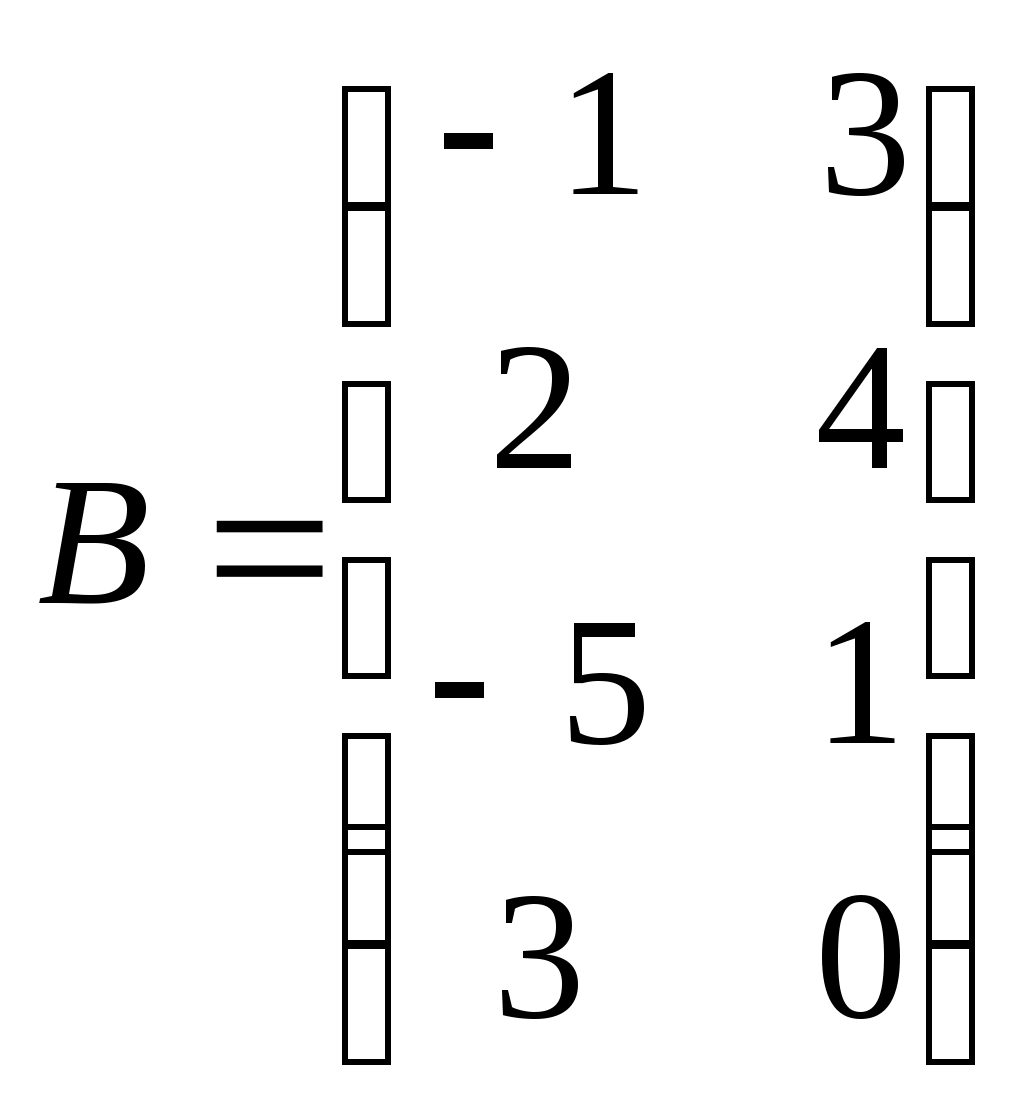 . .Найти значение матричного многочлена 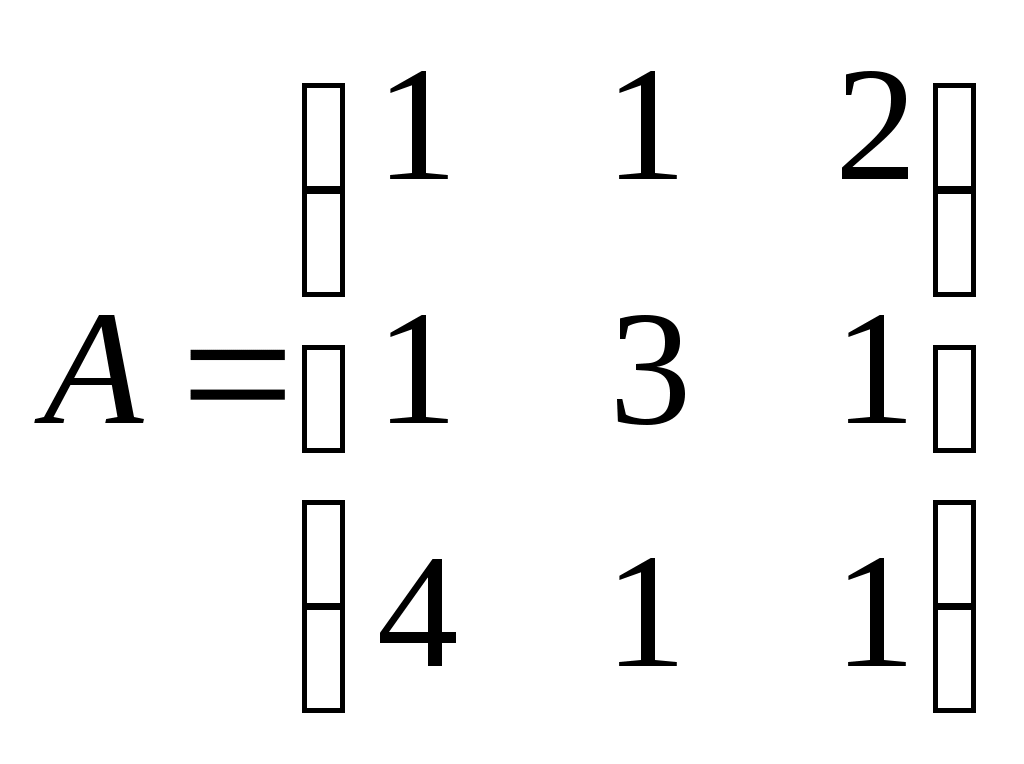 , , Найти произведение матриц 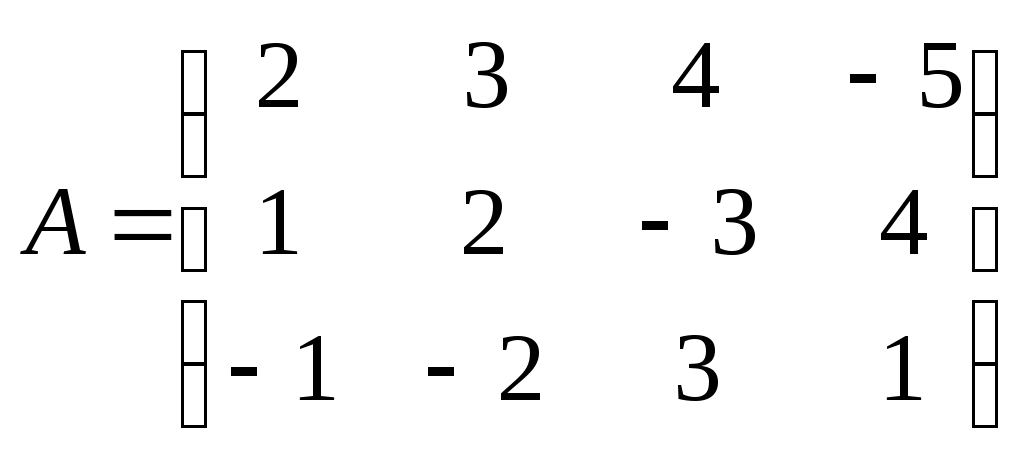 , , 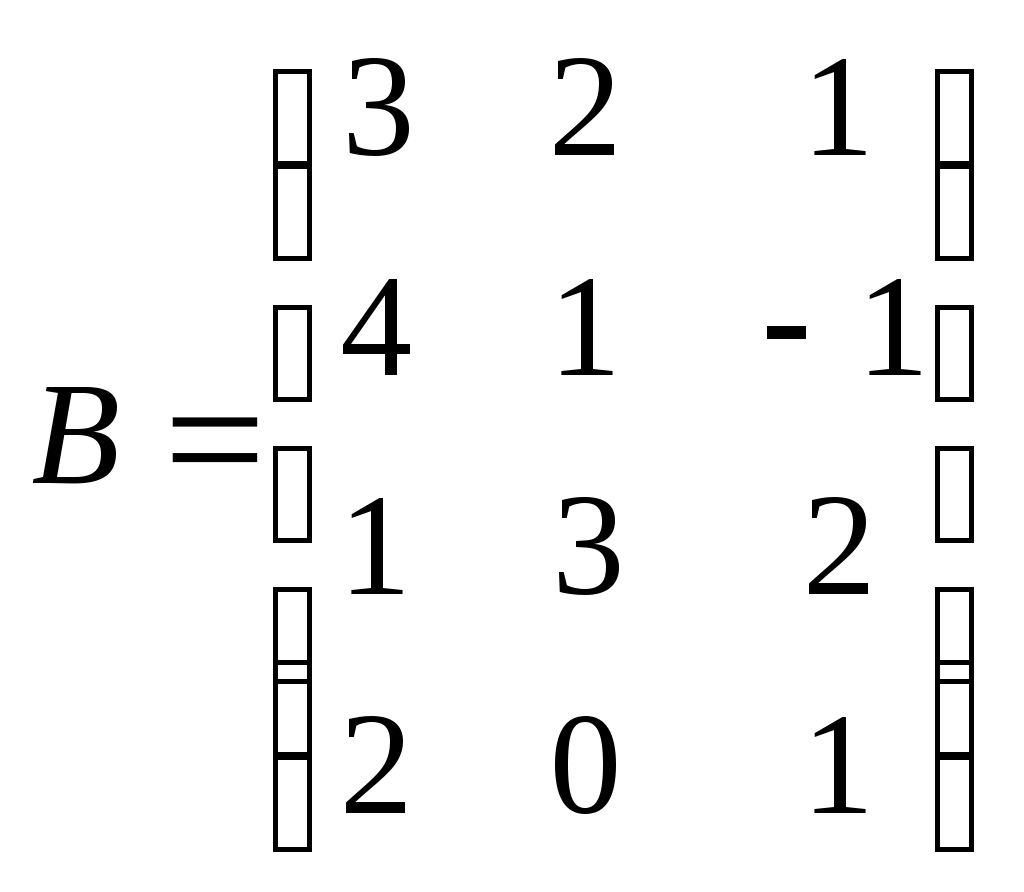 . .10. Найти произведение матриц 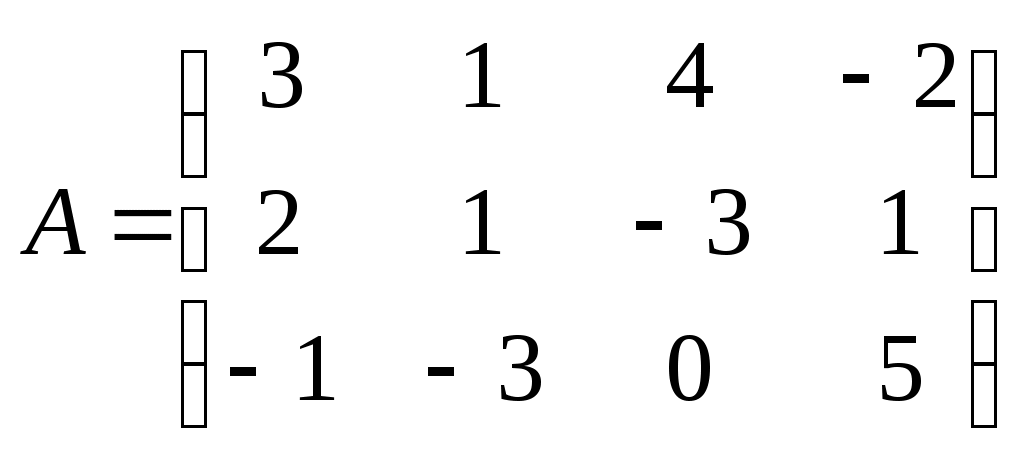 , , 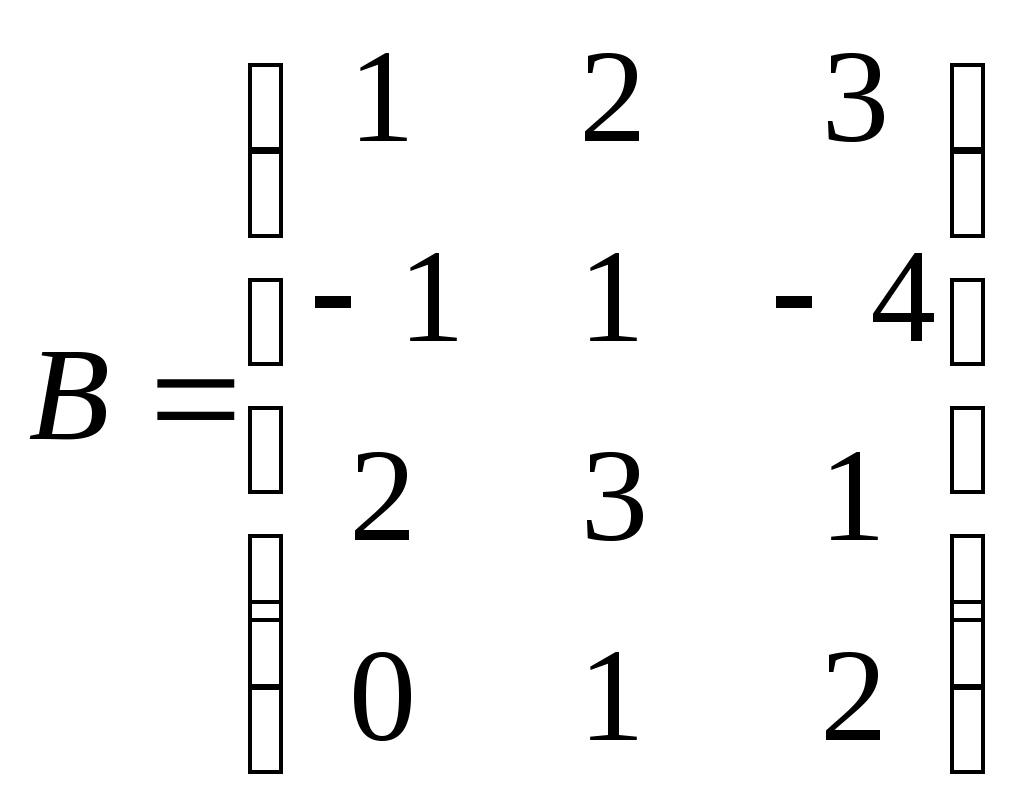 . .11. Найти произведение матриц 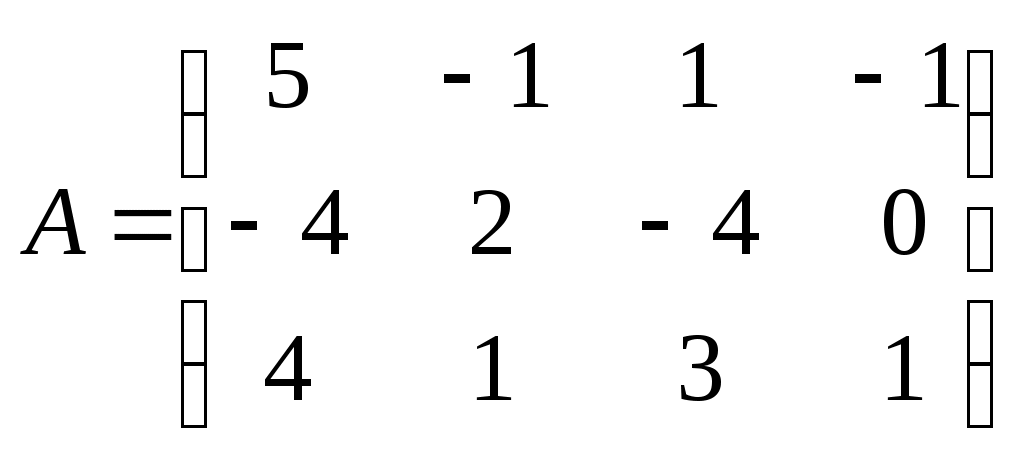 , , 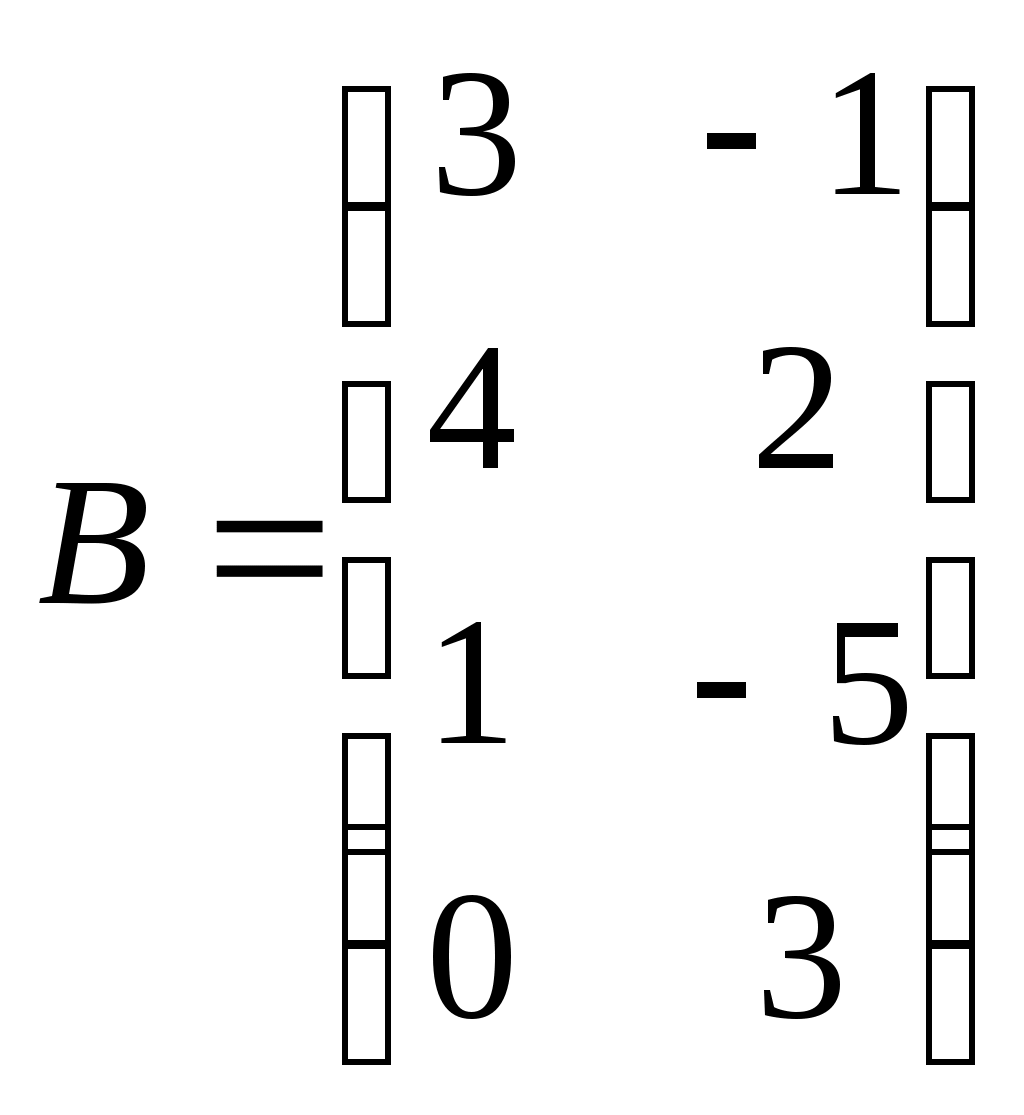 . .12. Найти значение матричного многочлена 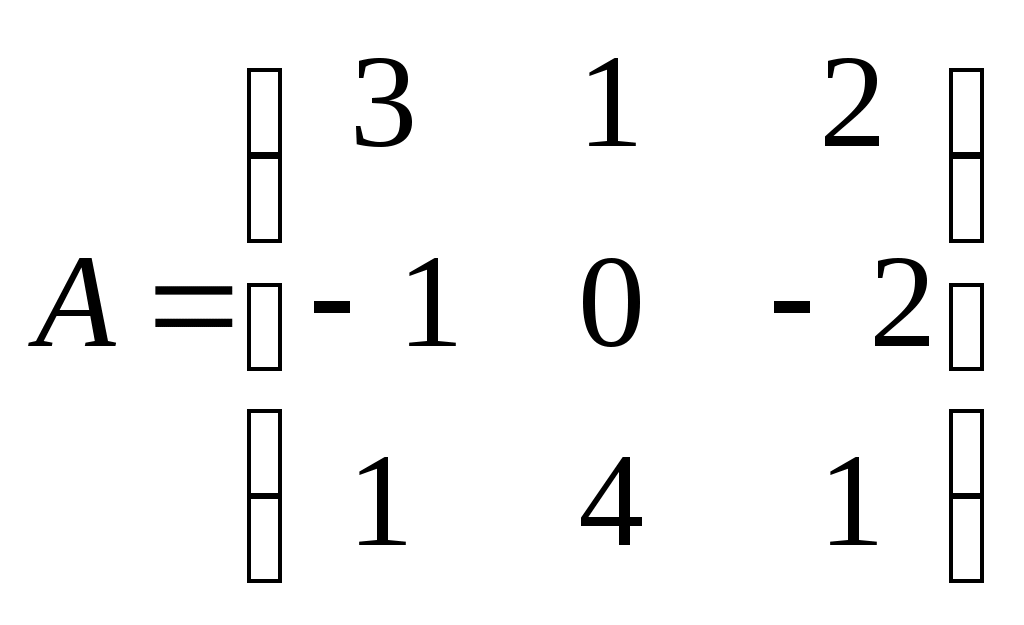 , , 13. Вычислить матрицу 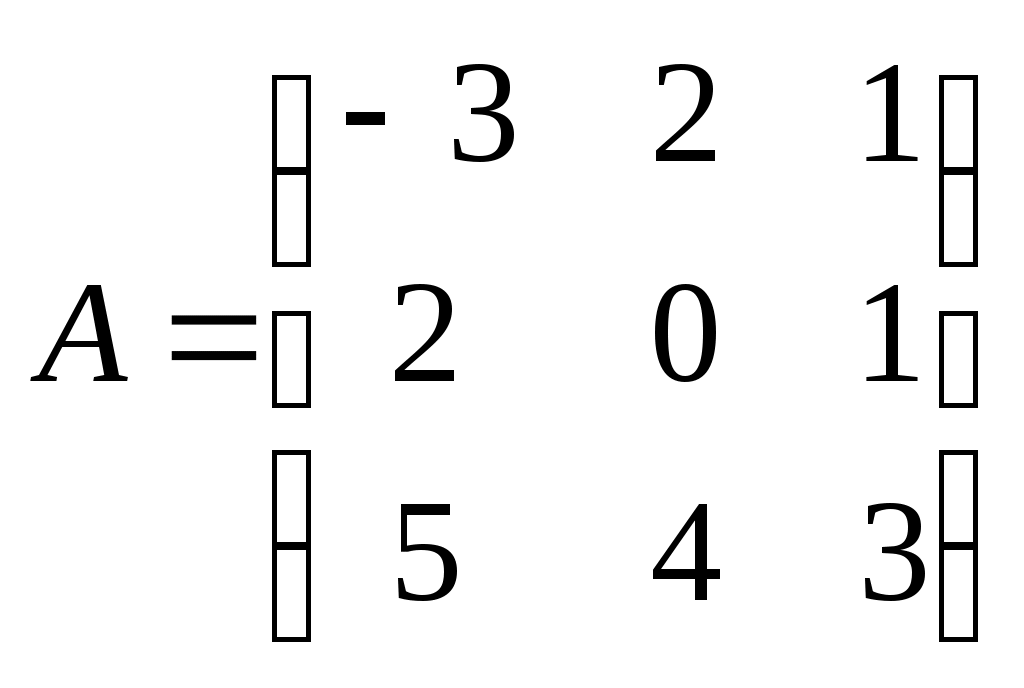 ; ; 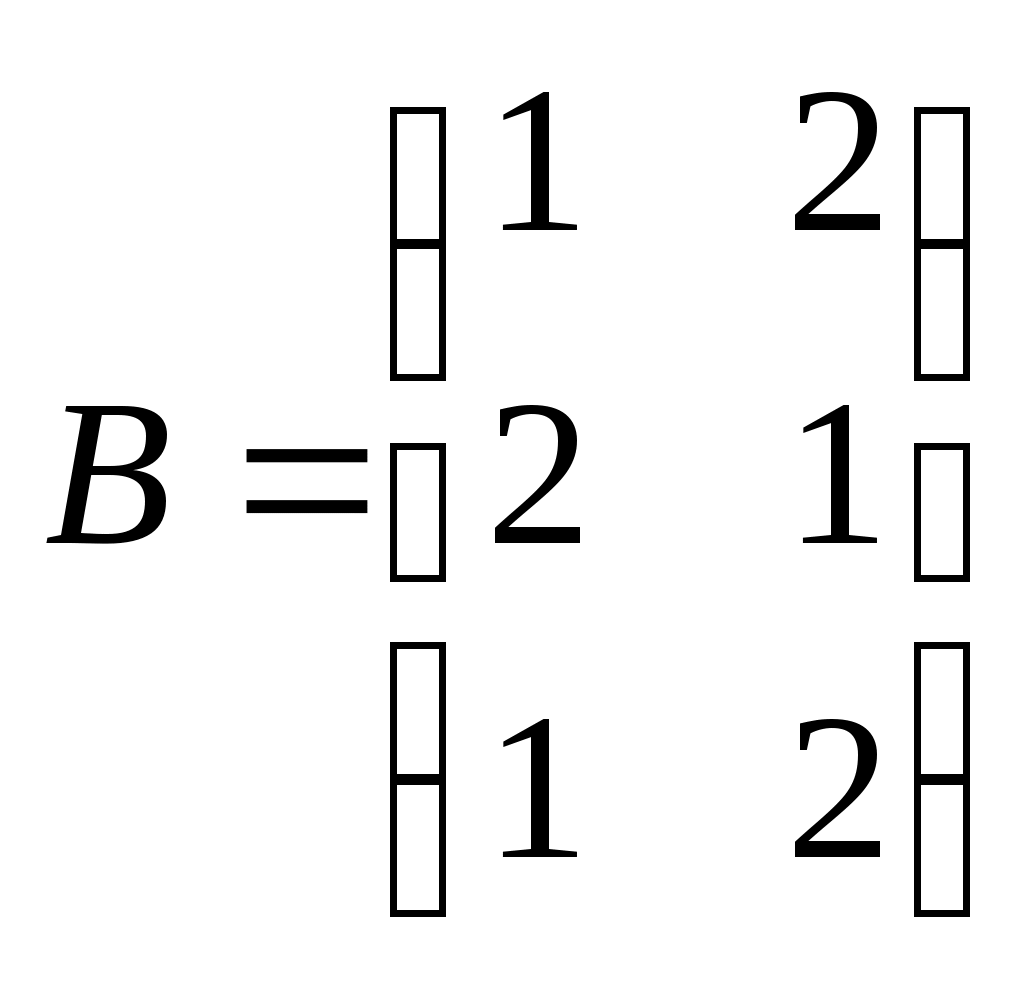 ; ; 14. Решить уравнение 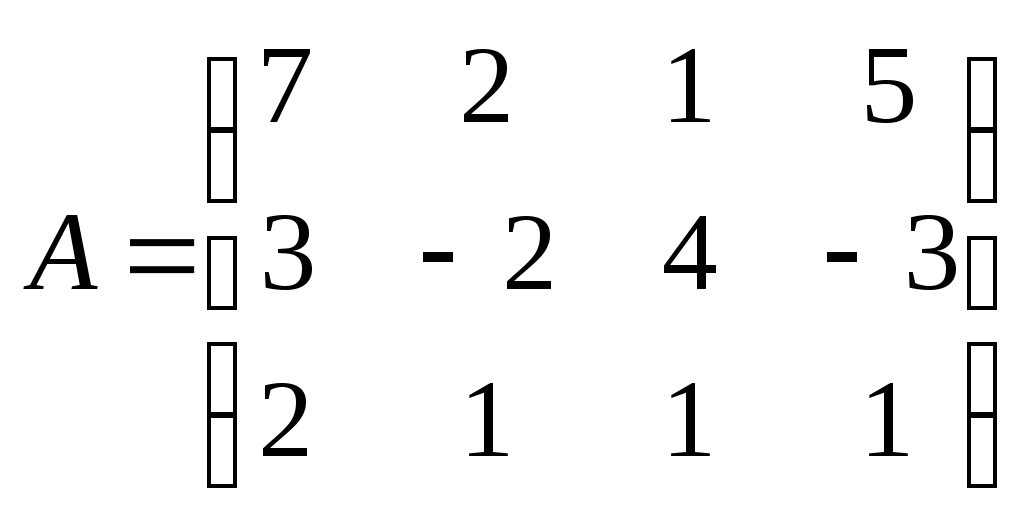 , , 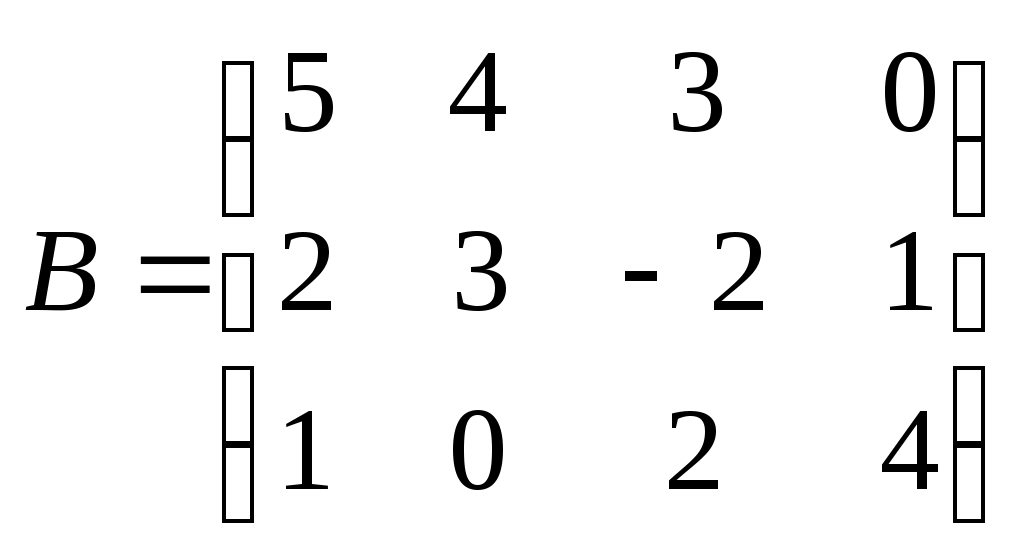 . .15. Найти произведение матриц 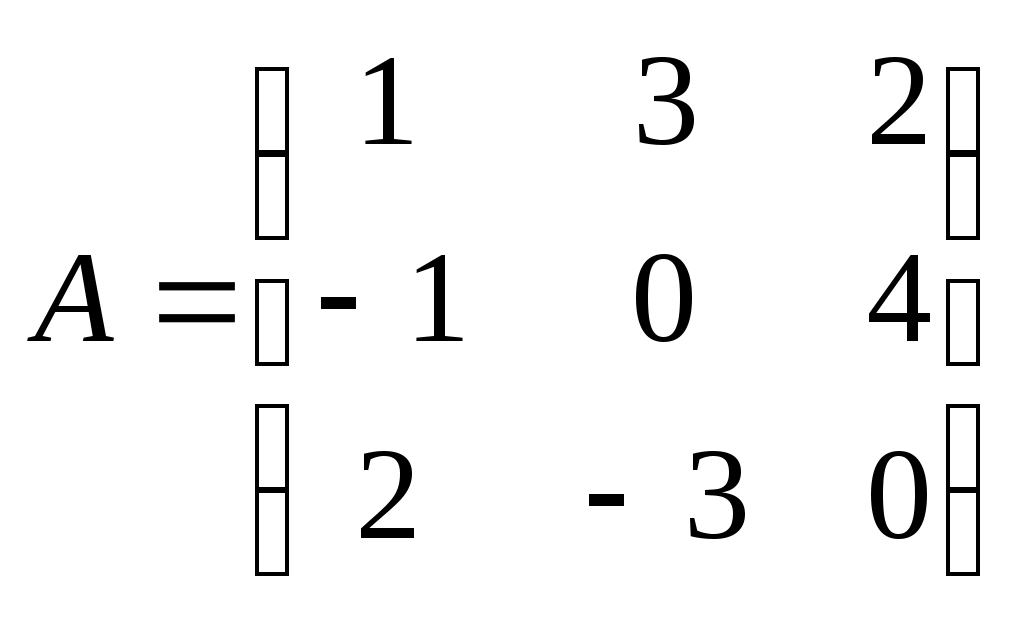 , ,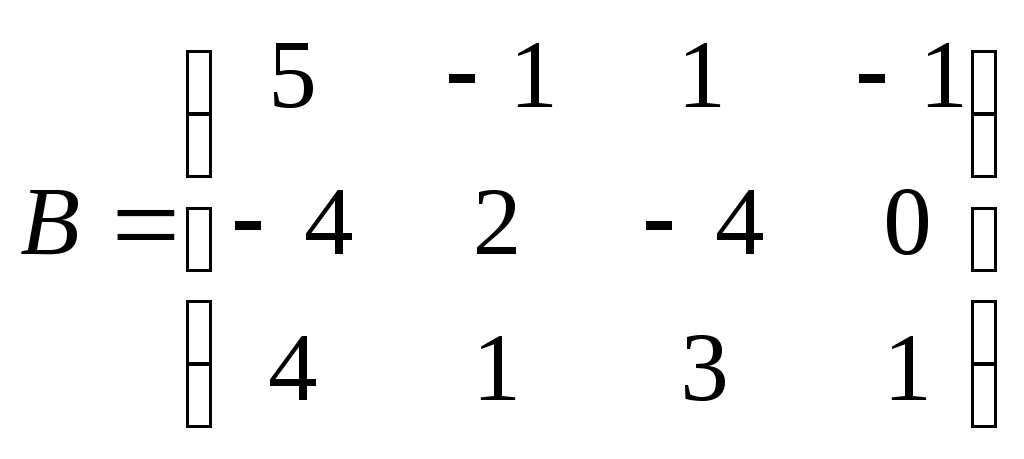 . .16. Найти произведение матриц 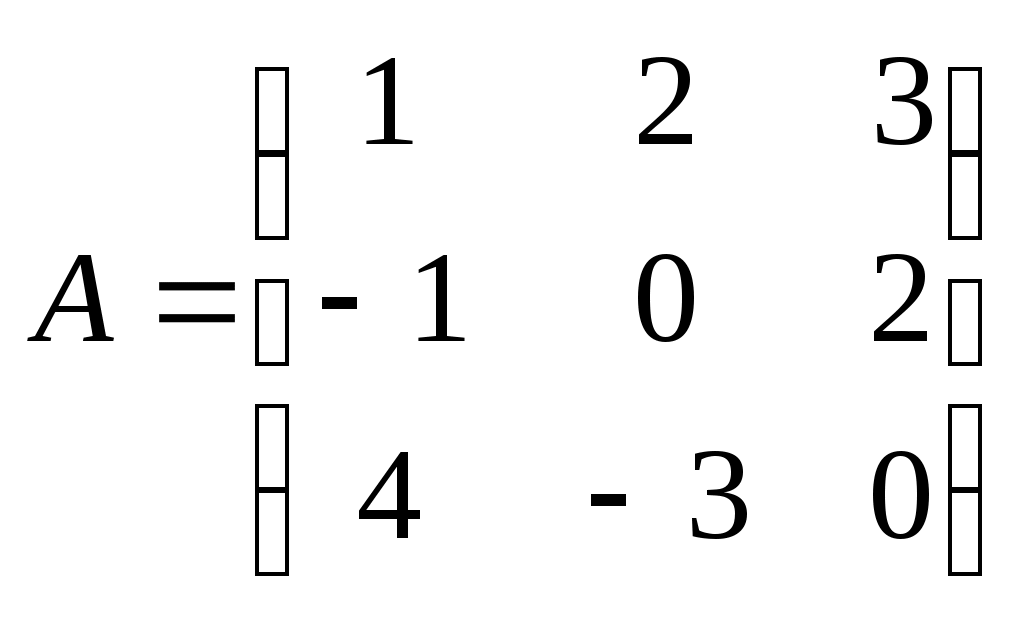 , ,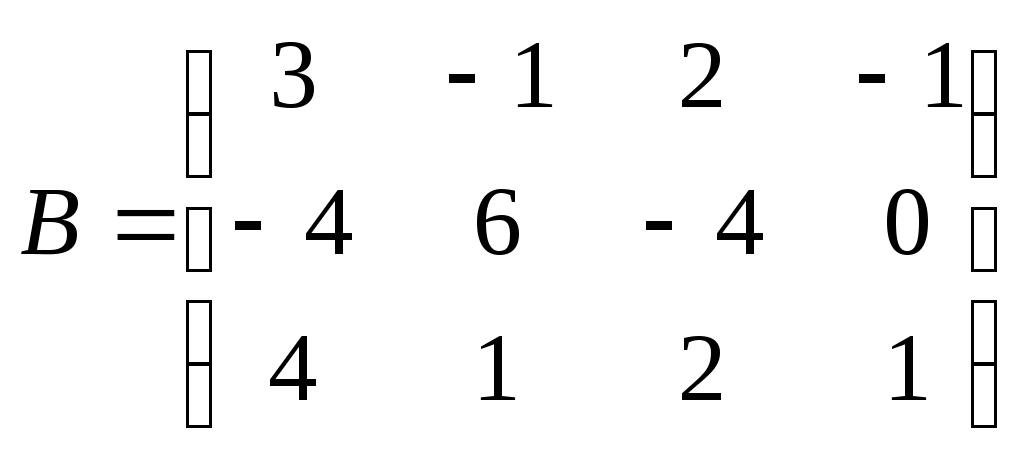 . .17. Найти произведение матриц 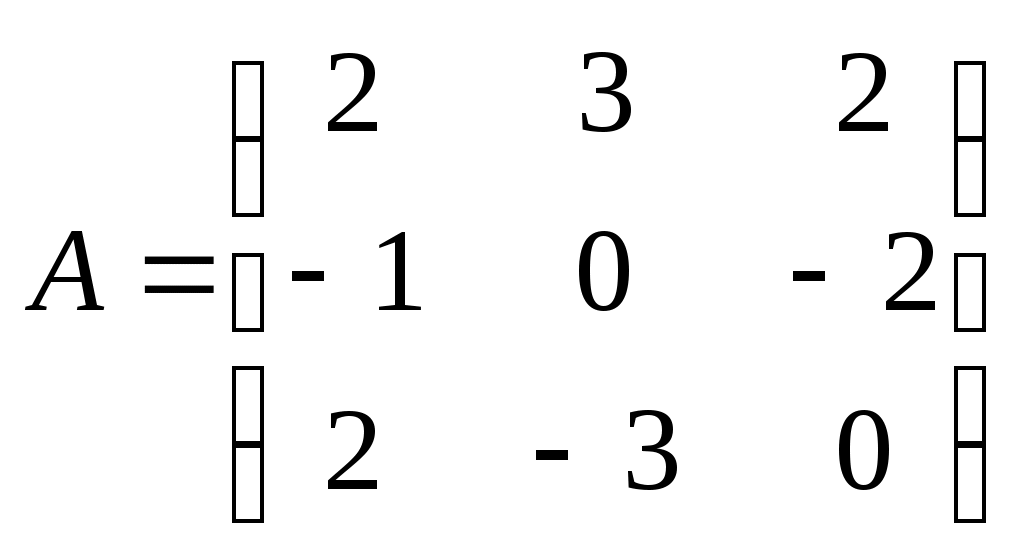 , ,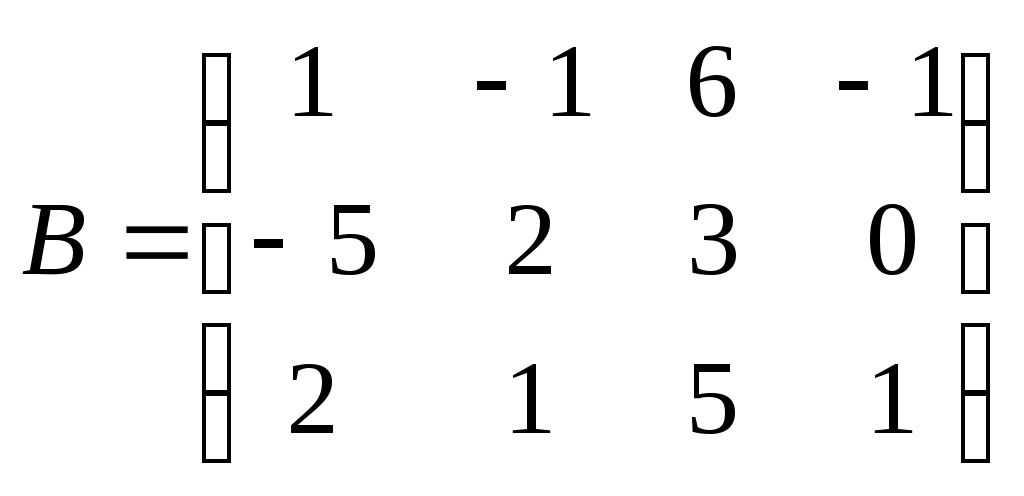 . .18. Найти произведение матриц 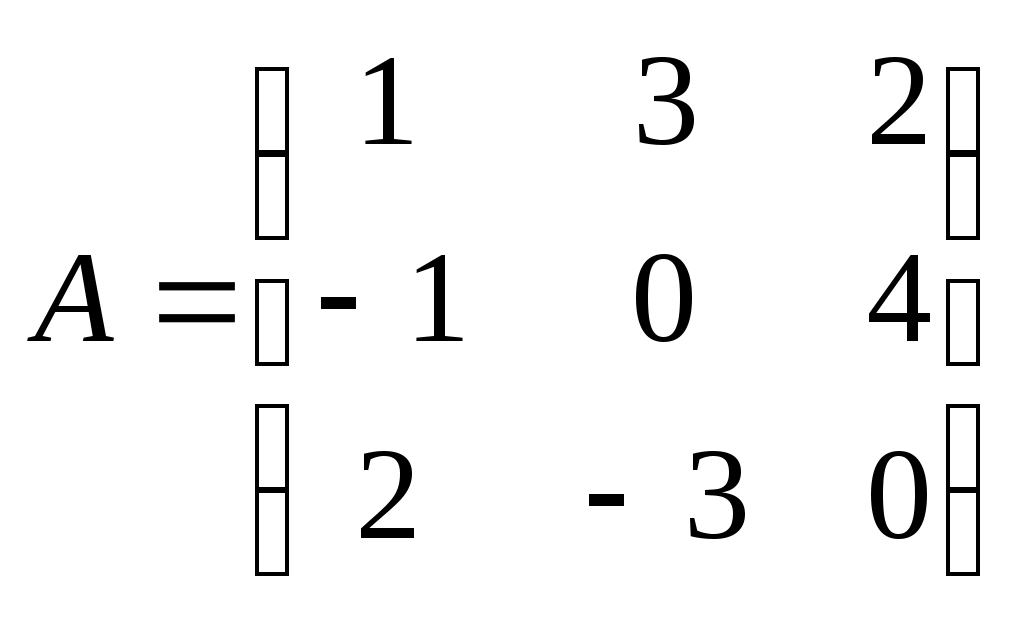 , ,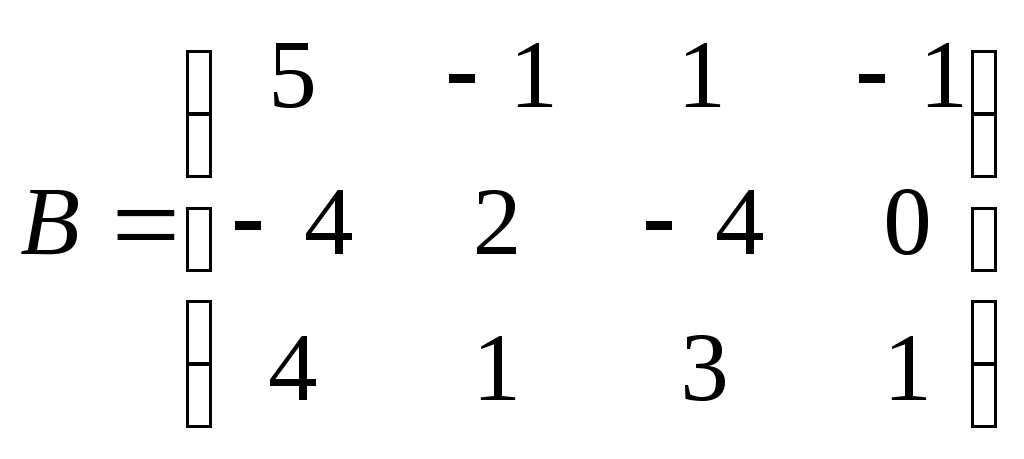 . .19. Найти произведение матриц 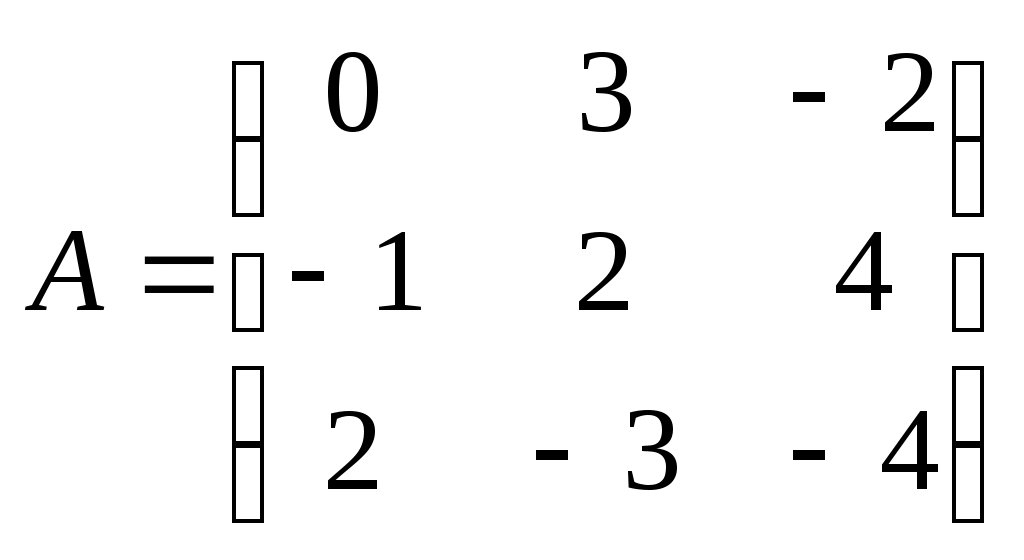 , ,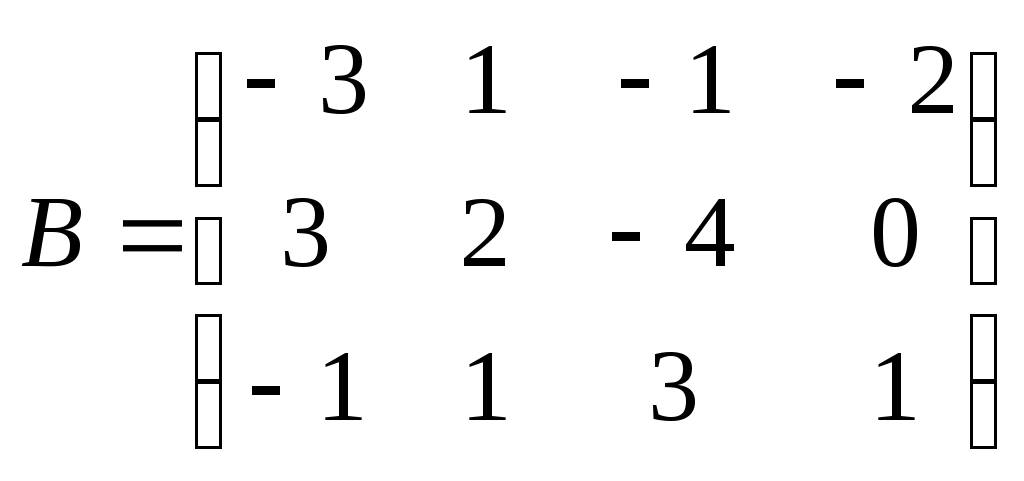 . .20. Найти произведение матриц 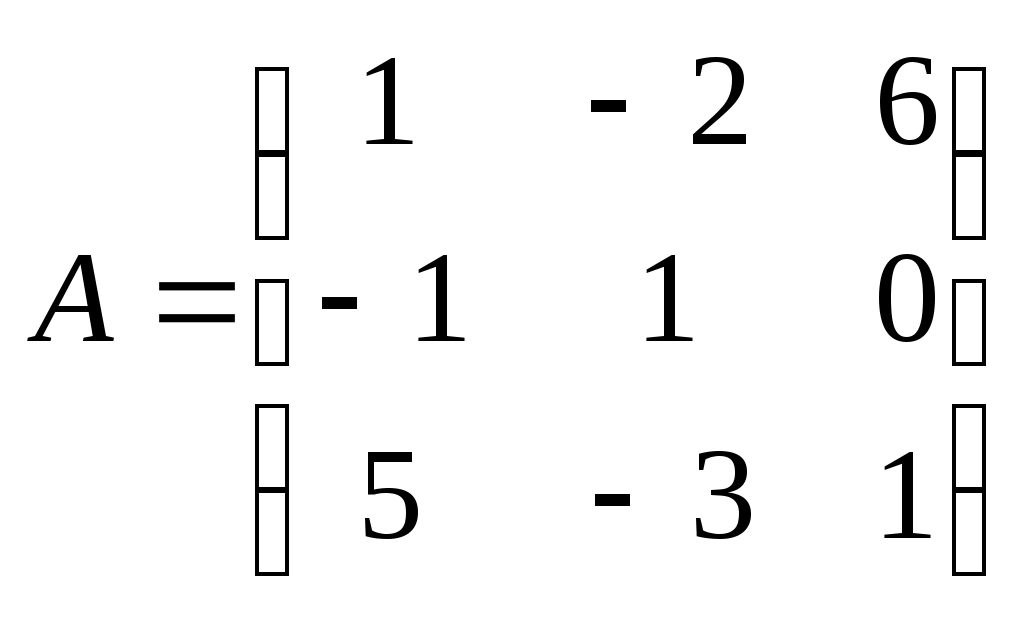 , ,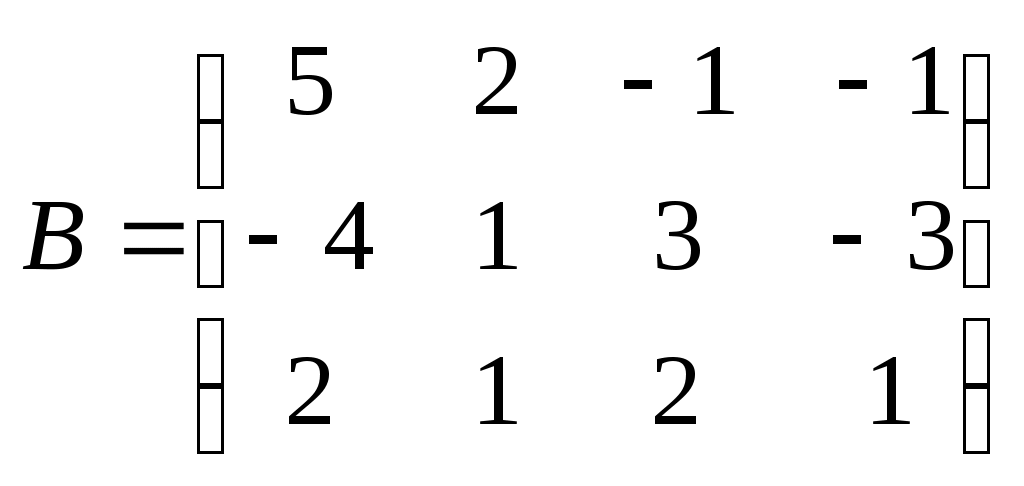 . .21. Найти произведение матриц 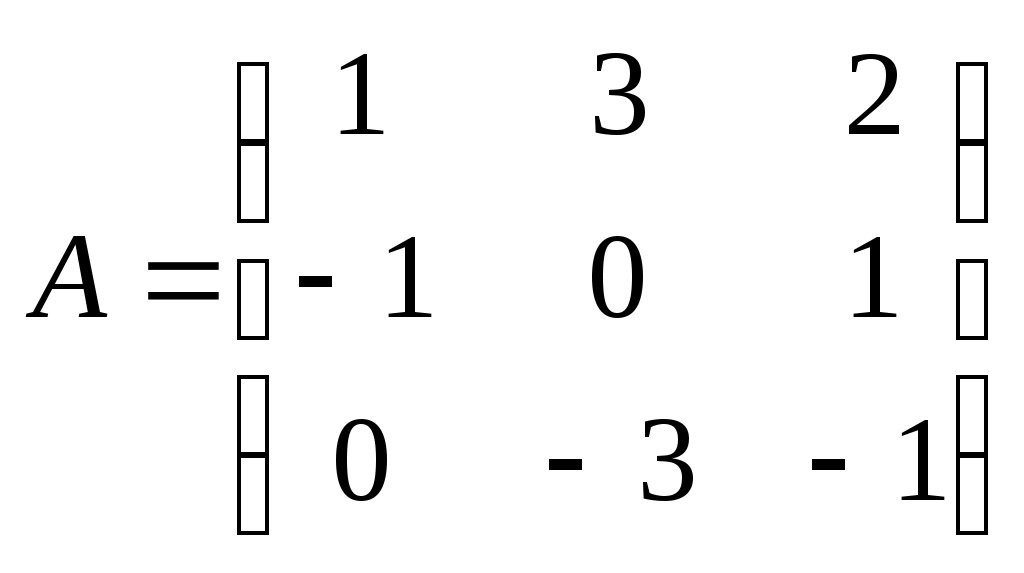 , ,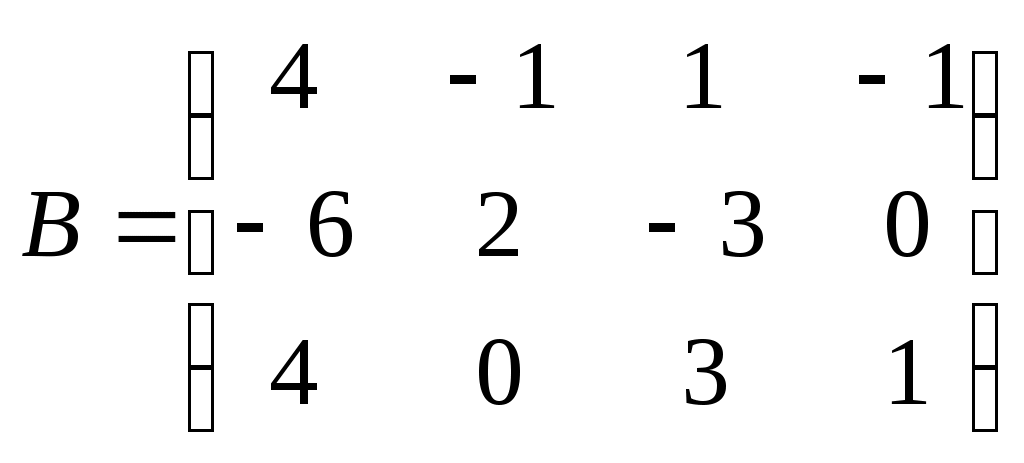 . .22. Найти произведение матриц 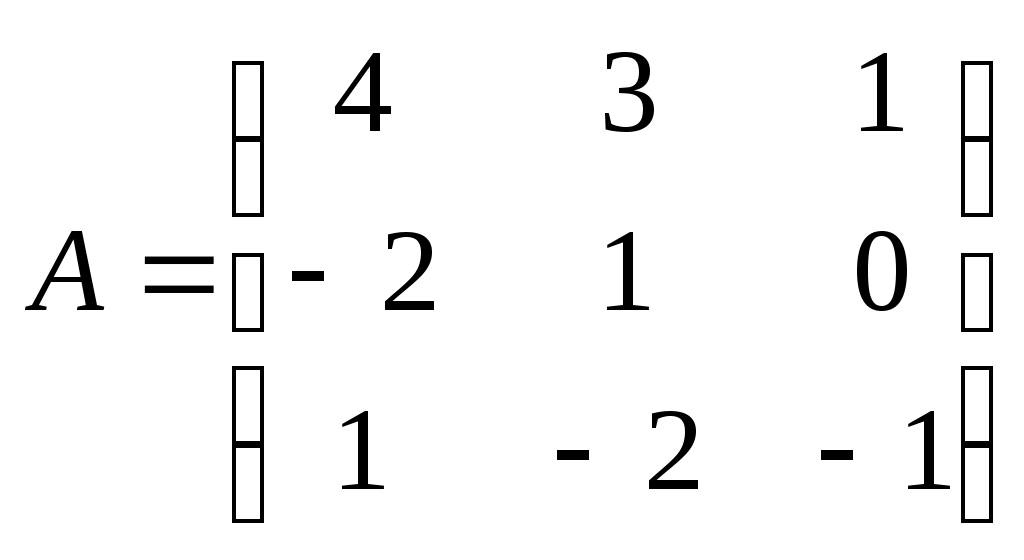 , ,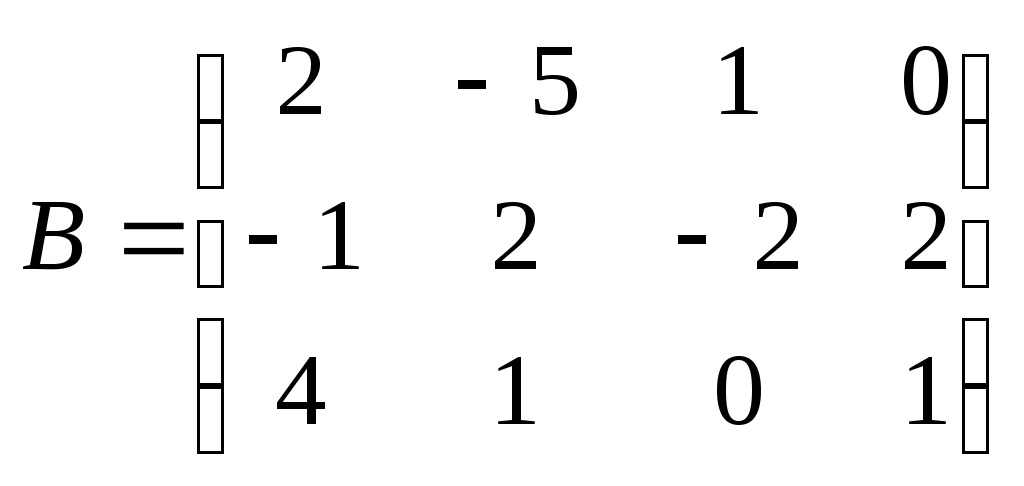 . .23. Найти произведение матриц 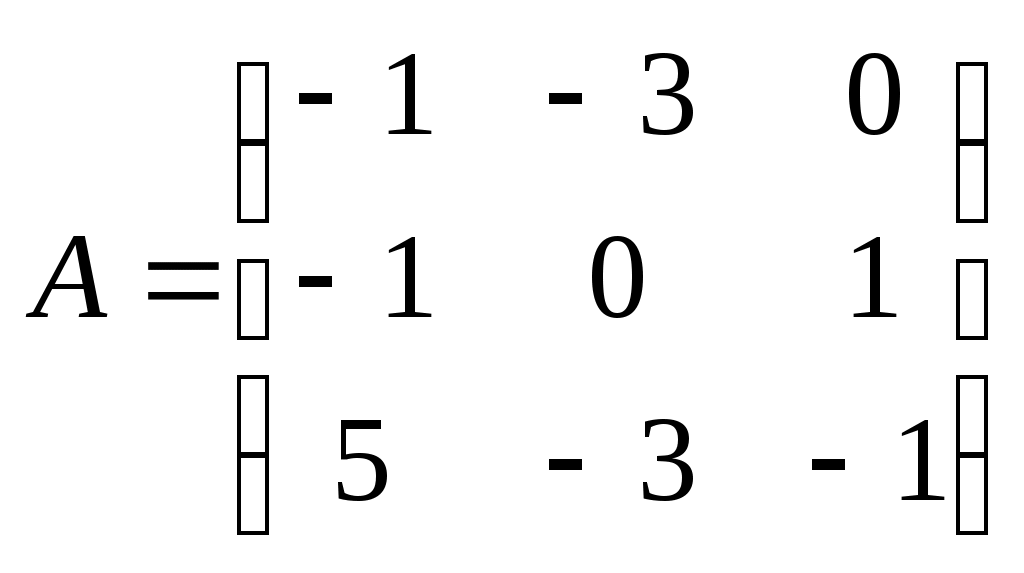 , ,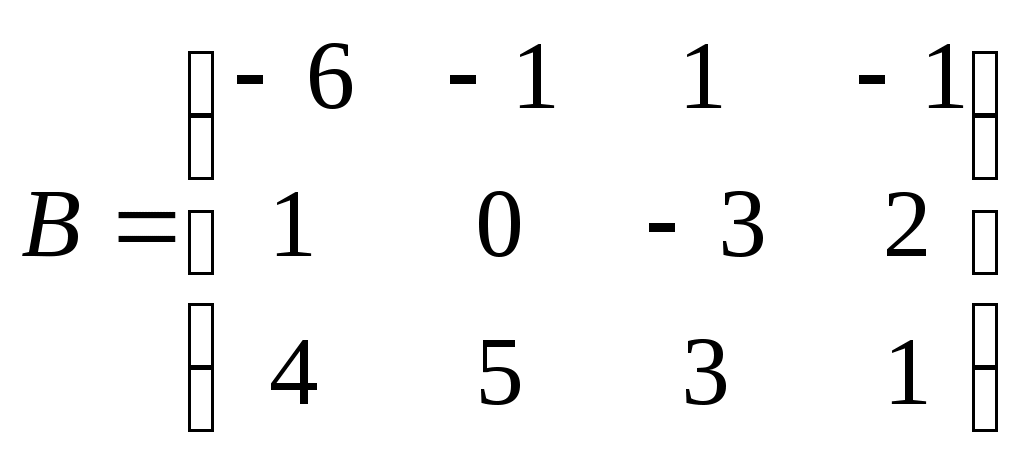 . .24. Найти произведение матриц  , ,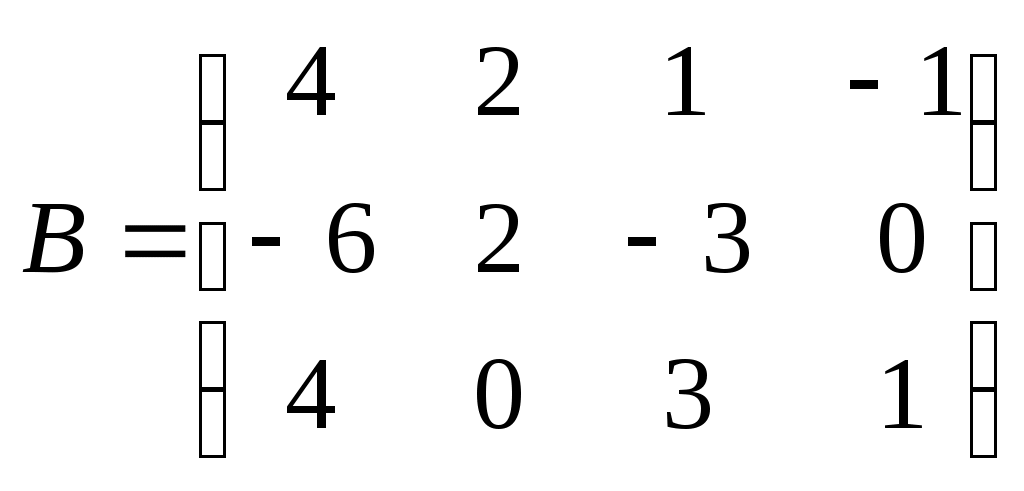 . .25. Найти произведение матриц 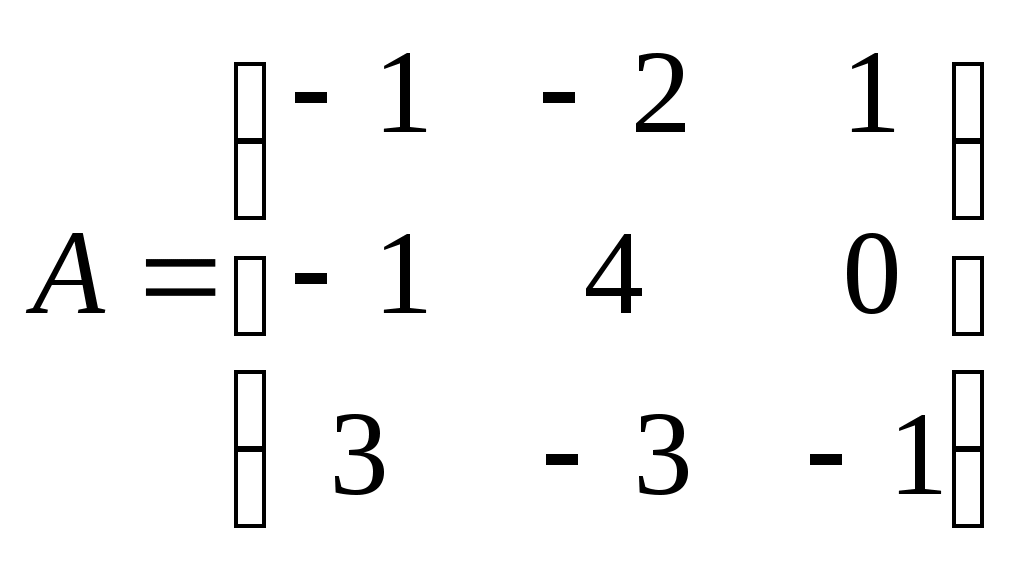 , ,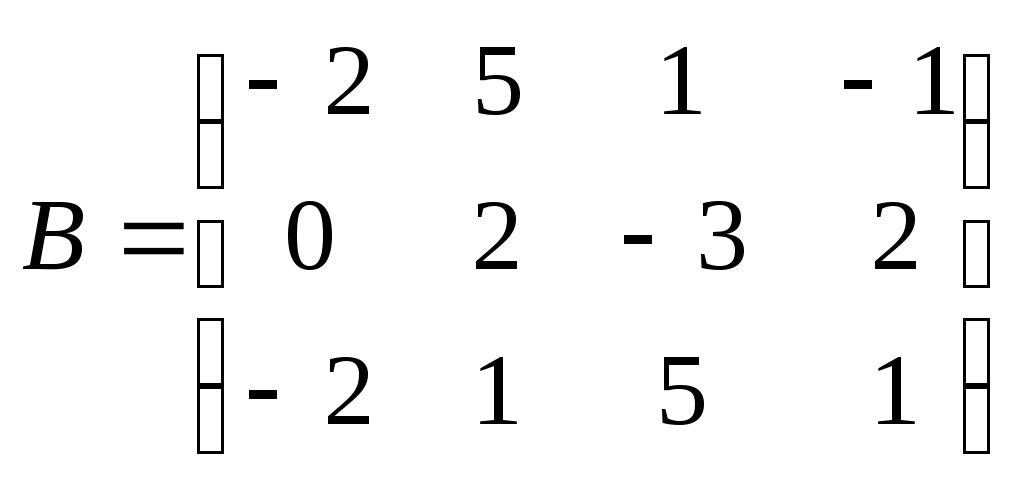 . . |
