Матем. КР1 для психологов. Матрицы. Операции над матрицами
 Скачать 1.53 Mb.
|
|
Обратная матрица. Матрица  называется обратной по отношению к квадратной матрице  , если при умножении этой матрицы на данную как слева, так и справа получается единичная матрица: .Только квадратная матрица имеет обратную, причем тогда и только тогда, когда определитель исходной матрицы отличен от нуля. Алгоритм вычисления обратной матрицы. Находим определитель исходной матрицы. Если  , то матрица вырожденная и обратная матрица не существует. Если  , то обратная матрица существует.Находим матрицу  , транспонированную к .Находим алгебраические дополнения элементов транспонированной матрицы  (i=1,2,…,n; j=1,2,…,n) и составляем из них присоединенную матрицу  (i=1,2,…,n; j=1,2,…,n).Вычисляем обратную матрицу по формуле:  .Проверяем правильность вычисления обратной матрицы , исходя из ее определения: .Пример. Найти матрицу, обратную к данной:  .Определитель матрицы  , т.е. матрица – невырожденная и обратная матрица существует.Находим матрицу , транспонированную к :  .Находим алгебраические дополнения элементов матрицы и составляем из них присоединенную матрицу  : ;  ;  ; ;  ;  ; ;  ;  . .Вычисляем обратную матрицу : .СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ. Система  линейных уравнений с  переменными имеет вид: , 1)где  – произвольные числа, называемые, соответственно коэффициентами при переменных и свободными членами уравнений.Решением системы линейных уравнений называется такая совокупность чисел  , при подстановке которых каждое уравнение системы обращается в верное равенство.Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений. Совместная система уравнений называется, если она имеет единственное решение, и неопределенной, если она имеет более одного решения. Две системы уравнений называются равносильными, или эквивалентными, если они имеют одно и то же множество решений. Система линейных уравнений может быть записана в матричном виде. Обозначим: 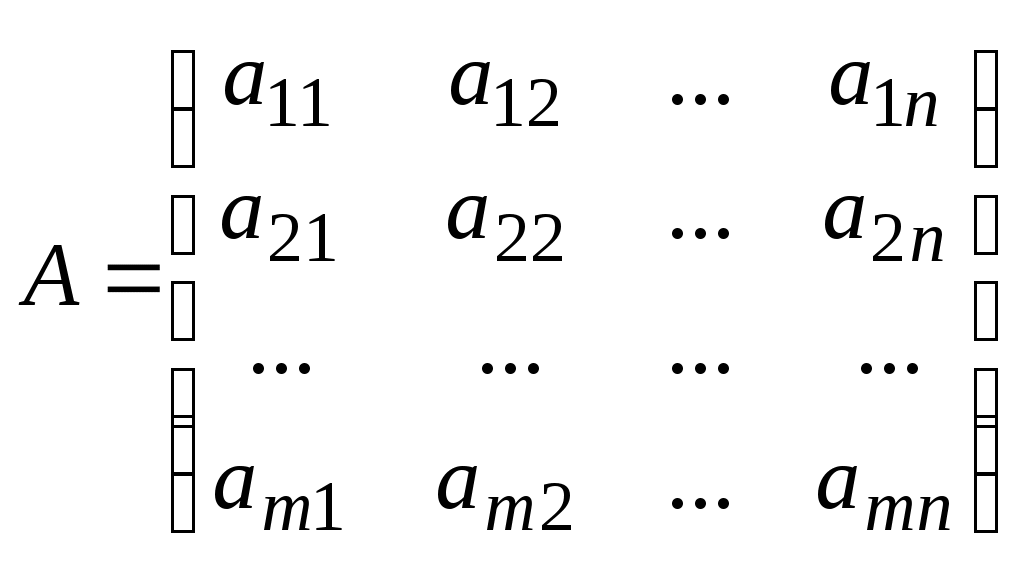 ;  ;  ,где – матрица коэффициентов при переменных, или матрица системы,  – матрица-столбец переменных;  – матрица-столбец свободных членов. Тогда система линейных уравнений может быть записана в виде: .Пусть число уравнений системы равно числу переменных. Тогда матрица системы является квадратной, а ее определитель  называется определителем системы.Метод обратной матрицы. Предположим, что квадратная матрица системы  невырожденная, т.е. ее определитель . В этом случае существует обратная матрица .Умножая слева обе части матричного равенства на матрицу , получим  . Так как  , то решением системы методом обратной матрицы будет матрица-столбец .Метод Крамера. Теорема Крамера. Пусть  – определитель матрицы системы , а  – определитель матрицы, получаемой из матрицы заменой  -го столбца столбцом свободных членов. Тогда, если  , то система имеет единственное решение, определяемое по формулам: .Формулы для  называются формулами Крамера.Пример. Решить систему уравнений  ,а) методом обратной матрицы; б) по формулам Крамера. а) Обозначим ;  ;  .Найдем определитель  . Так как , то матрица невырожденная и существует обратная матрица .Получим  . Теперь по формуле  .То есть решение системы  .б) Найдем определитель системы  . Так как , то по теореме Крамера система имеет единственное решение.Вычислим определители матриц  , полученных из матрицы  заменой соответственно первого, второго и третьего столбцов на столбец свободных членов: ;  ;  .Теперь по формулам Крамера находим  ;  ;  .То есть решение системы .Метод Гаусса. Метод Гаусса – метод последовательного исключения переменных – заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находят все остальные переменные. Предположим, что в системе уравнений коэффициент при переменной  в первом уравнении  (Если это не так, то перестановкой местами уравнений добьемся того, что ).Шаг 1. Умножая первое уравнение на подходящие числа (а именно на  ,  , …,  ) и прибавляя полученные уравнения соответственно ко второму, третьему ,…, -тому уравнению системы, исключим переменную из всех последующих уравнений, начиная со второго. Получим , где буквами с верхним индексом (1) обозначены новые коэффициенты, полученные после первого шага. Шаг 2. Предположим, что  (если это не так, то соответствующей перестановкой уравнений или переменных с изменением их номеров добьемся того, чтобы ).Умножая второе уравнение на подходящие числа (  , , …,  ) и прибавляя полученные уравнения соответственно к третьему, четвертому,…, -тому уравнению системы, исключим переменную  из всех последующих уравнений, начиная с третьего.Продолжая процесс последовательного исключения переменных, после (  )-го шага получим систему (2)Число нуль в последних  уравнениях означает, что их левые части имеют вид  . Если хотя бы одно из чисел  ,…, не равно нулю, то соответствующее равенство противоречиво, и система (1) несовместна.Таким образом, для любой совместной системы числа ,…, в системе (2) равны нулю. В этом случае последние уравнений в системе являются тождествами и их можно не принимать во внимание при решении системы (1). Переход от системы (1) к равносильной ей системе (2) называется прямым ходом метода Гаусса, а нахождение переменных из системы (2) – обратным ходом.Преобразования Гаусса удобно проводить, осуществляя преобразования не с самими уравнениями, а с матрицей их коэффициентов. Рассмотрим матрицу  называемую расширенной матрицей системы (1), т.к. в нее, кроме матрицы системы , дополнительно включен столбец свободных членов. |