Мех расчет. Мех.расчет ВЛ(полный)1. Механический расчет воздушных линий

• Название: Механический расчет воздушных линий
• Анкор: Мех расчет
• Дата: 20.11.2022
• Размер: 0.8 Mb.
• Имя файла: Мех.расчет ВЛ(полный)1.doc
• Тип: Реферат; #800852
• страница: 1 из 6

СОДЕРЖАНИЕ

	Введение	3
	РАЗДЕЛ 1 Механический расчет воздушных линий	3
1.1	Определение механических нагрузок	3
1.2	Уравнение состояния провода	7
1.3	Критические пролеты проводов	11
1.4	Стрела провеса	13
1.5	Выбор подвесных изоляторов	15
1.6	Выбор опор	16
1.7	Расчет тяжения опоры при обрыве в одном пролете	17
1.8	Расстановка опор по профилю с помощью шаблона	21
1.9	Прохождение ВЛ по ненаселенной и труднодоступной местности	22
1.10	Прохождение ВЛ по населенной и труднодоступной местности	22
	РАЗДЕЛ 2 Пример механического расчета воздушных линий	23
2.1	Определение механических нагрузок на провода	23
2.2	Расчет уравнения состояния провода	27
2.3	Определение стрелы провеса провода	30
2.4	Расчет и выбор изоляторов	32
2.5	Расчет тяжения провода и стрелы провеса в аварийном режиме	33
2.6	Расчет шаблона для расстановки опор на местности	35
	Приложение А	38
	Список использованных источников	45

ВВЕДЕНИЕ

Данные методические указания позволяют произвести механический расчет воздушных линий (ВЛ), который является второй частью курсового проекта по дисциплине «Электрические сети и системы». Первая часть курсового проекта «Электрический расчет ВЛ» и исходные данные на КП рассмотрены в методических указаниях № 5171[ 9].

В данных методических указаниях изложены вопросы теории механического расчета ВЛ и пример расчета. В Приложении А приведены справочные данные проводов, изоляторов и опор ВЛ, а также современные укрупненные показатели стоимости электрооборудования подстанций, включая ВЛ.
РАЗДЕЛ 1 Механический расчет воздушных линий
Механический расчет элементов ВЛ должен проводиться по методикам, изложенным в ПУЭ [1].

Механический расчет проводов и тросов ВЛ производится по методу допускаемых напряжений, расчет изоляторов и арматуры – по методу разрушающих нагрузок. По обоим методам расчеты производятся на расчетные нагрузки. Применение других методов расчета должно быть обосновано.

Элементы ВЛ рассчитываются на сочетания нагрузок, действующих в нормальных и аварийных режимах. Сочетания климатических и других факторов в различных режимах работы ВЛ ( наличие ветра, гололеда, значения температуры, количество оборванных проводов или тросов и пр.) определяются в соответствии с требованиями ПУЭ [1] .
1.1 Определение механических нагрузок
Механический расчет проводов и тросов включает в себя следующие вопросы :

1. 
   определение единичных и удельных механических нагрузок на провод;
   
2. 
   определение критических пролетов и условий появления наибольших напряжений для заданного пролета;
   
3. 
   определение напряжения в материале провода в различных расчетных режимах;
   
4. 
   определение критической температуры и наибольшей и наименьшей стрелы провеса f_нб и f_нм.
   
5. 
   определение тяжения провода при обрыве провода, определение прогиба опоры.
   

Механические нагрузки, действующие на провода и тросы ВЛ, определяются собственным весом провода, величиной ветрового напора и дополнительной нагрузкой, обусловленной гололедом. Рассчитываются единичные нагрузки, обозначаемые Р, и удельные нагрузки, обозначаемые .

Единичной называют равномерно распределенную нагрузку по длине пролета на 1м длины провода, Н/м.

Удельной называют нагрузку, которую провод длиной 1м испытывает на 1мм² своего поперечного сечения , 10⁷ Н/ м³.

Расчетные нагрузки от ветра и гололеда имеют вероятностный характер, и при их определении используются результаты статического анализа.

Единичная нагрузка, вызванная собственным весом провода Р₁ , Н/м, определится по формуле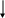

Р₁ = g  m  10^-3, (1.1)

Р₁ (₁)

где g – ускорение свободного падения, g = 9,81 м/с²;

m – погонная масса провода , кг/км, определяется по табл.1 Приложения А данного пособия .

Единичная нормативная гололедная нагрузка Р_НГ , Н/м, определится по формуле
Р_НГ =  K_i K_db_Э (d + K_i K_d b_Э) g   10^-3 , (1.2)
где K_i и K_d - коэффициенты, учитывающие изменение толщины стенки гололеда по высоте и в зависимости от диаметра провода, принимаемые по табл. 2 [пр.А];

b_Э -нормативная толщина стенки гололеда, мм, принимается по табл. 3 [пр.А] ;

d – диаметр провода, мм;

g – ускорение свободного падения , принимаемое равным 9,81 м/с²;

 - плотность льда, принимаемая 0,9 г/см³ ,[1].

Единичная расчетная гололедная нагрузка Р₂ , Н/м , определится по формуле




Р₂ = Р_НГ  _nw _p _f _d , (1.3)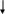




Р₂(₂₎ где Р_НГ - нормативная линейная гололедная нагрузка , Н/м;

 _nw - коэффициент надежности по ответственности, принимаемый для линий напряжением до 220кВ равным 1,0 ( для ВЛ 330-750 кВ -1,3);

_p - региональный коэффициент, принимаемый равным от 1,0 до 1,5 на основании опыта эксплуатации ;

_f - коэффициент надежности по гололедной нагрузке, равный :

1,3 для районов по гололеду I и II,[1];

1,6 для районов по гололеду I I I и выше,[1];

_d – коэффициент условий работы, равный 0,5 ,[1].

Нагрузка, обусловленная весом провода и гололедом

Р₃ = Р₁ +Р₂ (1.4)

Нормативная ветровая нагрузка на провода (тросы) Р’_НВ, Н, без гололеда определится по формуле

Р’_НВ = _W  K_l  K_W C_X W₀ F₀ sin² , (1.5)
где _W - коэффициент, учитывающий неравномерность ветрового давления по пролету ВЛ, принимаемый по табл. 4 в зависимости от ветрового давления W , [1 ];

K_l - коэффициент, учитывающий влияние длины пролета на ветровую нагрузку, принимаемый из таблицы:

Длина пролета , м	 50	100	150	 250
Коэффициент Kl	1,2	1,1	1,05	1,0

Промежуточное значение K_l определяется линейной интерполяцией.

K_W - коэффициент, учитывающий изменение ветрового давления по высоте в зависимости от типа местности и hпр, определяемый по табл.5, [пр.А ];

C_X - коэффициент лобового сопротивления, принимаемый равным:

1,1 – для проводов , свободных от гололеда, диаметром 20мм и более;

1,2 – для всех проводов и тросов, покрытых гололедом и свободных от гололеда, диаметром менее 20мм;

W₀ – нормативное ветровое давление, соответствующее 10-минутному интервалу осреднения скорости ветра (₀), на высоте 10м над поверхностью земли и принимаемый в соответствии с картой районирования территории России по ветровому давлению, принимается по табл.6, Па [пр.А];

F₀ - площадь продольного диаметрального сечения провода, м² ;

 - угол между направлением ветра и осью ВЛ(ветер следует принимать направленным под углом 90 к оси ВЛ).

Ветровое давление на провода определяется по высоте расположения приведенного центра тяжести всех проводов.

Поскольку на данном этапе расчетов еще не определена стрела провеса провода и профиль трассы, то можно принять ориентировочно в качестве h_ср нормативное расстояние до нижней траверсы , табл.7[пр.А] .

Площадь продольного диаметрального сечения провода без гололеда F₀, м², определяется по формуле

F₀ = d  L  10^-3 , (1.6)

где d – диаметр провода, мм;

L - длина пролета, м.

Единичная нормативная ветровая нагрузка на провода (тросы) Р_НВ, Н/м, без гололеда определится по формуле

Р_НВ = Р’_НВ / L

Нормативная ветровая нагрузка на провода (тросы) Р’_НВГ, Н, с гололедом определится по формуле

Р’_НВГ = _W  K_l  K_W C_X W_Г F_Г sin² , (1.7)
где C_X - коэффициент лобового сопротивления, принимаемый равным 1,2 ;

W_Г - нормативное ветровое давление при гололеде с повторяемостью один раз в 25лет, принимается W_Г = 0,25 W₀ ;

F_Г - площадь продольного диаметрального сечения провода, м² (при гололеде с учетом условной толщины стенки гололеда b_у );

Площадь продольного диаметрального сечения провода Fг, м² , определяется по формуле

Fг = ( d + 2K_i K_d b_У ) L  10^-3 , (1.8)

где d – диаметр провода, мм;

K_i и K_d - коэффициенты, учитывающие изменение толщины стенки гололеда по высоте и в зависимости от диаметра провода, определяются по табл. 2[пр.А];

b_У - условная толщина стенки гололеда , мм, принимается равной нормативной толщине b_Э по табл. 3[пр.А];

Единичная нормативная ветровая нагрузка на провода (тросы) Р_НВГ, Н/м, с гололедом определится по формуле

Р_НВГ = Р’_НВГ / L

Единичная расчетная ветровая нагрузка на провода (тросы) без гололеда Р₄ , Н/м, определится по формуле

Р₄ = Р_НВ _Н  _Р  _f , (1.9)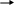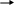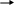

Р₄ (₄)

где Р_НВ – единичная нормативная ветровая нагрузка, Н/м;

_Н - коэффициент надежности, принимаемый равным :

1,0 – для ВЛ до 220кВ; 1,1 - для ВЛ 330-750 кВ;

_Р - региональный коэффициент, принимаемый от 1,0 до 1,3 на основании опыта эксплуатации;

_f - коэффициент надежности по ветровой нагрузке, равный 1,1.

Единичная расчетная ветровая нагрузка на провода (тросы) с гололедом Р₅ , Н/м, определится по формуле

Р₅ = Р_НВГ _Н  _Р  _f , (1.10)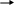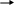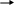

Р₅(₅)

где Р_НВГ – единичная нормативная ветровая нагрузка, Н/м;

Единичная нагрузка, определяемая весом провода без гололеда и ветром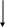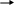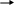

Р₄ _________

Р₆ =  Р₁² + Р₄ ² (1.11)

Р₁ Р₆

Единичная нагрузка, определяемая весом провода с гололедом и ветром

_________

Р₅ Р₇ =  Р₃² + Р₅ ² (1.12)
Р₃ Р₇

Определяем удельные нагрузки по формуле

 = Р / F , (1.13)

где Р – единичная нагрузка , Н/м;

F –расчетное сечение провода ( суммарное алюминий и сталь) , мм² .

Результаты расчетов по формулам сводим в таблицу 1.1.

Таблица 1.1

	Р1	Р2	Р3	Р4	Р5	Р6	Р7
Р, Н/м
, 107 Н/м3

1.2 Уравнение состояния провода

Провод, закрепленный в двух точках на одинаковой высоте и испытывающий равномерно распределенную нагрузку, можно рассматривать как гибкую нить, принявшую форму цепной линии. Напряжение в любой точке такой нити будет

обусловлено только растяжением и направлено по касательной к кривой (рис.1.1)
А Б

f

Н Н

h





L

Рисунок 1.1

1. 
   Расстояние по горизонтали между точками подвеса А и Б называется пролетом(L) .
   
2. 
   Расстояние по вертикали в середине пролета между проводом и прямой АБ, соединяющей точки провеса, называется стрелой провеса ( f ).
   
3. 
   Сила, действующая в любой точке провода, называется тяжением ( Т). Тяжение в низшей точке кривой провисания, направленное горизонтально, обозначается буквой Н .
   
4. 
   Сила, действующая на единицу сечения провода, называется напряжением (  ).
   

Тяжение по проводу при любых условиях работы и в каждой его точке направлено по касательной к кривой провисания провода и определяется выражением

Т =  F, (1.14)

где F – полное поперечное сечение провода, мм²;

 - напряжение , Н/ мм² .

При закреплении в натяжных гирляндах на опорах анкерного типа тяжение провода передается на опоры, вызывая в опорах силу, равную по величине, но противоположную по направлению; эта сила называется реакцией.

Напряжение не должно превосходить допускаемое 1. Напряжение в точках крепления А и Б не должно превосходить 105% допускаемого напряжения для алюминиевых и 110% для сталеалюминевых проводов.

При равной высоте точек подвеса

_А = _Б = о +   , (1.15)

где о - напряжение в низшей точке провисания провода, Н/ мм² ;

 - стрела провеса провода при удельной нагрузке , м.

Комбинированные, в том числе сталеалюминевые провода, рассчитываются по полному тяжению, действующему по проводу, по суммарному сечению алюминиевой и стальной части, по модулю упругости, температурному коэффициенту линейного расширения и допускаемому напряжению провода в целом 1.

При расчете проводов следует принимать такие сочетания климатических условий, которые дают наиболее невыгодные по механическим нагрузкам значения напряжения в проводе в одних случаях и максимальные величины стрел его провеса в других случаях.

Расчет ВЛ по нормальному режиму работы необходимо производить для сочетания следующих условий :

1. 
   Высшая температура t₊ , ветер и гололед отсутствуют (формула 1.1).
   
2. 
   Низшая температура t _ , ветер и гололед отсутствуют ( формула 1.).
   
3. 
   Среднегодовая температура t _сг , ветер и гололед отсутствуют (формула 1.1).
   
4. 
   Провода и тросы покрыты гололедом ( формула 1.3) , температура при гололеде минус 5С, ветер отсутствует.
   
5. 
   Ветер ( формула 1.9), температура при W0 минус 5С , гололед отсутствует.
   
6. 
   Провода и тросы покрыты гололедом , ветер при гололеде на провода (формула 1.10), температура при гололеде минус5С.
   
7. 
   Расчетная нагрузка от тяжения проводов определяется при расчетных ветровых (формула 1.10) и гололедных (формула 1.3) нагрузках, умноженных на коэффициент надежности по нагрузке от тяжения (_f = 1,0 …1,3 ).
   

Расчет ВЛ по аварийному режиму необходимо производить для сочетания следующих условий :

1. 
   Низшая температура t _ , ветер и гололед отсутствуют (формула 1.1).
   
2. 
   Среднегодовая температура t _сг , ветер и гололед отсутствуют (формула 1.1).
   
3. 
   Провода и тросы покрыты гололедом (формула 1.3) , температура при гололеде минус 5С, ветер отсутствует.
   
4. 
   Расчетная нагрузка от тяжения проводов определяется при расчетных ветровых (формула 10) и гололедных (формула 1.3) нагрузках, умноженных на коэффициент надежности по нагрузке от тяжения (_f = 1,0 …1,3 ).
   

Для решения этих задач зависимость напряжений от нагрузки и температуры выражают в виде уравнения, которое называется уравнением состояния провода.

Для вывода уравнения состояния рассмотрим провод в изолированном анкерном пролете с точками подвеса на одной высоте. Для начального состояния введем следующие обозначения :

L₀ - длина пролета, м; ₀ – удельная нагрузка, Н/(м  мм²) ; t₀ – температура окружающей среды,  С; ₀ – напряжение в низшей точке провода, Н/ мм² .

Для искомого состояния примем те же обозначения, но без индексов.

В результате алгебраических преобразований с учетом относительного упругого удлинения провода получим уравнение состояния в виде

² L² Е ₀² L² Е

 - ----------- = ₀ - -------------- - Е (t - t₀ ), (1.16)

24² 24₀²

где Е – модуль упругости материала провода , Па ,(10³ Н/мм²), табл. 8,[ пр.А ];

 - температурный коэффициент линейного расширения, 10 ^–6 º С^-1, табл.8, [пр.А ].

С помощью этого уравнения можно найти напряжения в проводе в любых требуемых условиях на основании известных напряжений, нагрузок и температур в начальном состоянии. При подстановке отрицательных температур необходимо строго соблюдать правило знаков.

В общем случае уравнение состояния можно представить в виде кубического уравнения

²( + А) = В, (1.17)

где А и В – коэффициенты кубического уравнения.
₀²Е  l² ²Е  l²

А = - _{0 +} -------------- + Е ( t - t₀ ) В = -----------

24₀² 24
Во всех режимах напряжения должны быть меньше допустимых.

ПУЭ устанавливают допустимое напряжение в материале _доп в процентах от предела прочности [1 ].

_доп = _в /100,

где _В – временное сопротивление (предел прочности), т.е. такое напряжение, при котором провод разрывается, Н/мм² [ 1].

Эти значения различны для режимов наибольшей нагрузки, наименьшей температуры и среднегодовой температуры.

Предел прочности по растяжению _В может быть найден по выражению

_В = R / F , (1.18)

где R – разрывное усилие провода, Н, табл.1, [пр.А ];

F – расчетное сечение провода, мм².

По ПУЭ допускаемое напряжение в проводах рассчитывается для нормального и аварийного режимов .

Выбор допускаемого напряжения провода производится на основе определения критических пролетов.

3. 
   Критические пролеты проводов
   

При ограничении допускаемых напряжений для трех режимов возникает вопрос, какой из этих режимов следует принимать в качестве исходного. Этот вопрос решается путем вычисления так называемых критических пролетов для различных режимов.

Критический пролет в общем виде определяется по формуле

_______________________

4 _n 1,5[( _{n -}  _m) + (t _n - t _m )]

l_к = _------  -------------------------------------- (1.19 )

_m (_n /_m)² - (_д /  _m ) ²
где  = Е^-1 – коэффициент упругого удлинения провода, мм² / Н.

Различают три критических пролета :

1. 
   l_к1 - это пролет такой длины, для которого напряжение провода в режиме среднегодовых температур равно допустимому _э, а в режиме низшей температуры равно допустимому  _{_,} т.е определяет переход от расчетных условий при низшей температуре к среднегодовым условиям. При этом
   

_n = ₁ ; t _n = t _э ;  _n = _{э ;} _m = ₁; t _m = t _{_};  _m =  _{_}

2. 
   l_к2 - имеет место в том случае, когда в режиме максимальных внешних нагрузок в режиме низшей температуры напряжение в проводе равны допустимым _г, т.е. определяет переход от расчетных условий при низшей температуре к условиям наибольшей нагрузки. При этом
   

_n = ₇ ; t _n = t _г ;  _n = _{г ;} _m = ₁; t _m = t _{_};  _m =  _{_}

3) l_к3 - имеет место в том случае, когда напряжение в режиме максимальных внешних нагрузок равно допустимому _{г ,} а в режиме среднегодовых нагрузок равно допустимому _э , т.е. определяет переход от расчетных среднегодовых условий к условиям наибольшей нагрузки. При этом

_n = ₇ ; t _n = t _г ;  _n = _{г ;} _m = ₁; t _m = t _э;  _m =  _э

Для сталеалюминевых проводов критические пролеты можно определить по следующим формулам [ 8,с .60]:

________________________

4,46 _  Е (tэ - t_ ) – 0,325 _

l_1к= -----------  ------------------------------------- (1.20)

₁ Е


________________________

4,9 _г  Е (t_г - t_ ) + 0,119 _г

l_2к= -----------  ------------------------------------- (1.21)

₁ Е (₇ / ₁)² – 1,29


________________________

4,9 _г  Е (t_г - t_Э ) + 0,405 _г

l_3к= -----------  ------------------------------------- (1.22)

₁ Е (₇ / ₁)² – 2,82


где _ - допускаемое напряжение при низшей температуре, Н/мм² , табл.9 [пр.А];

_г - допускаемое напряжение при наибольшей нагрузке, Н/мм²,табл.9 [пр.А];

_э – допускаемое напряжение при среднегодовой температуре, Н/мм² ,табл.9 [пр.А].

Полученные значения длин критических пролетов следует сравнить с действительной величиной пролета и сделать выводы. Рекомендуется в первую очередь определить l_к2и сравнить его с действительным пролетом.

Далее могут возникнуть следующие случаи :

1. 
   Если l_к1<l_к2< l_к3 ,то расчетным пролетом является l_к1;l_к3 .
   
2. 
   Если l_к1 l_к2l_к3 ,то расчетным пролетом является l_к2.
   
3. 
   Если l_к1 – мнимый , l_к2<l_к3 ,то расчетным пролетом является l_к3.
   
4. 
   Если l_к3 – мнимый , то расчетным пролетом является l_к1.
   

После определения критических пролетов необходимо рассчитать уравнения состояния и определить значения напряжений в проводе в различных режимах .

Если 1 случай, то уравнение состояния для расчета провода с учетом критических пролетов будет иметь следующий вид при соотношении фактического и критического пролетов :

1) Если l> l_к3

² L² Е _г² L² Е

 - ----------- = _г - -------------- - Е ( t - t_г ), (1.23)

24² 24_г²
2) Если l< l_к1

² L² Е ₁² L² Е

 - ----------- = __{_} - -------------- - Е ( t - t__{_} ), (1.24)

24² 24__{_}²
3) Если l_к1<l_к3

² L² Е ₁² L² Е

 - ----------- = _э - -------------- - Е ( t - t_э ), (1.25)

24² 24_э²
Если 2 случай, то уравнение состояния для расчета провода с учетом критических пролетов будет иметь следующий вид при соотношении фактического и критического пролетов :

-при l< l_к2 – уравнение (1.24)

-при l >l_к2 – уравнение (1.23)

Если 3 случай, то уравнение состояния для расчета провода с учетом критических пролетов будет иметь следующий вид при соотношении фактического и критического пролетов :

-при l< l_к3 – уравнение (1.25)

-при l >l_к3 – уравнение (1.23)

Если 4 случай, то уравнение состояния для расчета провода с учетом критических пролетов будет иметь следующий вид при соотношении фактического и критического пролетов :

-при l< l_к1 – уравнение (1.24)

-при l >l_к1 – уравнение 1.(25)

Расчет проводится для режимов :

1. 
   Максимальных температур (t =t+;  = 1).
   
2. 
   Минимальных температур (t =t-;  = 1).
   
3. 
   Среднегодовых температур (t =tэ;  = 1).
   
4. 
   Гололеда (t =tг;  = 3).
   
5. 
   Режима максимальных нагрузок (t =tг;  = 7).
   

Соотношения , определяющие исходные условия для расчета проводов сводим в таблицу 1.2.

Таблица 1.2

Случай	Соотношение пролетов	Исходные напряжения	Расчетный критический пролет	Формулы
1	lк1< lк2< lк3	_,э, г	lк1 иlк3	l> lк3 (1.23) l< lк1 (1.24) lк1<l<lк3 (1.25)
2	lк1 lк2lк3	_, г	lк2	l< lк2 (1.24) l >lк2 (1.23)
3	lк1 – мнимый , lк2 < lк3	э, г	lк3	l< lк3 (1.25) l >lк3 (1.23)
4	lк3 – мнимый lк1 < lк2	_,э,	lк1	l< lк1 (1.24) l >lк1 (1.25)

1.4 Стрела провеса

Одной из величин, определяющих высоту опор, является стрела провеса. При достаточно больших отношениях длины пролета L к стреле провеса f (что соответствует действительности) кривая провеса провода очень близка к параболе вида y = h + kx² . При совмещении начала координат с низшей точкой провеса (h =0) уравнение параболы примет вид y = kx² . В отечественной практике расчеты проводов производятся по параболе; исключением являются расчеты проводов с очень большими пролетами (800-1000 м).

Исходя из этого уравнения и полагая, что длина провода примерно равна длине пролета l  L , при одинаковой высоте точек подвеса стрела провеса определится (при пролете до 600 м)

  L²

f = --------- (1.26)

8  ,
где - удельная нагрузка при конкретных климатических условиях, Н/ м мм²;

 - напряжение при растяжении в низшей точке провода, Н /мм².

Максимальная стрела провеса f_нб может возникнуть только при отсутствии ветра при условии:

1. 
   при гололеде, когда провод испытывает наибольшую вертикальную нагрузку (₃);
   

f_нб = f₃ = ₃ l ² / 8 ₃ (1.27)

2. 
   при наивысшей температуре воздуха, когда провод испытывает вертикальную нагрузку только от собственной массы (₁).
   

f_нб = f₁ = ₁l² / 8 ₊ (1.28)
Температура, при которой стрелы провеса равны f₃ = f₁, называется критической температурой

_г(1 - ₁ / ₃ )

t_К = t_г + --------------------- (1.29)

 Е
Если t₊  t_К, то f_нб = f₁ (1.30)

Если t₊  t_К, то f_нб = f₃ (1.31)
Длина провода в пролете Lпр, м, определится как длина дуги параболы, (погрешность составляет 0,1%)

8 f ² ²L³

Lпр = L + ------- = L + ------------- (1.32)

3L 24²

Наименьшая стрела провеса будет при минимальных температурах , но без гололеда

 ₁L²

fнм = --------- (1.33)

8  _ ,

Кривые строятся в координатах L, h , за начало координат принимается точка с координатами L /2 и h = h_ТР - г - fнб (fнм).

Масштаб по горизонтали и вертикали может быть разным.
1.5 Выбор подвесных изоляторов

Выбор типа и материала изоляторов производится на основании требований ПУЭ с учетом климатических условий и условий загрязнения [1, п.2.5.98 ].

На ВЛ 35- 220кВ рекомендуется применять стеклянные или полимерные изоляторы. Выбор количества изоляторов в гирляндах производится в соответствии с [1,гл.1.9].

Изоляторы и арматура выбираются по нагрузкам в нормальных и аварийных режимах ВЛ с учетом климатических условий. Расчетные усилия в изоляторах и арматуре не должны превышать значений разрушающих нагрузок (механической или электромеханической), установленных техническими условиями, деленных на коэффициент надежности по материалу _М. :

1. 
   в нормальном режиме
   
   • 
     при максимальных нагрузках _М = 2,5;
     
   • 
     при эксплуатационных нагрузках для поддерживающих гирлянд _М = 5,0;
     
   • 
     для натяжных гирлянд _М = 6,0.
     
2. 
   в аварийном режиме (для напряжения 330кВ и меньше) _М = 1,8.
   

Расчетный коэффициент надежности по материалу определится
 = Рразр / Ррасч  _М (1.34 )
где Рразр – допустимая разрушающая нагрузка, Н;

Ррасч - расчетная разрушающая нагрузка, Н.
Порядок расчета :

1. 
   Выбираем тип и число изоляторов в соответствии с условиями окружающей среды [пр.А, табл. 11 ].
   

2) Определяем строительную высоту изолятора из, разрушающую нагрузку Рразр, массу изолятора mиз [пр.А, табл. 12 ].

3. 
   Определяем длину гирлянды изоляторов г, м
   

г = n  из, (1.35)

где n – число изоляторов;

из - строительная высота изолятора, см.

3. 
   Определяем нагрузку, действующую на гирлянду изоляторов. Она состоит из веса гирлянды и веса провода. Расчет производим для двух режимов (без ветра и гололеда Р₁ и с ветром и гололедом Р₇) и выбираем максимальную нагрузку.
   

Р_{1(7 )} расч = К ₁₍₇₎  (Р_{1(7 )}  Lвес + Gг), (1.36)

где К ₁₍₇₎ - нормативный коэффициент запаса :

К₁ = 5 (режим без ветра и гололеда);

К₇ = 2,5 (режим с ветром и гололедом) ;

L вес - весовой пролет, т.е. расстояние между низшими точками кривых провисания в пролетах, примыкающих к рассматриваемой опоре, м.

L вес = 1,25 L (рис1.2)









L вес
Рисунок 1.2
Gг - вес гирлянды изоляторов, H.

Gг = n  m_из  g, (1.37)
где m_из – масса изолятора, кг;

g – ускорение свободного падения, g = 9,81 м/c².
5) Определяем коэффициент надежности по материалу  для режима с наибольшей расчетной нагрузкой, полученное значение сравниваем с нормативным _М = 1,8 [1].

3. 
   Минимально допустимое расположение траверсы опоры определится
   

h_ТР = h_Г + fнб + г , (1.38)

где h_Г - габарит линии ,т. е. минимальное расстояние от провода до земли ,м [1, т.2.5.20, 2.5.22 ].

3. 
   По табл. 9 уточняем тип опоры [9,с.383].
   

6. 
   Выбор опор
   

Опоры, фундаменты и основания ВЛ должны рассчитываться на сочетание расчетных нагрузок нормальных режимов по первой и второй группам предельных состояний:

Первая группа включает предельные состояния, которые ведут к потере несущей способности элементов или к полной их непригодности к эксплуатации, т.е к их разрушению. К той группе относятся состояния при наибольших внешних нагрузках и при низшей температуре.

Вторая группа включает предельные состояния, при которых возникают недопустимые деформации, перемещения или отклонения элементов, нарушающие нормальную эксплуатацию, к этой группе относятся состояния при наибольших погибах опор.

Нагрузки, воздействующие на строительные конструкции ВЛ, в зависимости от продолжительности воздействия подразделяются на постоянные и временные

( длительные, кратковременные, особые).

К постоянным относятся - собственный вес провода, строительных конструкций, гирлянд изоляторов, тяжение проводов и тросов при среднегодовой температуре и отсутствии ветра и гололеда.

К длительным нагрузкам относятся нагрузки, создаваемые воздействием неравномерных деформаций оснований, не сопровождающихся изменением структуры грунта.

К кратковременным нагрузкам относятся – давление ветра на провода с гололедом и без, вес гололеда, тяжение проводов и торосов сверх их значений при среднегодовой температуре и т.д.

К особым нагрузкам относятся нагрузки, возникающие при обрыве проводов или тросов, а также нагрузки при сейсмических воздействиях.

Опоры могут быть жесткими (металлические) и гибкими (деревянные).У жестких опор при обрыве провода из-за неравномерного тяжения слева и справа будет отклоняться только гирлянда. У гибких опор наблюдается прогиб опоры (опора отклоняется в ту же сторону, что и гирлянда).

Этот факт влияет на величину стрелы провеса и его надо учитывать при выборе опор.