23a Степени свободы — это совокупность независимых координат перемещения и/или вращения, полностью определяющая положение системы или тела.
Числа степеней свободы-это число независимых переменных (координат), которые полностью определяют положение системы в пространстве.
|
23б Эне́ргия — скалярная физическая величина, являющаяся единой мерой различных форм движения и взаимодействия материи, мерой перехода движения материи из одних форм в другие.
Вну́тренняя эне́ргия тела (или U) — это сумма энергий молекулярных взаимодействий и тепловых движений молекул. Внутренняя энергия является однозначной функцией состояния системы.
Коли́чество теплоты́ — энергия, кот. получает или теряет тело при теплопередаче. Количество теплоты является одной из основных термодинамических величин.
|
24а В люб.изолирован.с-ме запас энергии остаётся постоянным. (Джоуль) Кол-во теплоты, полученное с-мой, идёт на изменение её внутренней энергии и совершение A против внешних сил.Изменение внутр.энергии с-мы при переходе её из одного состояния в др.= сумме А внешних сил и кол-ва теплотыQ, переданного с-ме, то есть, оно зависит только от нач. и конечн. состояния с-мы и не зависит от способа переходa. В циклическом процессе внутр.энергия не измен.  =0Изменен.полной энергии с-мы в квазистатичес.процессе= кол-ву Q, сообщён.с-ме, в сумме с изменением энергии,кол-вом в-ва N при хим.потенциале μ, и A’, совершён.над с-мой внешн.силами и полями,за вычетом А , совершён.самой с-мой против внешних сил =0Изменен.полной энергии с-мы в квазистатичес.процессе= кол-ву Q, сообщён.с-ме, в сумме с изменением энергии,кол-вом в-ва N при хим.потенциале μ, и A’, совершён.над с-мой внешн.силами и полями,за вычетом А , совершён.самой с-мой против внешних сил
∆U=Q-A+μ∆N+A’
|
24б. Если газ, расширяясь, пере�двигает поршень на бесконечно малое расстояние dl, то производит над ним работу:δА=Fdl=pSdl=pdV, где S— площадь поршня, Sdl=dV— изменение объема системы. δA=pdV.ПолнуюА, совершаемую газом при изменении его объема от V1 до V2:A=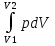 . .
|
25аТеплоёмкостьидеального газа — отношение количества теплоты, сообщённого газу, к изменению температуры δТ, которое при этом произошло.
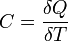
|
25б Термическим коэффициентом давления-изменение давления в зависимости от изменения температуры в-ва. β= )v, )v,
где(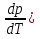 v– частная производная,характеризующая изменения давления p,если температура вещества повышается на один градус, а объем остается постоянным, давление p является функцией температуры. v– частная производная,характеризующая изменения давления p,если температура вещества повышается на один градус, а объем остается постоянным, давление p является функцией температуры.
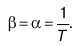
|
26a 1з.термодин-Изменение полной энергии с-мы в квазистатическом процессе=кол-ву теплоты Q, сообщенного с-ме, в сумме с изменением энергии, связанной с кол-вом вещества N при хим.потенциале μ, и работы A', совершённой над с-мой внешними силами и полями, за вычетом работы А, совершённой самой с-мой против внешних сил» :∆U=Q-A+μ∆N+A’
Для элементарного кол-ва теплоты δQ, элементарной работы δA и малого приращения dU внутренней энергии 13.термодинамики имеет вид:dU=ΔQ-∆A+μdN+δA
Разделение работы на 2 части, одна описывает работу, совершённую над системой, а вторая – работу, совершённую самой системой.
Приращение теплоты часто выражают через температуру и приращение энтропии:δQ=Tds .
|
26б
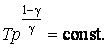 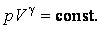
|
27аКривая на термодинамических диаграммах, изображающая П. п.-политропа. Простейшим примером обратимого П. п. может служить П.п. с идеальным газом, определяемый уравнением pV n = const, n=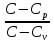 показатель политропы (Cp и Cv — теплоёмкости газа ). у-е политропы в ином виде: pT^ показатель политропы (Cp и Cv — теплоёмкости газа ). у-е политропы в ином виде: pT^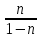 =const илиVT =const илиVT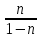 = const. у-е П. п. идеального газа включает частные случаи у-я: адиабаты С =0, n = Cp/Cv, , изобары (С = Ср, n = 0), изохоры (С = Cv, n = ¥) и изотермы (С = ¥, n = 1). Работа А идеального газа в П. п. против внешнего давления A= = const. у-е П. п. идеального газа включает частные случаи у-я: адиабаты С =0, n = Cp/Cv, , изобары (С = Ср, n = 0), изохоры (С = Cv, n = ¥) и изотермы (С = ¥, n = 1). Работа А идеального газа в П. п. против внешнего давления A=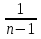 (p1V1-p2V2) (p1V1-p2V2)
|
27б Распределение Ма́ксвелла — распред. вероятности,лежит в основ.кинетич.теории газов,кот.объясняет многие фундаментальные св-ва газов(давление и диффузию).Применимо для электронных процессов переноса и др.явлений, применимо к множеству св-в индивид.м-кул в газе.Считают его распред.энергий м-кул в газе,но может также применяться к распред.скоростей ,импульсов и модуля импульсов м-кул.Также оно выражено как дискретное распределение по множеству дискретных у-й энергии или как непрерывное распред.по некот. континууму энергии.Выражено как дискретное распределение энергии: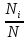 = =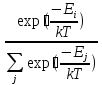
|
28а![p=p_0\exp\left[-mg\frac{h-h_0}{rt}\right],](24556_html_m3cac6617.png)
|
28бРаспред.Больцмана-распред.вероятностей различн.энергетич.состояний идеальной термодин.с-мы в ус-виях термодин.равновесия.
Pаспред.Больц.ср.число частиц с полной энергией Ei (<ni>=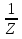 e-Ei/kвТNi) e-Ei/kвТNi)
Постоянная Z находится из условия, что сумма ni по всем возможным значениям i= заданному полному числу частиц n в системе: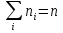
Kогда движение частиц подчиняется класс.механике, энергию Ei можно считать состоящей из кинет.энергииEi1=Ei(кин) частицы,
внутренней энергииEI2=Ei(вн) и
потенциальной энергииEi3=Ei(пот) во внешнем поле, зависящей от положения частицы в пр-ве: Ei=Ei1+Ei2+Ei3
|
29aПодъёмная сила — составляющая полной аэродинамической силы,ḻ вектору скорости движ.тела в потоке жидк. или газа, возникающая в результате несимметричности обтекания тела потоком. В соответствии с з.Бернулли, статическое давление среды в тех областях, где скорость потока более высока, будет ниже, и наоборот. Y+P=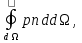 где:Y — это подъёмная сила,P — это тяга, где:Y — это подъёмная сила,P — это тяга,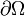 — граница профиля,p — величина давления,n — нормаль к профилю — граница профиля,p — величина давления,n — нормаль к профилю
|
29б Обратимыми называют процессы, в результате совершения которых в прямом и обратном направлениях термодинамическая система возвращается в исходное состояние; таким образом, совокупность прямого и обратного процессов не вызывает в окружающей среде никаких изменений.Необратимыми называют процессы, при проведении которых в прямом и затем в обратном направлении система не возвращается в исходное состояние. Из повседневной практики известно, что все естественные самопроизвольные процессы, происходящие в природе, являются необратимыми; обратимых процессов в природе не существует.
|
30а Тепловая машина состоит из нагревателя, раб.тела и охладителя раб.тела.Охладитель-окружающая среда.Тепловая машина работает по принципу замкнутого цикла, совершая круговой процесс.Согласно1 з.термодинамики,это тепло расходуется на нагревание рабочего тела и на совершение механ.работыQ1= E2� E1+ A13 При обратном цикле над газом производится работа: газ сжимается и передает охладителю кол-во.тепла� Q2= E1� E2+ A31, т.е. Q1� Q2= A13+ A31=A.Отношение полезной работы, совершенной машиной, к кол-ву полученного тепла составляет КПД тепловой машины ὴ=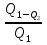 = =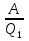 Понятно, что КПД машины всегда меньше единицы, поскольку не все кол-во полученного тепла переходит в полезную работу. Понятно, что КПД машины всегда меньше единицы, поскольку не все кол-во полученного тепла переходит в полезную работу.
|
30б Цикл Карно состоит из последовательных расширения и сжатия газа, причем каждый из процессов совершается сначала изотермически, а затем адиабатически. При прямом цикле тело по-прежнему сначала получает тепло, а затем отдает его. Достоинство цикла Карно состоит в том, что все процессы обратимы, и, следовательно, КПД такой машины будет максимальным.
|
31а 2 начало термодинамики формулировки:
1)Невозможен вечный двигатель второго рода
2)Невозможен процесс, единственным конечным результатом которого является превращение всей теплоты, полученной от нагревателя, в эквивалентную ей работу
3)Коэффициент полезного действия тепловой машины всегда строго меньше единицы: ɳ<1
4)Без совершения работы нельзя отбирать теплоту от менее нагретого тела и отдавать более нагретому
5)При любых процессах, происходящих в замкнутой системе, ее энтропия S не может убывать: ΔS≥Ο, где знак равенства относится к обратимым, а неравенства – к необратимым процессам.
|
31б Величина S = Q/T, или приведенная теплота, была названа энтропией. Эта величина является функцией состояния термодинамической системы.Изолированные(замкнутые)системы не обмениваются веществом и энергией с окружающим пространством. В таких системах изменение энтропии ΔS = 0 (для обратимых процессов) и ΔS >0 (для необратимых). Все реальные процессы необратимые и поэтому энтропия в изолированной системе для самопроизвольных процессов может только возрастать, что указывает на однонаправленность всех процессов в природе. Этот вывод получил названиезакона возрастания энтропии.
|
32а Математ.выражение2 з.термодинамики для обратимых процессов dq=Tds, q=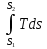 . .
где q – подводимая (извне) или отводимая от рабочего тела теплота;
s, Дж/(кг.К) – удельная энтропия, являющаяся параметром состояния
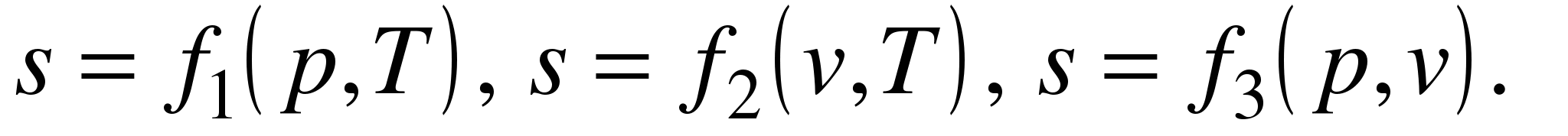
Математическое выражение второго закона термодинамики для необратимых процессов:
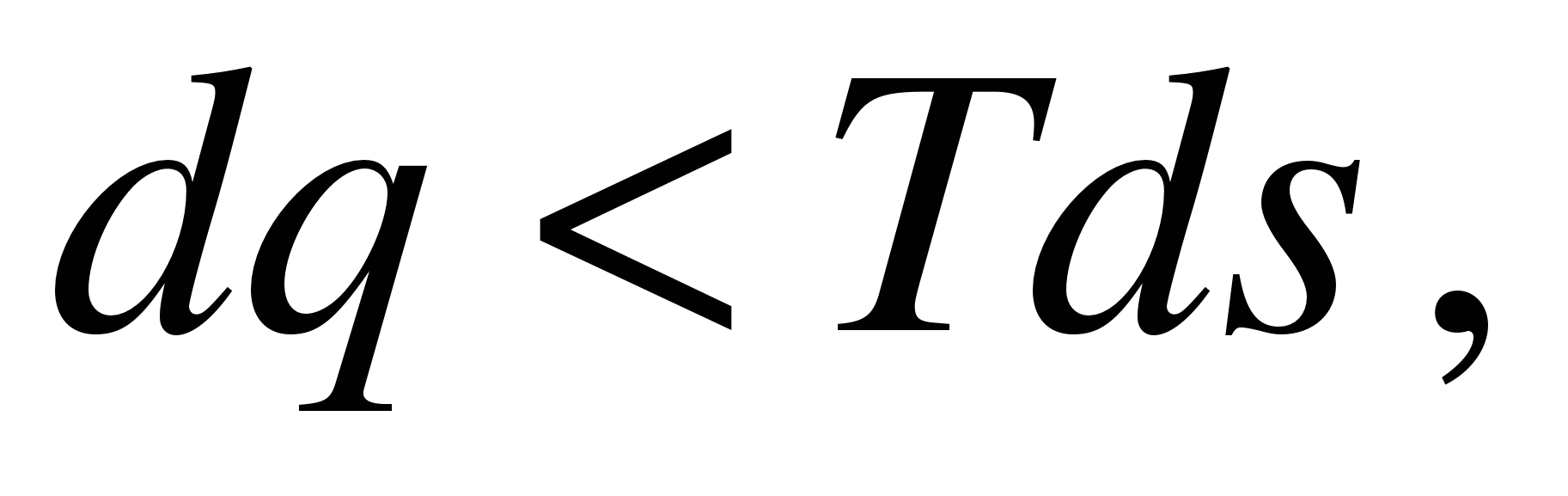
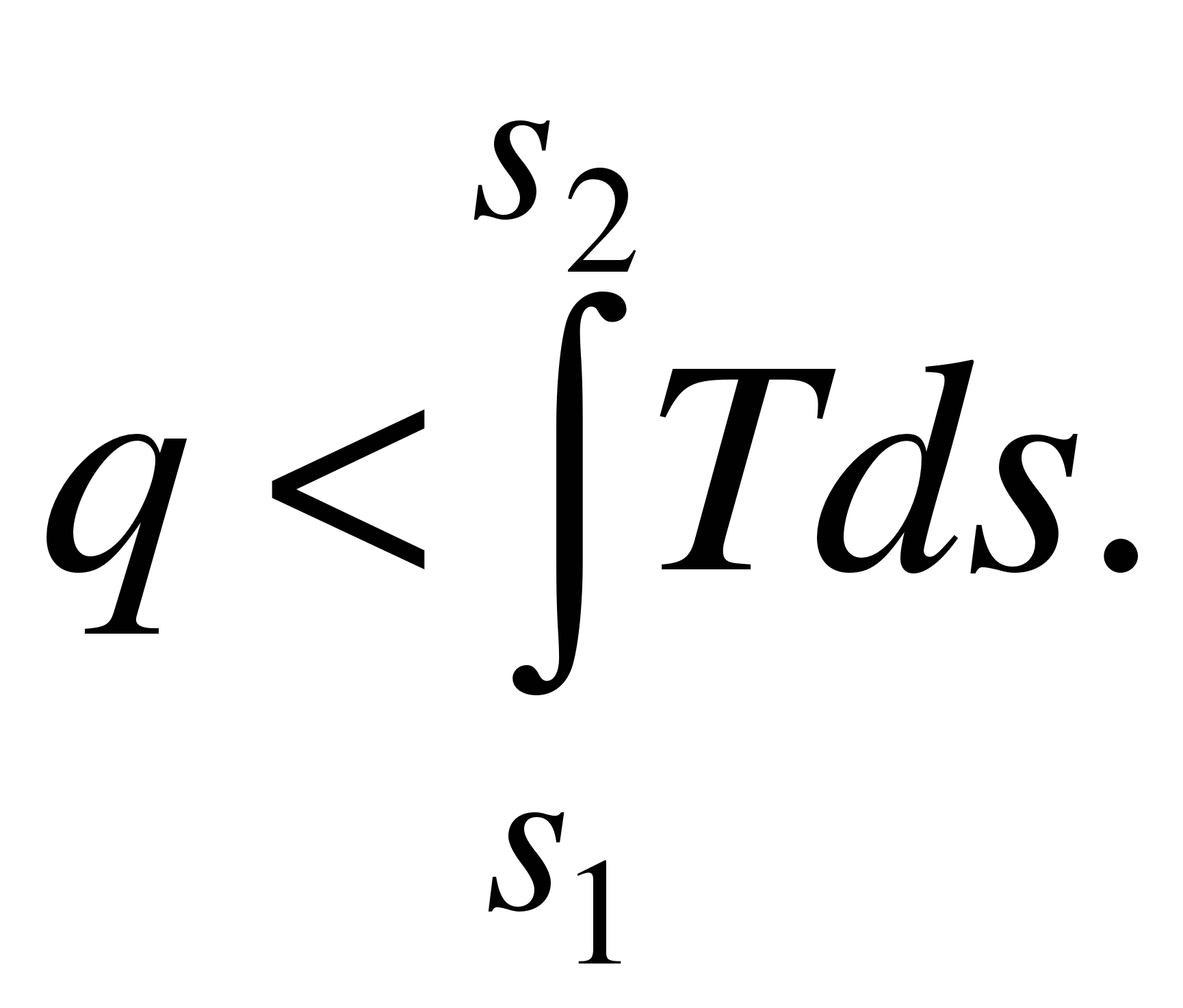
|
32б Понятия энтропии было дано Больцманом. Для этого было введено понятие термодинам. вероятности(W)данного состояния некоторой с-мы -число возможных неотличимых микроскопических состояний с-мы реализующ.определенное макроскоп. состояние этой с-мы(или число перестановок одноименных элементов,при кот.сохран.данное макросост). Термод. вероятность-макс,когда с-ма наход.в равновесном состоянии.Энтропия-вероятностная статист.величина.Ее увелич.вероятно,но не исключ.флуактации.На этой основе Клаузиус 1867гвыдвинул гипот.о теплов.смерти Вселенной. Больцман опроверг гипотезу и показал,что з.возраст.энтропии-статист. закон,т.е.возможны отклонения.Энтропия замкн.с-мы макс.при достижении с-мой равновесного состояния.
| |
 Скачать 230.67 Kb.
Скачать 230.67 Kb.