Навигация по странице: =<
|
Шпоры физика(2 семестр ). Механическое движение изменение положения тела относительно других тел. Скорость
33а По изменен.энтропии можно судить об обратим.или необратим.процессов,протек.в замкн.с-ме:чем меньше ΔS, тем ближе процесс к обратим.Энтропия-величина,с помощью кот.учит. потери теплоты,происход.в реальных процессах, превращение теплоты в др.виды энергии. Yвелич.энтропии ΔS при каком-либо процессе показывает, что часть теплоты, содержащейся в с-ме=TΔS,не может быть превращ.в работу,т.к. будет рассеяна между окружающ.телами.S–величина аддитивная.значит,что S сложн.с-мы=сумме энтропий подсистем, т. е. S=S1+S2+...+Sn В современ.термодин.рассм. процессы, происход.не только в замкн.с-мах.Для хар-ки этих процессов также вычисл.изменениеS ,но если с-ма обменивается теплотой с внешн. средой,то ее∆Sможет вести себя любым образом.
|
33б 3 НАЧАЛО ТЕРМОДИН. (Нернста теорема) - устанавливает, что энтропия физической системы при стремлении температуры к абсолютному нулю не зависит от параметров системы и остается неизменной. М. Планк дополнил теорему Нернста гипотезой, что энтропиявсех тел при абсолютном нуле температуры равна нулю. Из третьего начала термодинамики вытекают важные следствия о свойствах веществ вблизи абсолютного нуля. Так, обращаются в нуль: удельные теплоемкости при постоянном объеме (Сv) и при постоянном давлении (Сp), термический коэффициент расширения и давления. Из третьего начала термодинамики следует также недостижимость абсолютного нуля температуры при конечной последовательности термодинамических процессов.
|
34а Реальн.газ-газ,кот.неописыв.у-ем состояния идеальн.газа Клапейрона-Менделеева.Зависим. между его пар-ми показыв,что м-лы в реальн. газе взаимод.между собой и занимают определен. объём.Состояние реального газа часто на практик описыв.обобщённым у-ем М—К: pV=Zr(p,T)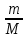 RT ,Zr = Zr (p,T)k сжимаем. газа;Межмолекул. взаимод.имеет электростатич. природу.Перв. предполож.существ.Ван-дер-Ваальс1873для объяснен.св-в реальн.газов и жидк.В наиболее широком смысле под ним можно понимать такие взаимод. между люб.частицами при кот.не происх. образован.хим,ковалент.или ме.связей.Эти взаимод. существенно слабее ковалент.и не приводят к существен.перестройке электрон. строения взаимод.частиц. RT ,Zr = Zr (p,T)k сжимаем. газа;Межмолекул. взаимод.имеет электростатич. природу.Перв. предполож.существ.Ван-дер-Ваальс1873для объяснен.св-в реальн.газов и жидк.В наиболее широком смысле под ним можно понимать такие взаимод. между люб.частицами при кот.не происх. образован.хим,ковалент.или ме.связей.Эти взаимод. существенно слабее ковалент.и не приводят к существен.перестройке электрон. строения взаимод.частиц.
|
34б Для одного моля газа Ван-дер-Ваальса оно имеет вид:
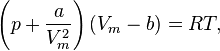 где где
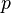 — давление, — давление,
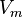 — молярный объём, — молярный объём,
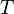 — абсолютная температура, — абсолютная температура,
|
35а Проанализируем изотермы уравнения Ван–дер–Ваальса – зависимости Р от V для реального газа при постоянной температуре. Умножив уравнение Ван-дер-Ваальса на V 2 и раскрыв скобки, получаем
PV 3 – (RT + bP) vV 2 + av2V - abv3 = 0.
|
35б Нижн—изотерм.при темп.ниже критич. участки— метастабильные состояния.
Участок левее т.F — нормал.жидкость.т.F — кипен.Прямая FG — равновесие жидк.и газообр.фазы.УчастокFA—перегретая жидк.Участок F′A — растянутая жидкость (p<0).
Участок AC — аналит.продолжение изотермы, физ. невозможен.Участок CG — переохлажд. пар. Точка G — точка росы. Участок правее точки G — нормальный газ.К — критическая изотермаK -крит.точка.верхние3— сверхкритические изотермы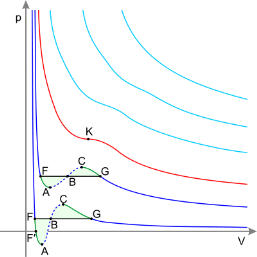
|
36а Изотермы жидкости строятся по тому же принципу, что и для газа. Дело осложняется тем, что часть температур равновесия лежит выше критической температуры азота ( 126 К), вследствие чего энтальпию жидкого азота при этих температурах снять не представляется возможным. В этом случае можно поступить следующим образом: вычислить среднюю теплоемкость жидкого азота в интервале, скажем, 110 - 120 К и считать условно, что и далее, при температурах выше критической, теплоемкость азота в смеси остается такой же.
|
36б В явлениях переноса каждая м-ла при своем хаотическом движении переносит некот. физ.величину.В случае теплопроводности переносимой величиной является кинет.энергия м-лы,кот.переносится оттуда,где она больше, туда,где она меньше,в случае вязкого трения м-ла переносит импульс.dФ=-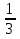 n<v><ƛ> n<v><ƛ>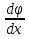 dSdt является общим уравнением переноса физической величины ϕ.Под ср.длиной свободного пробега понимают ср.расстояние,кот.проходит м-ла между 2 последовательными соударениями.За секунду м-ла в ср.проходит расстояние, численно =ее ср.скорости<v>. Если за это же время она испытает в среднемстолкновений с др. м-лами, то ее ср.длина свободного пробега <ƛ>=<v>\<v> dSdt является общим уравнением переноса физической величины ϕ.Под ср.длиной свободного пробега понимают ср.расстояние,кот.проходит м-ла между 2 последовательными соударениями.За секунду м-ла в ср.проходит расстояние, численно =ее ср.скорости<v>. Если за это же время она испытает в среднемстолкновений с др. м-лами, то ее ср.длина свободного пробега <ƛ>=<v>\<v>
|
37a Диффузия-неравновесный процесс самопроизвольного взаимного проникновения и перемешивания двух или более различных в-в. В смеси газов причина диффузии-различие в концентрациях отдельных компонентов газов в разн.частях объема.При этом каждый из компонентов смеси направленно переносится из тех частей объема,где ее концентрация больше, туда, где она меньше.Опытным путем установлено (первый закон Фика), что число м-кул dNαкомпоненты α, продиффундировавших через площадку dS за время dt, пропорционально величине площадки dS, промежутку времени dt и градиенту концентрации этого компонента, т. е.
dNα=-Dα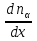 dSdt dSdt
|
37б Если 2соприкасающихся слоя движутся с различными скоростями,то может происходить выравнивание скоростей слоев газов.В ср. импульсы м-кул таких слоев различны – м-кулы более быстрых слоев имеют большие значения импульсов. Переход м-кул из быстрых слоев в более медленный сопровождается переносом импульса упорядоченного движения. Противоположное по характеру действие оказывают м-кулы медленного слоя,перешедшие в быстрый слой,в этом слое возникают тормозящие силы.Суммарный эффект при этом - выравнивание скоростей слоев-внутренним трением. При этом закон, установленный Ньютоном dF=-ὴ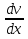 dS.С т.зрения молекулярно-кинет.теории.ὴ= dS.С т.зрения молекулярно-кинет.теории.ὴ=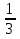 ρƛvcр.арифм. ρƛvcр.арифм.
|
38аБольш.влияние на теплопроводн.оказывает влажность в-ва.При увелич.влажн. теплопроводн.значительно возрастает.Для большинства капельных жидк k теплопроводности с повышением температуры убывает. Для жидкостей его значение находится в пределах 0,08…0,65.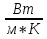 От давления коэффициент теплопроводн. жидк. практическине зависит. Теплопроводн.газовприувелич.температуры возрастает.К теплопровод.газов изменяется в пределах от 0,005 до 0,6 От давления коэффициент теплопроводн. жидк. практическине зависит. Теплопроводн.газовприувелич.температуры возрастает.К теплопровод.газов изменяется в пределах от 0,005 до 0,6 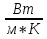 и не зависит од давления.Фурье установил закон- δQ=-X и не зависит од давления.Фурье установил закон- δQ=-X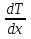 dSdt dSdt
Знак “минус” означает, что тепло переносится от мест более горячих к более холодным.
|
1aМехан.движен.Скорость.Перемещение путь.
1бМехан.движ.Ускорение
2аКинематика вращательного движения
2бз.Ньютона
3аСила взаимод.Сила упругости
3бСила трения
4аВязкое трение и сопротивление среды
4бСила тяжести.Вес
5аДвижение в неинерциальных системах отсчета
5бСилы инерции
6аСила Кариолиса
6бСвязь з.сохран.со св-ми пр-ва и времени
7аКинет.энергия.работа.Мощность
7бПотенциальная энергия.З.сохран полной механ
8аПотенциальная энергия взаимод.с-мы частиц
8бЗ.сохран импульса
9аЦентр масс с-мы частицы
9бЗ.сохран.момента импульса
10аАбсолютн.упругий и неупругий удар
10бПлоское движение тв.тела
11аДвижение центра масс тв.тела
11бВращение тв.тела вокруг неподв.оси
12аМомент инерции.Т.Штейнера
12бКинет.энергия вращающ.тв.тела
13акинет.энергия тела при плоском движен
13бЗ.всемирного тяготения
14аГравитацион.поле.Принцип эквивалентности
14бВиды механ.колебаний и динам.у-я
15аГармонич колебания
15бМатем.и физ.маятник
16асложение взаимно перпенд.колебаний
16бЗатухающие колебания
17аВынужденные колебания
17бУпруг.волны в средах.Попереч.и прод. волны
18аУ-е бегущей волны
18бПринцип суперпоз.волн.Групповая скорость
19аЛинии и трубки тока.Неразрывность струи
19бу-е Бернулли
|
20аЛаминарное и турбулентное течение
20бДвижение тел в жидк.и газах.У-е Стокса
21аДавление газа ст.зрения молек-кинет теории
21бу-е состояния идеального газа
22амолек-кинет смысл абсол.теммпературы
22бЧисло степен.свобод.З.равнораспред.энергии
23аЭнергия.Внутр.энергия.Кол-во теплоты
23б1ое начало термодинамики
24аРабота соверш.газом при измен.обьема
24бТеплоемкость идеальных газов
25аТермические коэффициенты и их связь
25бприменение 1ого начала термодин
26ау-е адиабаты
26бПолитропические процессы
27аРаспределение Максвелла
27ббарометрическая формула
28аРаспределение Больцмана
28бПодьемная сила
29аОбратимые и необратимые процессы
29бТепловая машина
30ацикл карно
30б2 начало термодинамики
31аэнтропия как ф-я состояния термодин с-мы
31бматем.формулир.2 нач.термодин.
32астатистич.смысл и св-ва энтропии
32бИзменение энтропии в процессах идеаль.газа
33а3начало термодинамики
33бРеальные газы.Силы межмолекул взаимод.
34аУ-е Ван-дер-Вальса
34бИзотермы у-я Ван-дер-Вальса
35бИзотермы реального газа
36аИзотермы жидкости
36бЯвление переноса.Ср.длинна свобод.пробега
37аДиффузия в газах.З Фика
37бЯвление внутр.трен.газа.З Ньютона
38аТеплопроводность З.Фурье
|
|
|
|
 Скачать 230.67 Kb.
Скачать 230.67 Kb.